EE 421L Final Project
Project (NOT a group effort) – design a non-inverting buffer circuit that presents less than 100 fF input capacitance to
on-chip logic and that can drive up to a 1 pF load with output voltages greater than 7V (an output logic 0 is near ground
and an output logic 1 is greater than 7V). Assume VDD is between 4.5V and 5.5V, a valid input logic 0 is 1V or less, a valid
input logic 1 is 3V or more. Show that your design works with varying load capacitance from 0 to 1 pF. Assume the slowest
transition time allowed is 4 ns.
Part 1 Preparation:
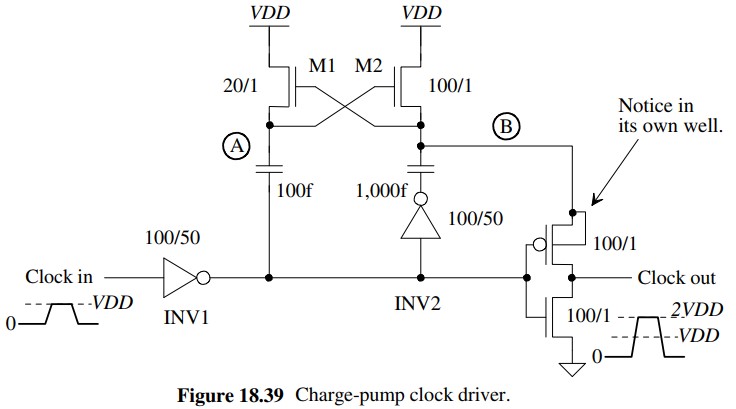
As preparation for this project, we were directed to Chapter 18 in our CMOS book, and told we could follow the charge-pump clock driver example found in Figure 18.39 (seen below) to design our project. This example is a non-inverting device that provides an output up to 2VDD, both of which tie in to the requirements of this project. Having the output reach up to 2VDD is essential for this project as we are allowed a VDD of 4.5V to 5.5V but can only get a logic 1 output if our output voltage is greater than 7V, even if we use the lowest VDD option (4.5V) the output voltage should be able to get to 9V exceeding the threshold for a logic 1 output.

Although this example is extremely useful, I could not just copy this figure as is. With the restrictions given, I had to calculate a decent size for each device within it and ensure that they all fit well together while maintaining the crucial 2VDD output.
Circuit Limitations:
Part 1 Procedures:
Input Inverter Creation and Simulations:
I started at the beginning of the circuit, specifically with INV1, to figure out a decent size that would maintain the limitation on the input capacitance.
I started by assuming the inverter was using the minimun length (0.6um) then solving for the maximum width of the PMOS and NMOS devices. Right before I solved for the width though, I realized that I completely ignored the values in the example. I figured this project wouldn't be easy enough that the answers were just given to us but I wanted to check and make sure, so I started testing the given values for the inverter from Figure 18.39 (right side of the line).

As the book used the 50nm CMOS process, I had to convert the given values into the C5 CMOS process by multiplying 0.6um. However when I solved for Cin, I found out that the values from the book were way too large for this project—ending up with an input capacitance of 202.5fF—and continued solving for the maximum widths.
The next part of this solution depended on whether the NMOS and PMOS widths should be the same or if the PMOS should be twice as large as the NMOS. Testing out both methods though, showed that it did not matter as they still provided the same input capacitance of 99.9fF.

While 99.9fF is less than 100fF, it felt too close to comfort for me and I wanted more of a buffer between the input capacitance limit and my actual input capacitance. This hesitance was also due to thinking of future projects and knowing that, were this to be built with hardware, there may be some physical issues that could push the input capacitance over the specified limit.
As I found out above, any smaller width would work to stay within the input capacitance limit, so I turned to some familiar values that I have used for my inverters all semester: Wp = 24um and Wn = 12um. I decided on the PMOS width being twice as large as the NMOS width as, not onlyl were those the given values in class, but I felt that design would work better with the overall circuit rather than a smaller square. So, deciding on those values, I had to actually check to make sure they would keep the input capacitance below 100fF. And they did, the input capacitance with those values ended up being 81fF which is less than 100fF and gives plenty of room for error to work around.

Now that I decided on the size, I quickly created the schematic and symbol for the inverter with Cadence.
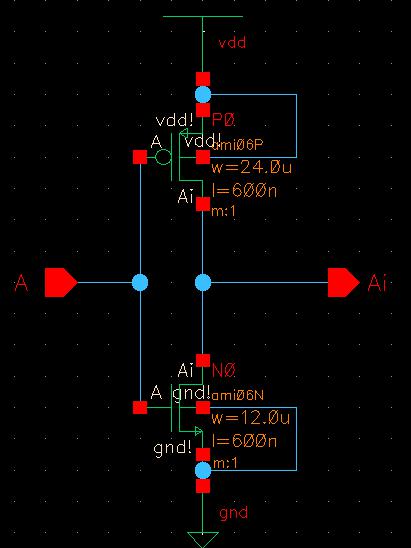
To ensure the inverter was working properly, I conducted simulations with three possible VDD values: 4.5V, 5V, 5.5V.

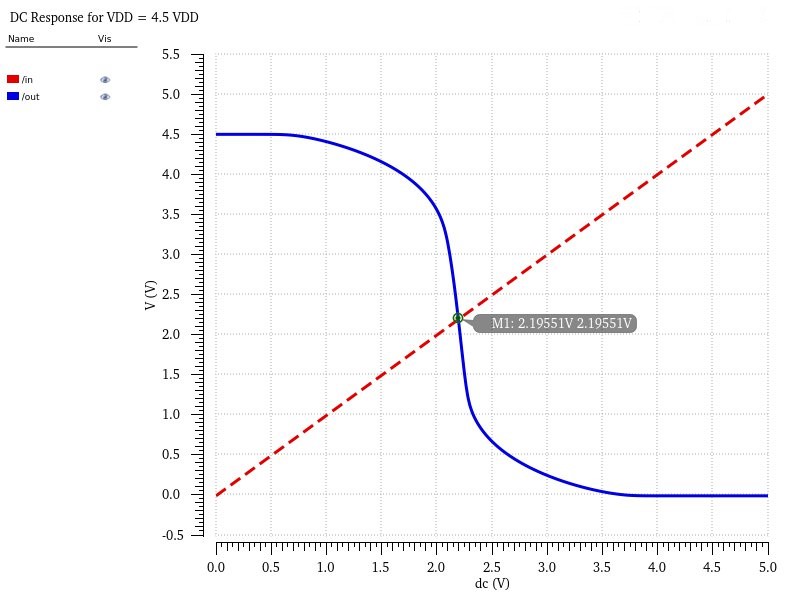
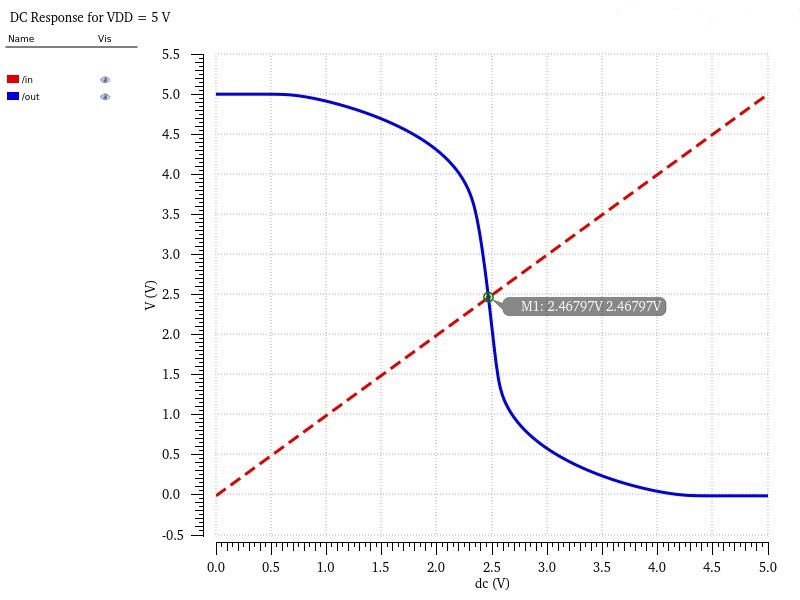
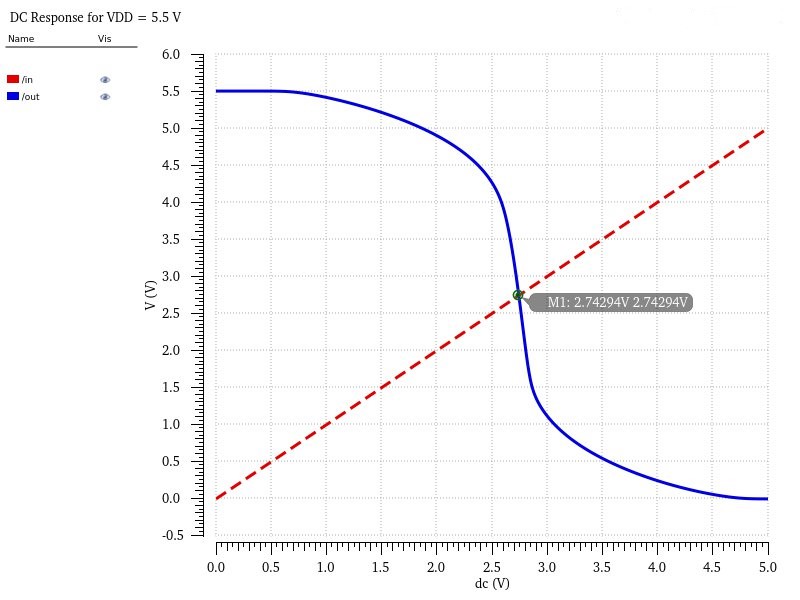
A key thing to note from these is that the switching point changes depending on the provided VDD, however they are all within the expected range of ~2.5V and would not interfere with the input logic requirements for the project. I also used this same inverter for INV2.
Output Inverter Creation:
After completing the requirement for the input capacitance, I moved on to satisfying the output capacitance. For this final inverter—the inverter that produces the output—I needed to ensure that it would keep the entire device within the 4ns transition frame. Again, I was assuming the minimum length (0.6um) was being used for the inverter so I had to solve to the maximum widths of the NMOS and PMOS again, this time using the time delay formula. For this formula, I also needed a resistance value which I chose to be 1k. Other than this value being given to us in class (through this helpful note), I felt that 1k would be the easier value to deal with as it could quickly cancel out part of the load and remove a few orders of magnitudes.

Here, I was able to obtain the inverter widths to be Wp = 24um and Wn = 12um which ended up being the same as the first inverter for this non-inverting buffer.
I also calculated my expected time delay at this time, using the 1k resistance value mentioned earlier. While the 2.2RC equation is the intended one to use, providing a delay of 2.2ns, I also wanted to see how much the delay could vary using the 0.7RC equation.

"Capacitor" Creations:
With all the inverters good to go, it's time to move up the circuit to the capacitors. Both capacitors will be created from NMOS devices in strong inversion rather than a poly-poly capacitor or an actual capacitor. The use of strong inversion is better than a poly-poly capacitor as seen by their resistance per square, with a poly-poly capacitor using 900aF/um^2 compared to the 2500aF/um^2 from an NMOS with the larger having better capacitance.The more important capacitor is the right one as that assists in obtaining the correct output so it must be larger. This capacitor also needs to be shared with the 1pF capacitive load that will be applied outside this non-inverting buffer, as they both feed directly into the output.
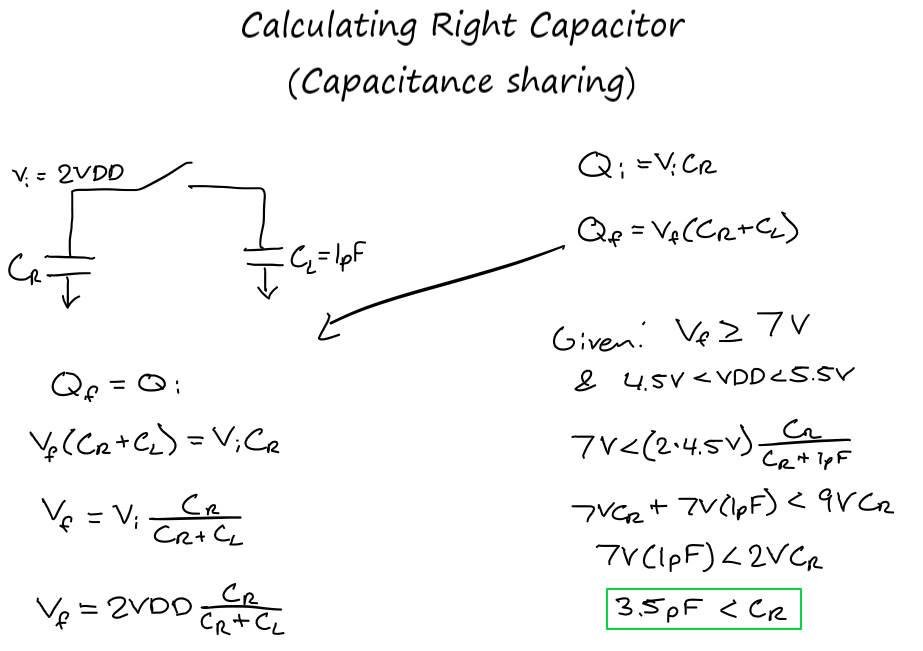
Since this capacitor needs to be larger than 3.5pF, I turned to digikey to help me select the best capacitance. I began my search at 5pF due to knowing the tolerance range could vary drastically depending on theh capacitance and I did not want to change picking a capacitor within the 4pF range and having it's tolerance dip below 3.5pF at any point. By starting at 5pF and looking upwards, I was ensuring the tolerance would not be an issue, allowing the NMOS to stay in strong inversion at all times.
| Capacitance range (pF) | Best Tolerance | Best Price |
| 5-5.9 | ±0.05pF for 5.6pF range: 5.55 - 5.65 | $0.00138 for 5.6pF |
| 6-6.9 | ±20% for 6.8pF range: 5.44 - 8.16 | $0.00138 for 6.8pF |
| 7-7.9 | ±0.05pF for 7pF range: 6.95 - 7.05 | $0.00175 for 7pF |
| 8-8.9 | +20%,-15% for 8pF range: 6.8 - 10 | $0.00126 for 8pF |
As seen on the table above, I found the best price to be $0.00126 for an 8pF capacitor with a decent tolerance range. Once I picked my capacitance, I had to figure out the best NMOS size for it.

I ended up with WL=3200um^2 which could be split in two ways: W=80um, L=40um or W=64um, L=50um. So I made a chart comparing each option.
| W=80um L=40um | W=64um L=50um |
|
|
And the results of this led to me picking W=80um, L=40um for the NMOS.
Looking at the other capacitor, it's not as important since it does not impact the output so it could be much smaller. As it does not matter, I chose to use the capacitance it has in Figure 18.39, 100fF but

While this could also have multiple options—W=20um & L=2um, W=10um & L=4um, W=8um & L=5um—I chose to go with W=10um & L=4um as that had a closer W/L ratio (2.5) to the rest of my devices than the other options.
Last but not leasat, the top two NMOS devices. I chose to keep those the same as Figure 18.39 as it worked just fine when I tried it and I saw no reason to change something that worked.
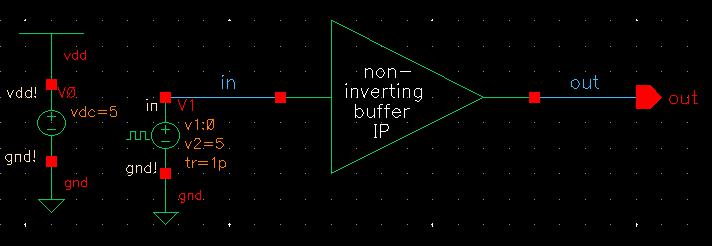
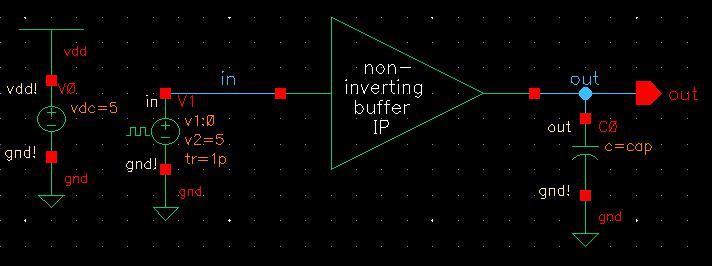
Complete Non-Inverting Buffer Schematic and Symbol:
So my final circuit and symbol came out as the following.
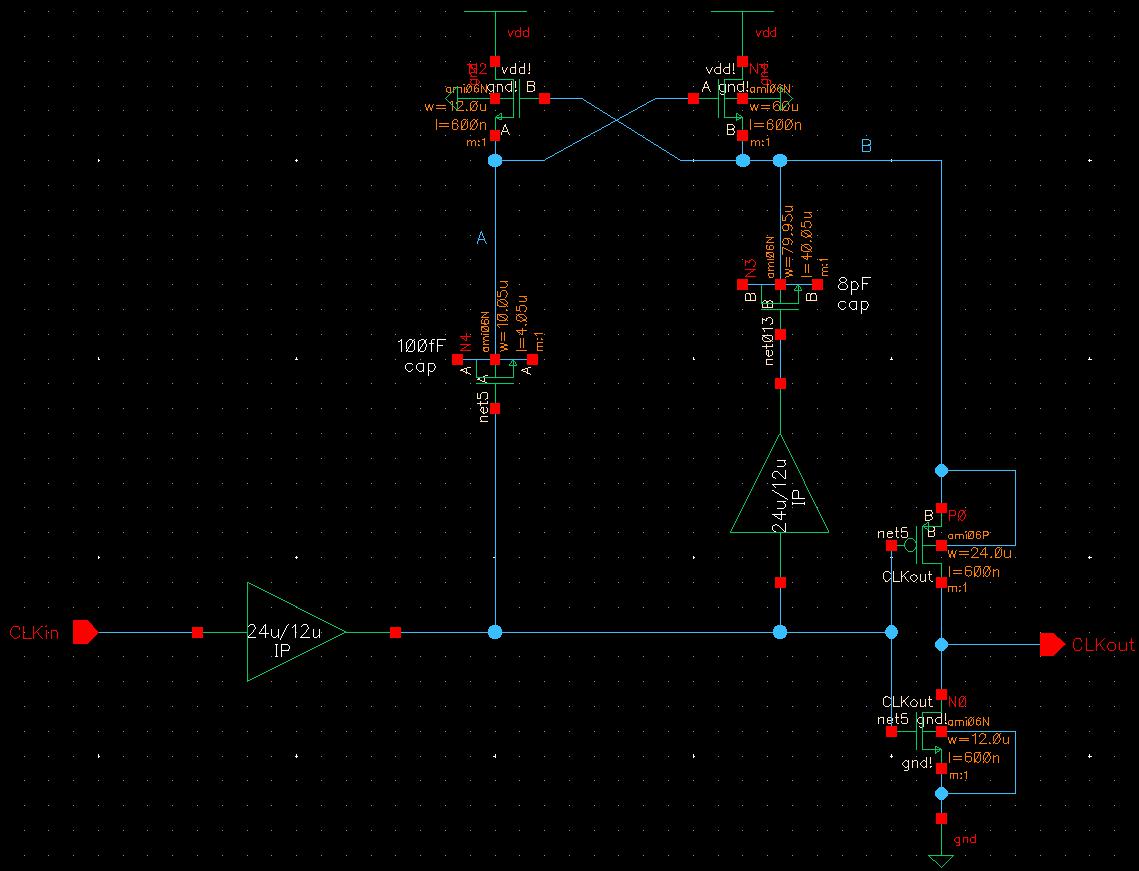
Non-Inverting Buffer Simulations:
Now that the buffer is complete, I can begin testing it with simulations to ensure it works properly.
The first set of simulation tests is to see if net B actually becomes 2VDD as expected. The simulation is a simple input pulse from 0 to 5V and checks if B changes from VDD to 2VDD using three different VDD possibilities: 4.5V, 5V, and 5.5V.
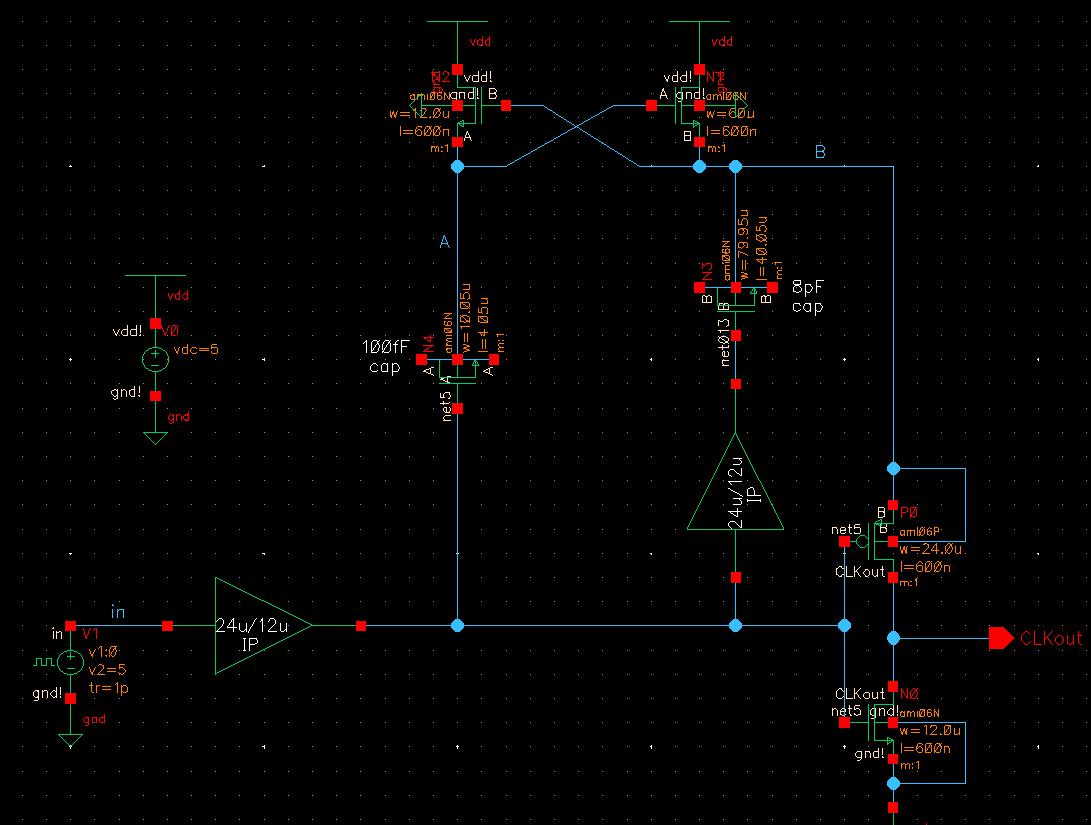
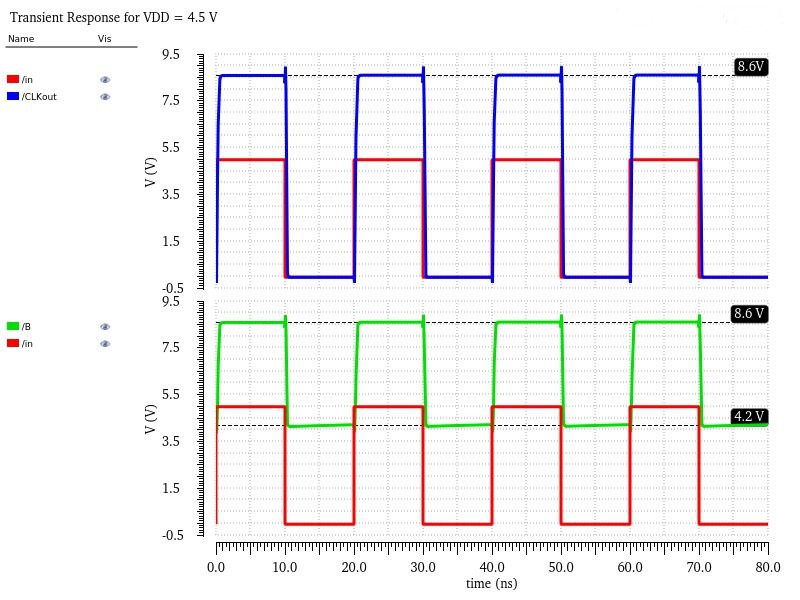
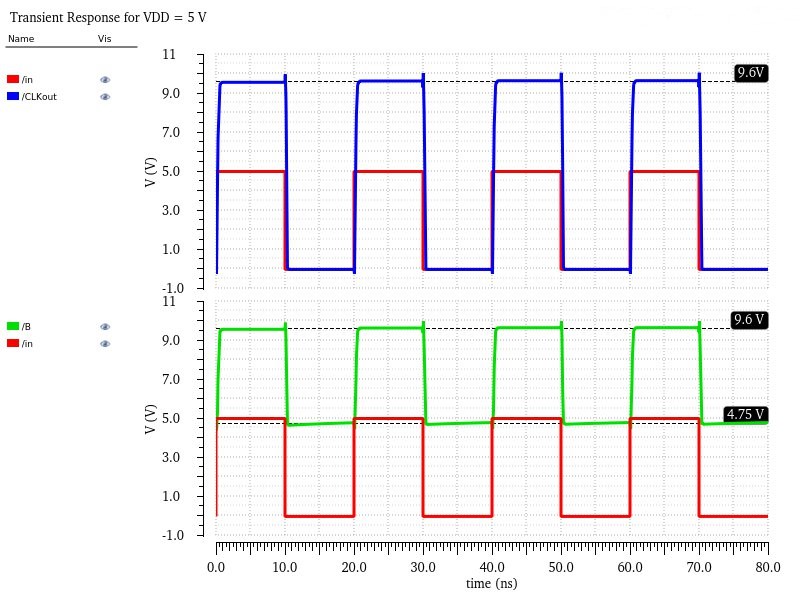
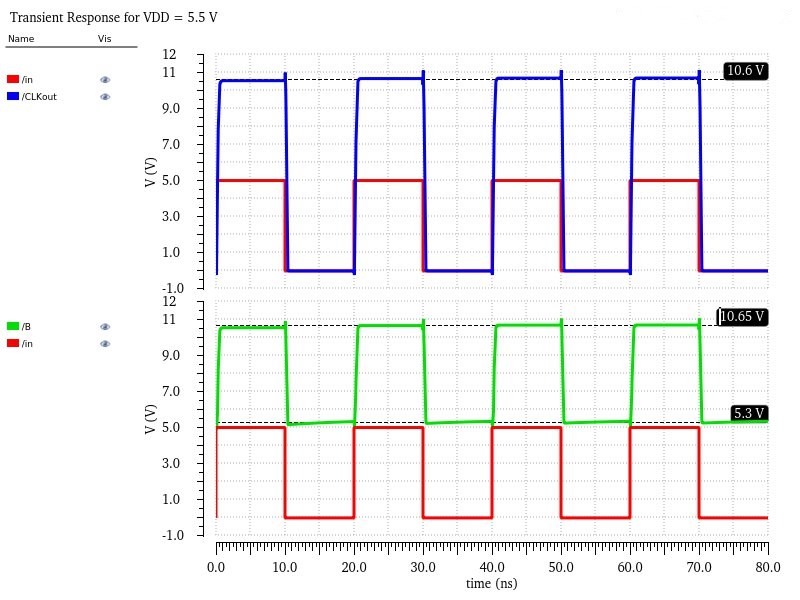
With each test, I noticed B actually starts at ~0.25V below the provided VDD but it does double the initial value, displaying that it works as intended. I believe the misalignment in VDD is due to some resistance between net B and the input lowering the voltage before it can reach B. I also noticed that it's only about a 5% error range, which matches the tolerance levels of the capacitor I picked, so that may be the cause as well.
The next set of simulations is testing the full non-inverting buffer with no load.
I started this set of testing changing the input voltage from 0 to 3V to make sure that the output is a logic 0 at or below 1V and a logic 1 at or above 3V.
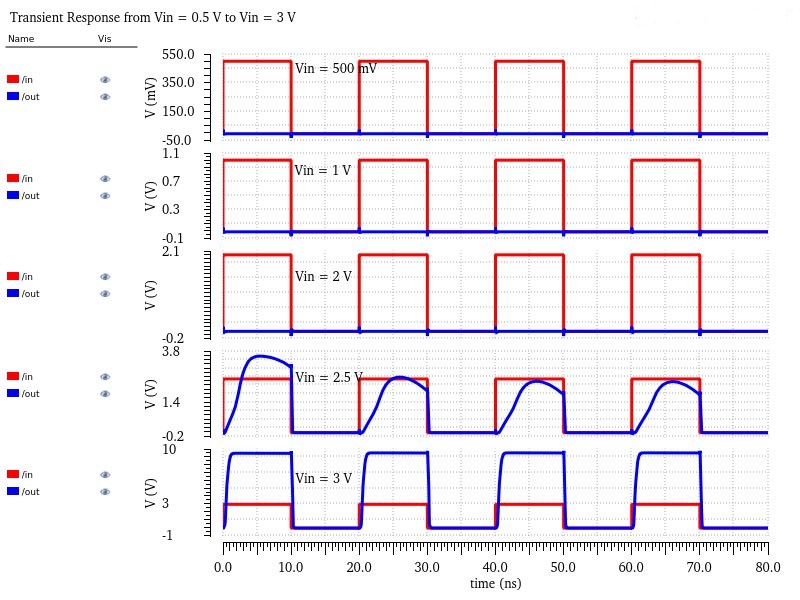
I also tested input voltages at 2V and 2.5V to demonstrate that the output is unsteady during the switching point, hence why there is no logic 1 or 0 between 1V and 3V.
Then, I again changed the VDD from 4.5V to 5V to 5.5V to demonstrate it working through the full VDD range.
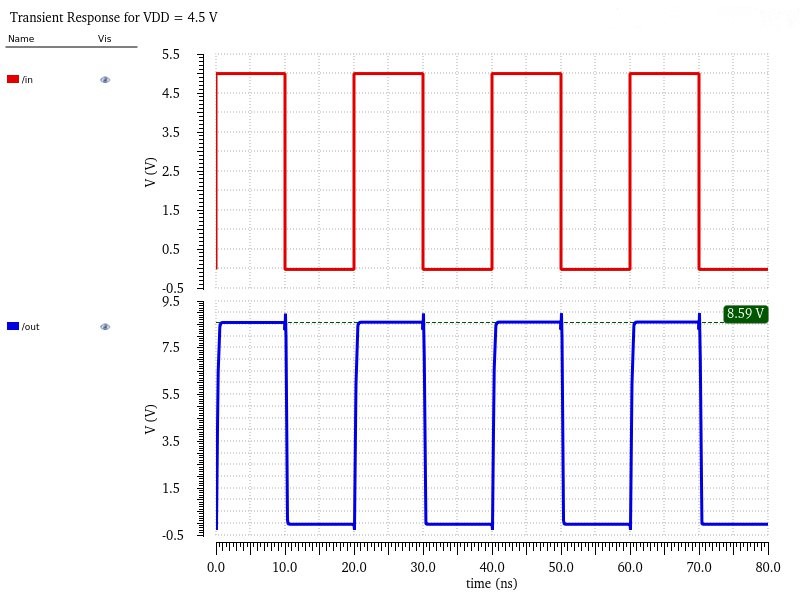
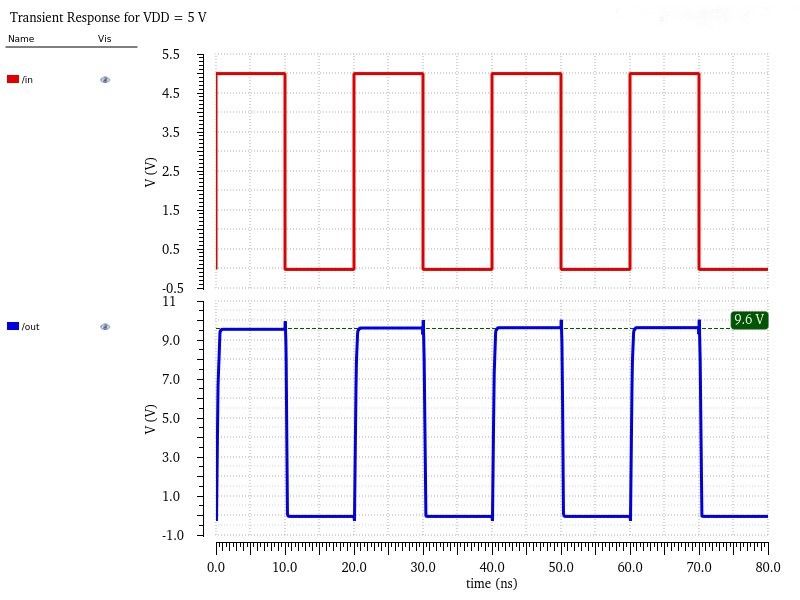
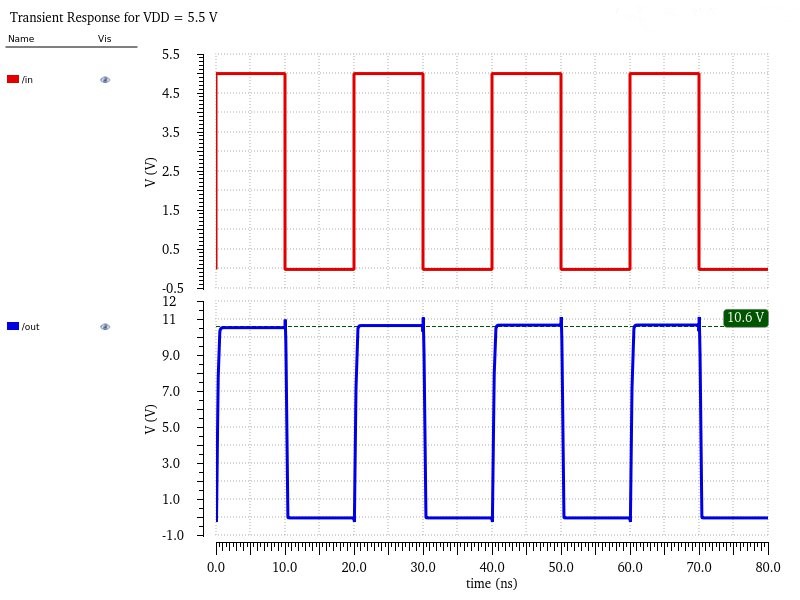
Finally, the last simulation for no node is showing the rising and falling times at the highest possible VDD (5.5V) as if the total delay is still within 4ns at the highest VDD then the lower VDDs will safely be within it.
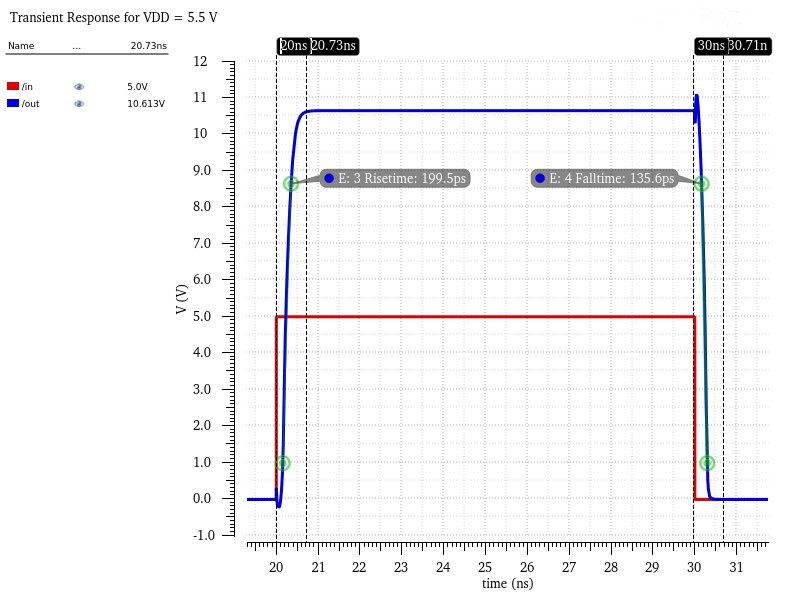
According to Cadence's rise/fall time calculations (which only account for 20%-80% of the edge) the total delay (199.5ps+135.6ps) is 0.3351ns which is well within the 4ns range. You can also see from my markers, which is closer to the true 100% edge, that the delay is ~0.7ns, which again is well within the 4ns limit.
Last but not least are the simulations for the full non-inverting buffer with a varying capacitive load that maxes out at 1pF.
Again, I ran tests for VDD being set to 4.5V, 5V, and 5.5V but now that a capacitor is involved I created a parametric analysis that increases the capacitor from 0 to 1pF in 5 steps. So the following graphs display the transient response of the different VDDs when the capacitor is at 0, 200fF, 400fF, 600fF, 800fF, and 1pF. I have also included the rise and fall times, supplied by Cadence, for all the 1pF and 0 loads to show how much the delay varies as the load increases. I did not include any in-between capactors as they all fall between 0 and 1pF so if those are safely within the 4ns limit then all of them are.
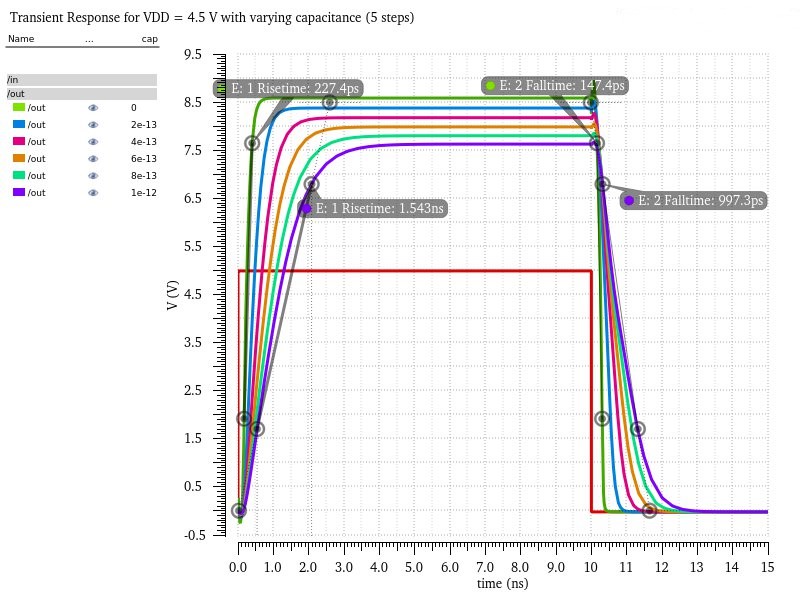
The total delay when VDD = 4.5V for no load is 0.3748ns and the total delay for 1pF is 2.5403ns, which is close to what was predicted in the hand-calculations.
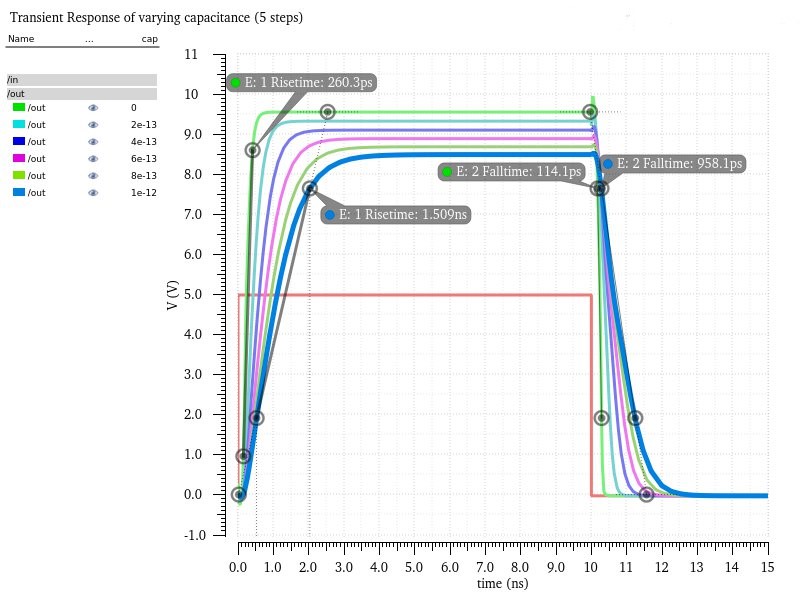
The total delay when VDD = 5V for no load is 0.3744ns and the total delay for 1pF is 2.4671ns, which is lower than when VDD = 4.5V.
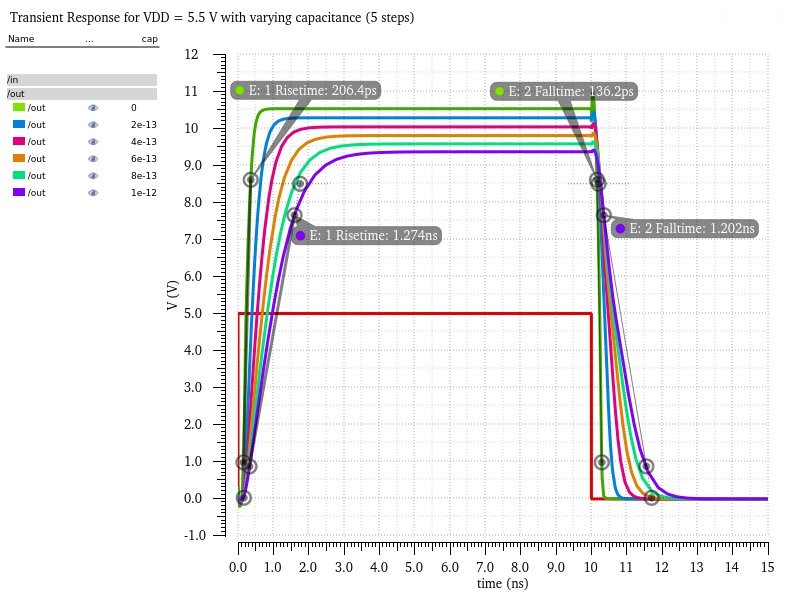
The total delay when VDD = 5.5V for no load is 0.3426ns and the total delay for 1pF is 2.476ns.
So all the delays are safely within the specific 4ns limit and are close to the predicted 2.2ns delay from the hand calculations.
This final graph is showing off an output of logic 1 (with vin = 5V) and an output of logic 0 (with vin = 1V) to demonstrate that the output logics are still intact once the load was added.
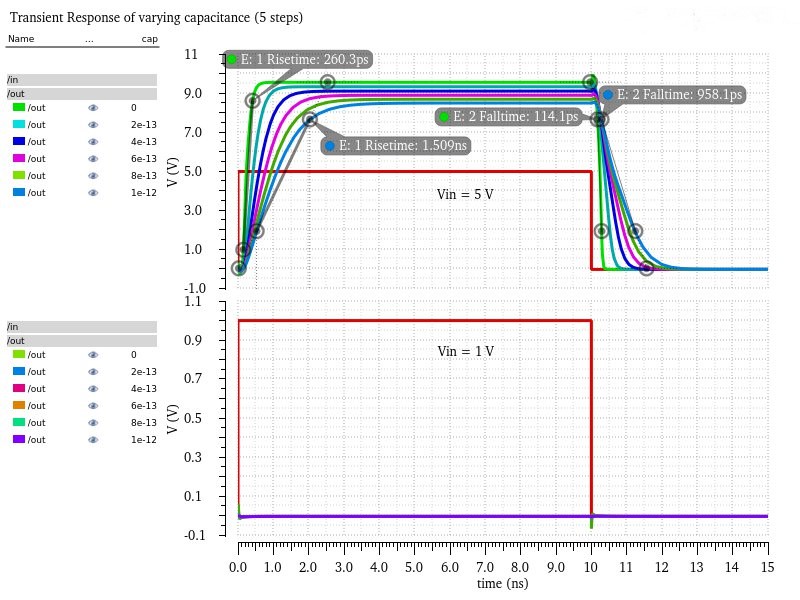
This concludes the first half of the project, all work completed in the first half can be found in project_lab_pt1_IP_F23.
Return to EE421L Final Project Index