Lab 5 – EE 420L
Authored by: Daniel Senda
Email: sendad1@unlv.nevada.edu
Spring 2019
Due: 03-13-2019

1) Introduction

The purpose of this lab is to introduce the student to operational amplifier integrators. The student is required to calculate characteristics associated with integrators as well as physically test integrator circuits. In addition, the student is required to design an integrator circuit to fit given requirements.

2) Pre-Lab Description

The pre-lab required the student to do the following before proceeding with lab:

- Watch the op-amp III video and read op-amp_III.pdf review.

- Simulate the circuits given in the op-amp_III.zip file and understand operation.

- Read the entire lab write-up before going to class.

3) Description of Lab Procedures

This lab utilized the LM324 operational amplifier (op-amp). The datasheet can be found here.

The student was asked to answer the following questions assuming V_CC+ = +5V and V_{CC –} = 0V.

- Calculate the frequency response of the following circuit. Ensure you show your clear hand calculations.

Schematic of integrator circuit:

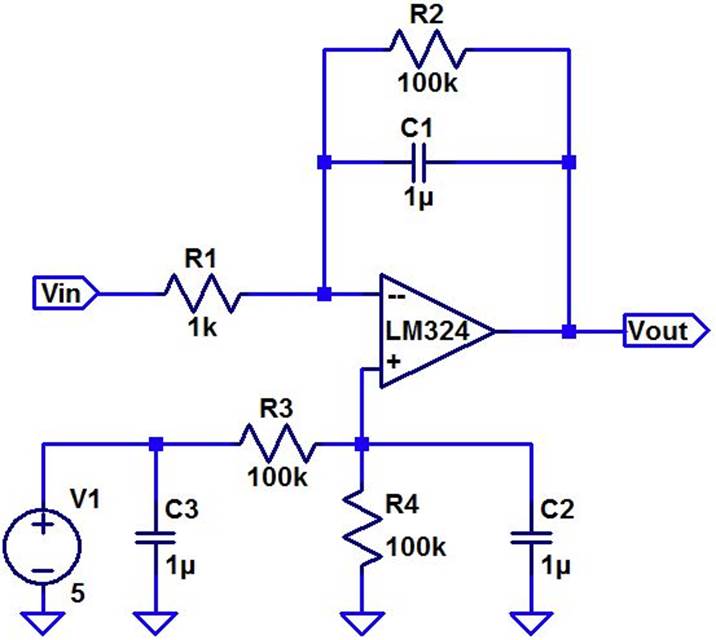
The following hand calculations show how to calculate the frequency response of the

this circuit.

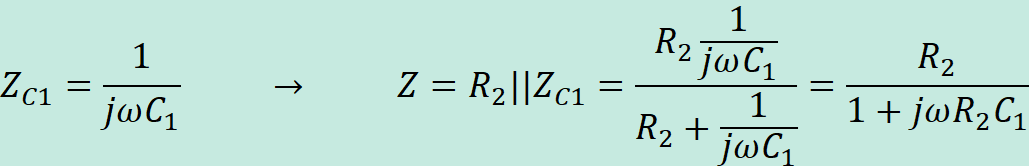
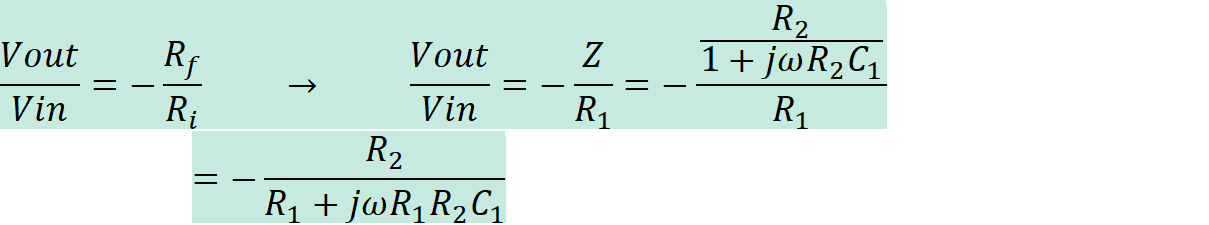
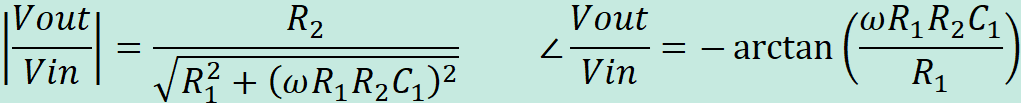
- What can you neglect to simplify the calculation?

The student can neglect R2 in order to simplify the calculation. This can be done because R2 is much bigger than R1, so removing R2 from the equation will have a small effect on the results as can be seen below.

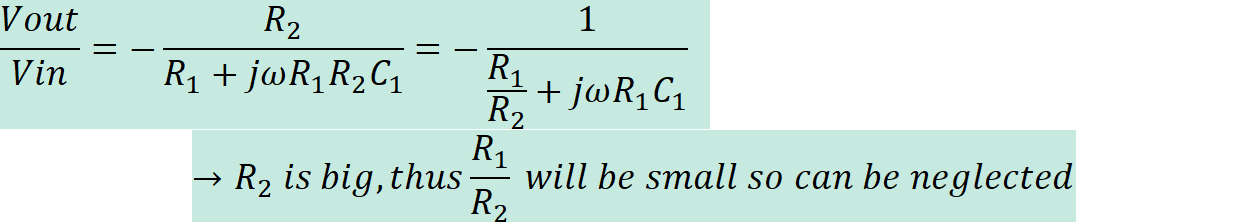
- Does the circuit work if you remove the 100k? Why or why not?

If the 100k resistor is removed from the circuit, it should work but since the op-amp is not ideal there will be issues. The feedback loop is no longer present affecting the offset, so the output signal may rail if the input amplitude is too large.

- Does the 100k have much of an effect on the frequency response?

The 100k resistor does not have much of an effect on the frequency response of the circuit. The reason for this is because the value of R2 is big compared to R1, so it’s almost as it was an open through R2 (infinite resistance, which implies no resistor).

- Verify your calculations with experimental results.

Waveform of circuit with R2 in place:

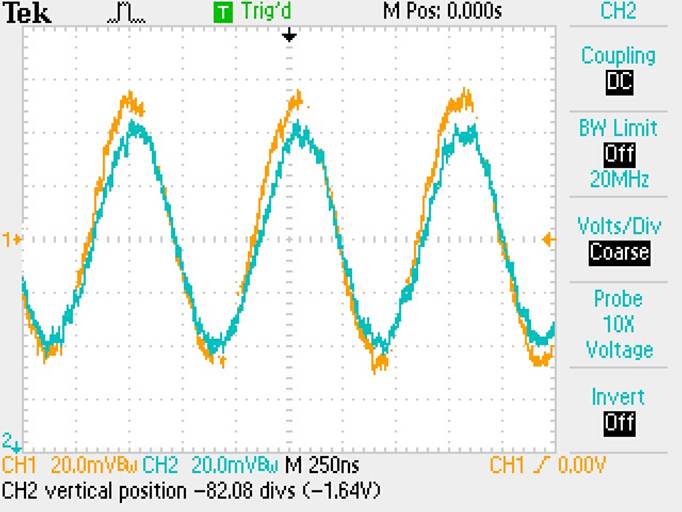
As can be seen, there is a DC offset of about -1.64V on the output signal.

Waveform of circuit without R2:

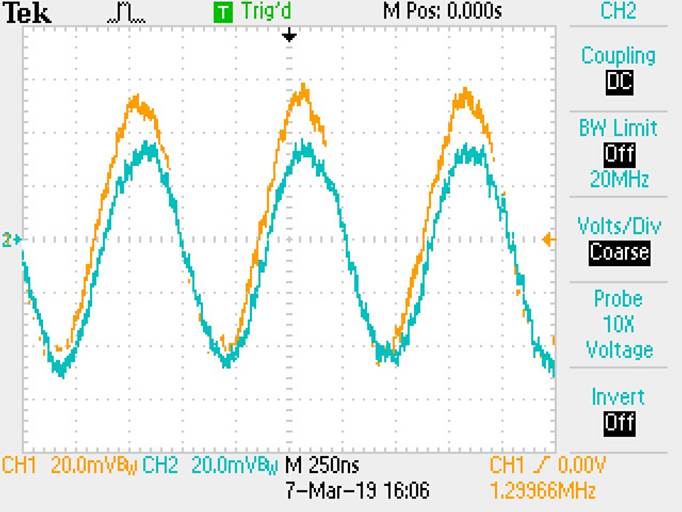
If R2 is removed from the circuit, the DC offset is removed from the output signal as demonstrated by the oscilloscope.

This results show how the DC offset changes depending if R2 is present or removed.

- Show, at the unity-gain frequency of the integrator, that the input and the output have the same peak values.

The following is the calculations for unity frequency.

Unity-gain frequency circuit schematic:

Unity gain frequency waveform results:

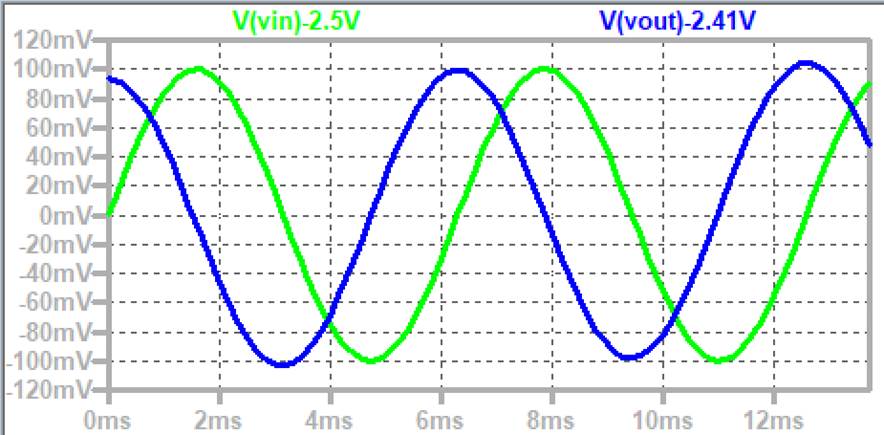
As can be seen from the waveform, the amplitudes of Vin and Vout are the same.

- Is the phase shift between the input and the output what you expect? Why or why not?

The phase shift between the two signals is -90 degrees, which is what was expected by the student. The reason it was expected is because capacitors are known to cause a -90 degree phase shift in a AC signal.

The last part of the lab had the student design, simulate, and build a square-wave to triangle-wave generation circuit. The following instructions were given.

- Assume the input/output frequency is 10 kHz and the output ramp must swing from 1 to 4 V centered around 2.5 V.

- Show all calculations and discuss the trade-offs (capacitor and resistor values, input peak, min, and average, etc.)

The following is the calculations that were made to design the required circuit.

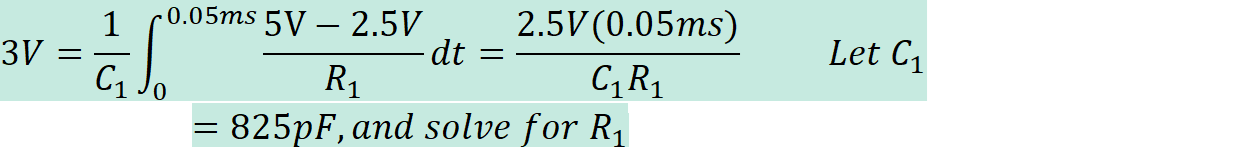
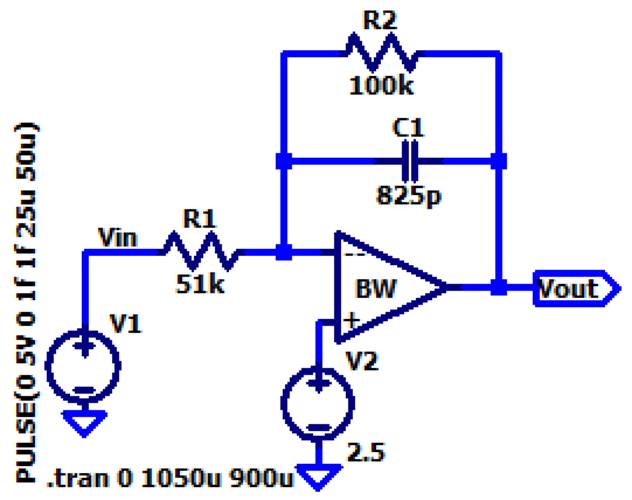
Designed circuit schematic:

Designed circuit simulation waveform:

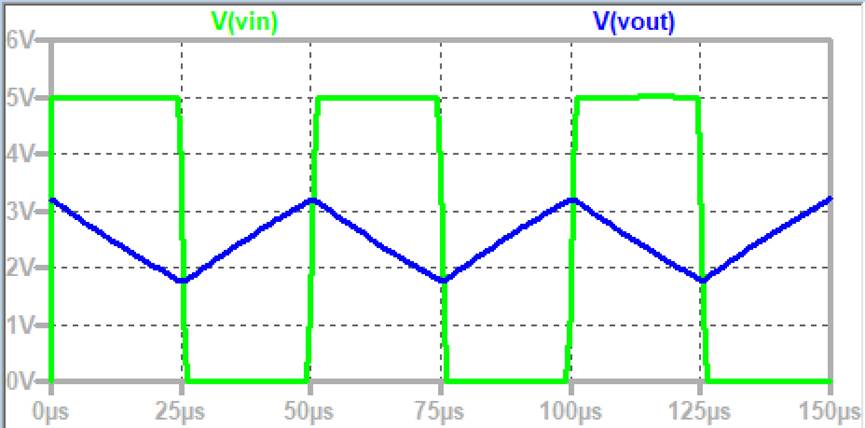
The waveform shows that the output is swinging in-between 1 to 4 volts. In order to get a swing of exactly 1 to 4 volts, the R1 value should be reduced to 25k ohms.

The circuit was then created in the breadboard and the following waveform was generated. As can be seen, the output is close to the design requirements. It does have some unwanted noise, but is there because the built circuit is not ideal.

Oscilloscope waveform of built circuit:

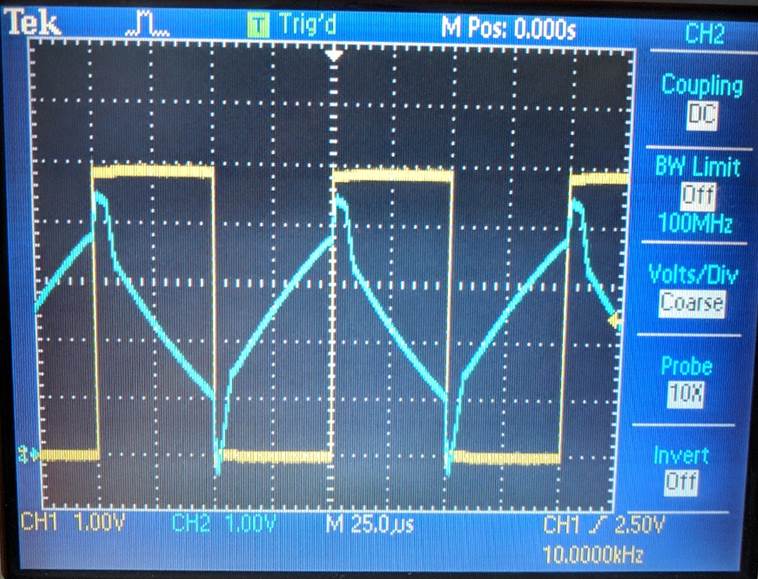
Some of the trade when designing this circuit is component values. If a smaller resistor is what is available, then a bigger capacitor value will result from the calculation. From experimental experience when building this circuit, it seems that a smaller capacitor gives cleaner results. Thus, if you have a bigger capacitor because of small resistor value, the output will have a bit more noise. Also, the designer needs to keep in mind that the peak values of the triangle wave needs to stay between 0 and 5 volts, or else the signal will rail.

This concludes lab 5. (Lab was backed-up on an external drive)

Additional Links

→ Return to listing of lab reports
→ Daniel’s CMOS homepage
→ Dr. Baker’s CMOS homepage