Lab

EE 420L Engineering Electronics II Lab - Lab 4

Nha Tran
02/26/2015

NSHE: 2000590233

trann4@unlv.nevada.edu

Again, this lab will utilize the LM324 op-amp (LM324.pdf).

For the following questions and experiments assume VCC+ = +5V and VCC- = 0V.

Estimate, using the datasheet, the bandwidths for non-inverting op-amp topologies having gains of 1, 5, and 10.

From the data sheet of the LM324 Op-amp we can see that the unity gain frequency is 1.3 MHz. The equation to find the Bandwidth (BW) is BW = Fun/Aol, for the gain of 1, 5, and 10 we have the following Bandwidth.

Gain	Bandwidth
1	1.3 MHz
5	260 kHz
10	130 kHz

Experimentally verify these estimates assuming a common-mode voltage of 2.5 V.

Your report should provide schematics of the topologies you are using for experimental verification along with scope pictures/results.
Associated comments should include reasons for any differences between your estimates and experimental results.

Since we know the gain for the non-inverting topology is gain = 1 +(R2/R1) to get a gain of 1 we build a circuit in lab similar to the one below using ltspice.

non-inverting topology: Gain = 1
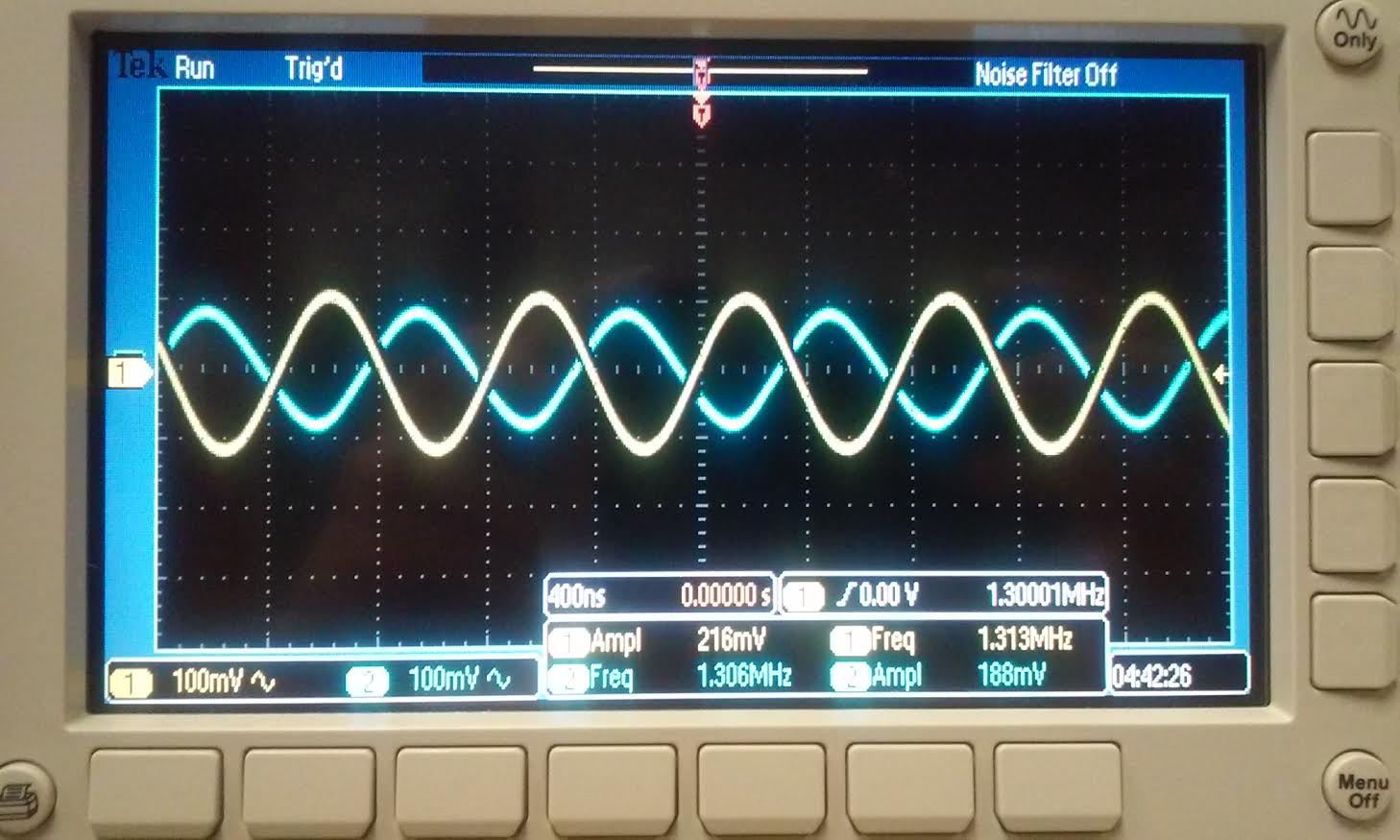
To get a gain of 1 we did not have any resistors; we just put a wire between Vout and Vminus, as you can see from the scope reading the amplitude of the input is 216mV with a 100mV input from the signal generator, and the output's amplitude was 188mV. The value of the input and output is close enough that we can say that the gain is approximately 1. Also from the scope reading you can see that the input frequency is 1.3MHz. Bandwidth = 1.3MHz

non-inverting topology: Gain = 5 For the gain of 5, we used the resistor of 4k and 1k since the equation for gain is Aol=1+R2/R1. The input amplitude was 96 mV, while the output was 464mV. The ratio is approximately 5, so we can say that the gain is 5. Our input frequency was 110 kHz. Bandwidth = 110kHz

non-inverting topology: Gain = 10 For the gain of 10 we used a 9k and 1k resistor our input was 152mV, and the output was 1.17 V. The input frequency was 40kHz. Bandwidth = 40kHz

As you can see from the table below, the theoretical bandwidth differs from the experimental bandwidth because from our estimation of the theoretical value the Vcc input was 30V. However, for the lab experiment we only used a 5V Vcc. The value that the datasheet gives us is just a typical rating of GBP for all the op-amp that was produced at the time. the datasheet gave us a 1.3MHz GBP, that value was just a typical value but in reality it can varies. LM324 was design for low power, they can get alot of unwanted noise and corssover distortion from cicruits. Their frequency response and GBP is much less when the VCC is less than 30V, which was the case in our lab. Also we did not factor in the noise gain of the op-amp that we are using.

Gain	Theoretical	Experimental
1	1.3 MHz	1.3 MHz
5	260 kHz	110 kHz
10	130 kHz	40 kHz

Repeat these steps using the inverting op-amp topology having gains of -1, -5, and -10.

The gain for a inverting op-amp is Aol = -R2/R1. The unity frequency from the datasheet is 1.3Mhz. the equation for BW = Fun/(1+Aol). The theoretical bandwidth that we should get from the datasheet is

Gain	Bandwidth
1	650 kHz
5	217 kHz
10	118 kHz

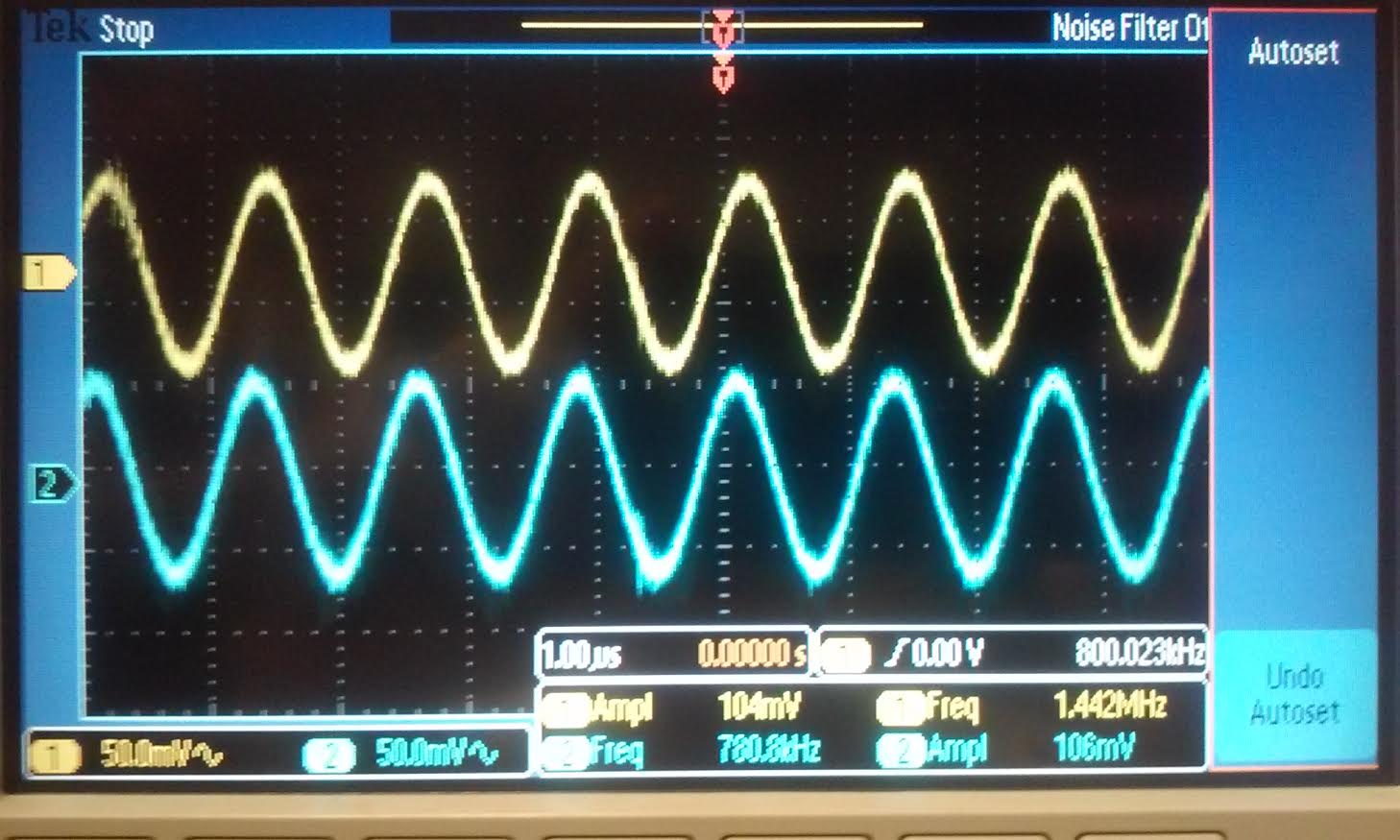
Inverting gain = 1: similar to the non-inverting op-amp circuit except this time we just have the signal goes to the Vminus and VCM goes to Vplus. with our input of 104mV we got a 106mV output when the BW is 780kHz. Again similar to the above schematic we did not use any resistor for a gain of 1.

Inverting gain = 5: This time our input was 100mV, the output was 528mV, indicating that the gain is 5. the bandwidth that we were able to achieve this was 100kHz. This time we used a 10k and 51k resistor for our R1 and R2.

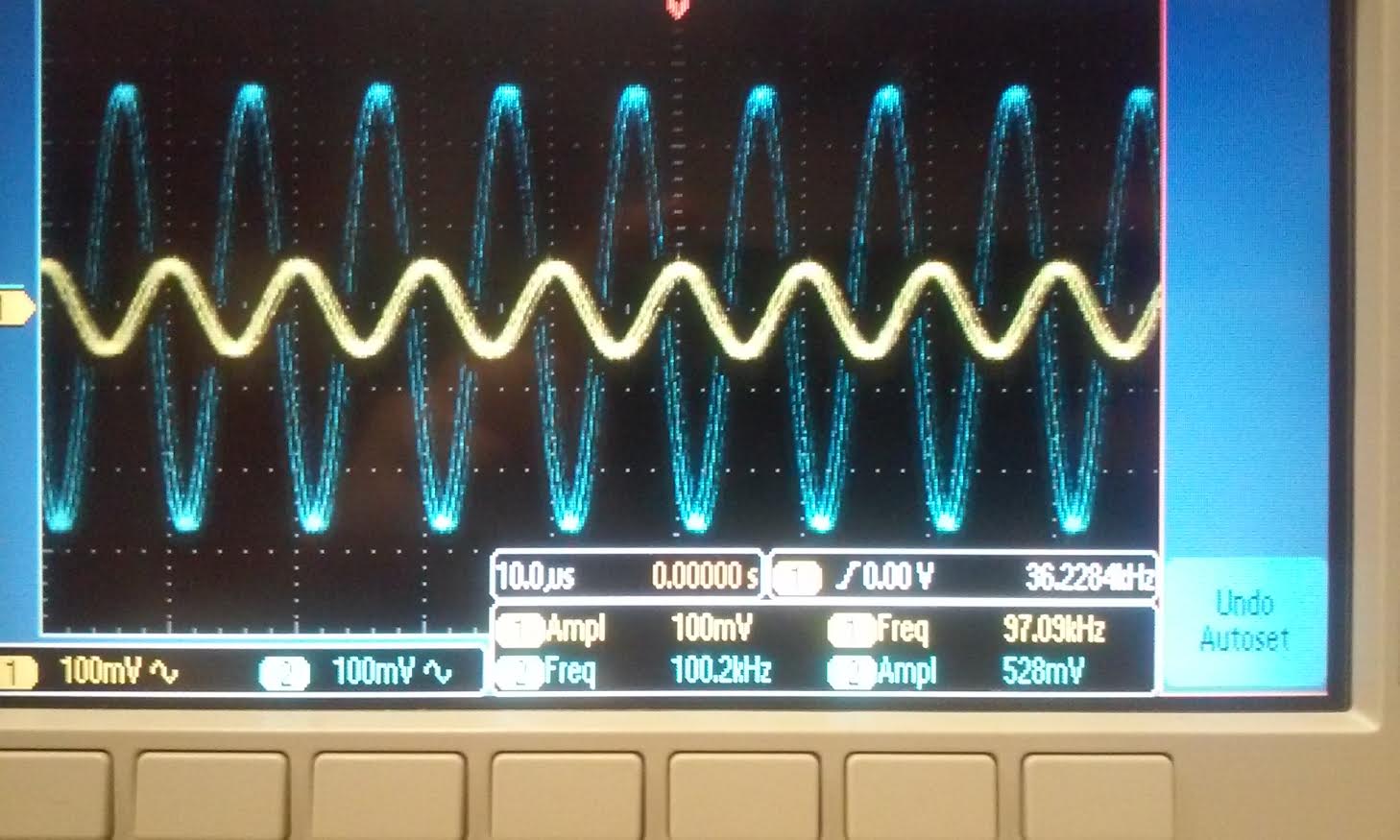Inverting gain = 10: For a gain of 10 we used a resistor of 10k and 100k, our scope input was 96mV our output was 990 mV indicating a gain of 10. This was achieved with the bandwidth of 60kHz.

As you can see from the table below, the theoretical values differs from the experimental values. The same explanation that i used for the non-inverting op-amp above.

Gain	Theoretical	Experimental
1	650 kHz	780 kHz
5	217 kHz	100 kHz
10	118 kHz	60 kHz

Design two circuits for measuring the slew-rate of the LM324. One circuit should use a pulse input while the other should use a sinewave input.

Provide comments to support your design decisions.
Comment on any differences between your measurements and the datasheet’s specifications.

The slewrate that the datasheet gives us is 0.4 V/us, again this is the typical value it will probably not match our experimental value.

For the slewrate using a pulse wave we just choose the non-inverting topology with no resistor value. We made a measure of the rise time using the scope's measure option. And to measure the 10% and 90% voltage we did an eyeball of the output. We adjust the cursor to the location that we think was 10% and 90% respectively. As you can see from the scope reading the rise time is 220.8 ns. and the deltaV = 86mV. We can use the equation slewrate (SR) = deltaV/RiseTime, for our experiment the SR = 86mV/220.8ns = 389mV/us = 0.389V/us.

For the sine wave we use the same topology without any resistor also. we made the same measurement and SR=600mV/2.472us = 243mV/us = 0.243V/us.

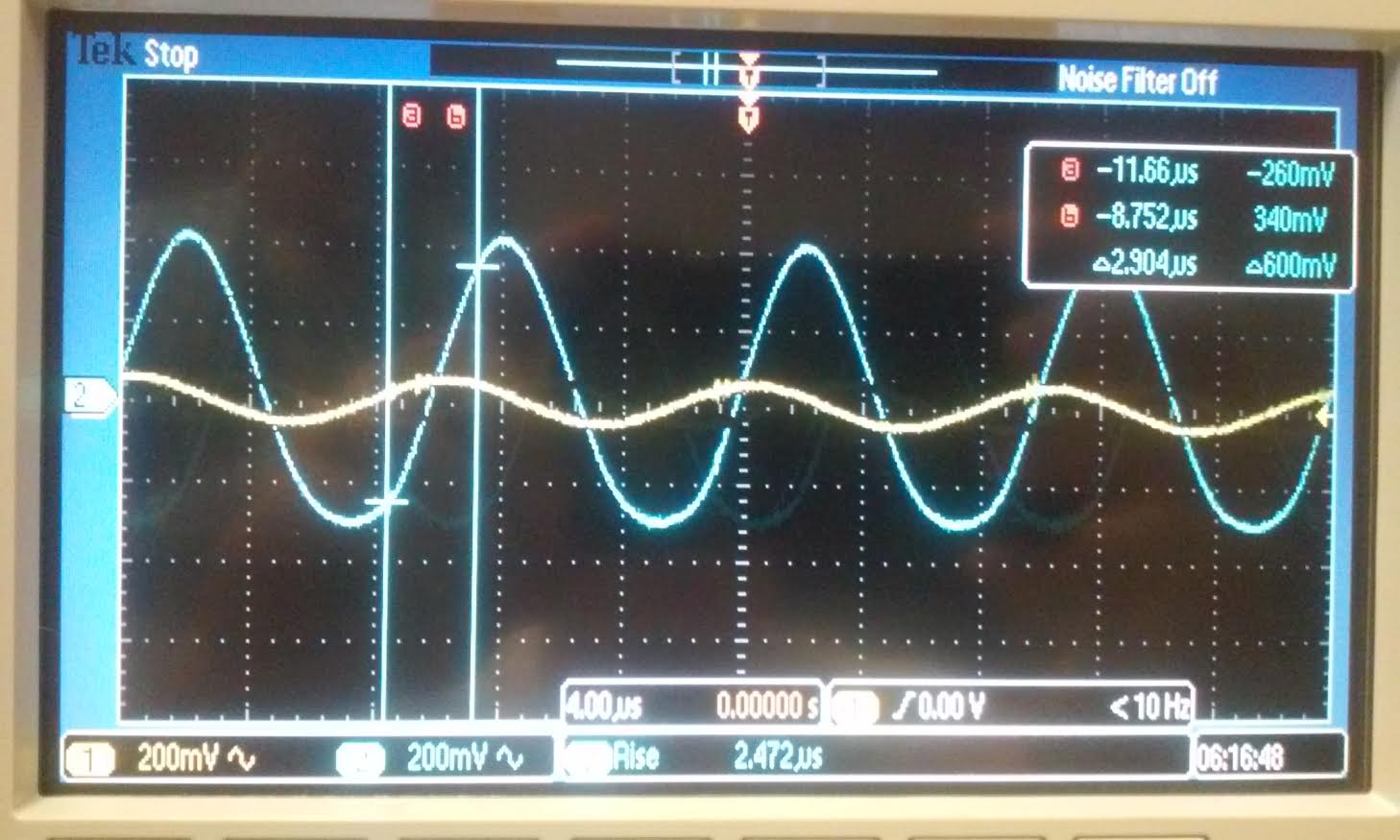Theortical	Pulse wave	Sine Wave
0.4 V/us	0.389 V/us	0.243 V/us

The slewrate is the rate of change of the output voltage with time (dV/dt), usually given as V/us. When we have an input of a square wave, the slew rate is more accurate than the input of a sine wave because for the square wave the output is able to keep up with the input. For a sine wave, the output change at the same rate as the input so the slewrate is unable to keep up. Therefore, for the sine wave input the slew rate is much slower than the theoretical value. This can be analyse using mathematic. SR = dV/dt. For a square wave; there is only one change, at the corner of the rising edge and the peek, the change in voltage is flat so it deriviative is faster to derive (it is a constant). But for a sine wave, dV/dt changes at everypoint, thus the slewrate is slower.

Conclusion: from this lab we can see that the unity frequency or GBP is equal to the gain times the Bandwidth, (GBP = Aol * BW) so for a given op-amp if we want a higher bandwidth then we need a lower gain, or vice versa. If we want to design with a higher gain and a higher bandwidth then we need an op-amp with a higher GBP. the difference between the non-inverting topology vs. the inverting topology is that with the non-inverting we get the higher bandwidth for a given op-amp. So if we want to maximize our bandwidth then we need to choose the non-inverting topology. However, this bandwidth difference between the two topology becomes less significant when we raise the gain. We can analyse the difference between the non-inverting vs the inverting by their BW equation: for non-inverting BW=Fun/Aol, for inverting BW = Fun/(1+Aol). so when Aol >> 1, then the two equation is the same.

Return to EE420L front page