EE 421L Digital Integrated Circuit Design - Lab 2

Design of a 10-bit digital-to-analog converter (DAC)

Shadden Abdalla

Abdals1@unlv.nevada.edu

PRELAB WORK

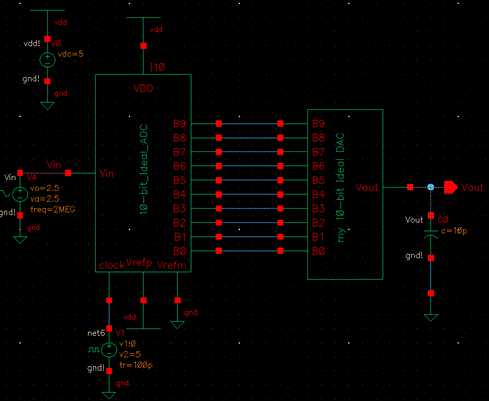
The relation between Vin B[9:0] and Vout:

The ADC captures a voltage at specific instances in time, the ADC reads Vin, and then converts Vin into a binary 10-bit number. Then the DAC reads the 10-bit number outputs the voltage at multiples of the LSB. Vout is a multiple of the LSB (4.88mV in this case). The output staircases at increments of 4.88mV, or at increments of the LSB.

Download lab2 file and extract it.

Define the file in cds.lib library

Open up the sim_Ideal_ADC_DAC schematic cell, launch ADE L, load state and output the Vin and Vout simulations of the schematic.

è è

Colors changed to show understanding of graph properties.

Below is the same circuit’s simulation except for with a different input voltage. I changed the amplitude and the offset to 5mV each.

------------------------------------------------------------------------------------------

REAL LAB WORK

This lab is the creation of a 10-bit DAC using n-well resistors following CMOS book topology from figure 30.14:

Calculating least significant bit (LSB) using this formula.

VDD= 5V, N=10.

LSB = 5V / 2^(10) = 5V / 1024 = 4.88mV

Schematic of 4.88mV = LSB shown on the top of the square wave

Schematic checked with no errors.

The design of a 10-bit DAC using an n-well R of 10k.

I created the schematic and checked and saved.

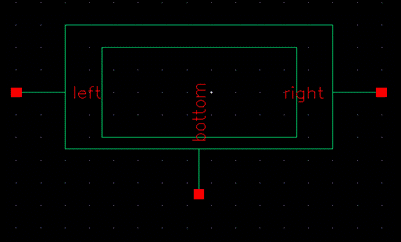
SYMBOL 1:

Below is the symbol compared to the ideal one already given to me. I used the same size as the one already made.

Above is my finished symbol of the resistor part of the DAC. I am going to connect ten of them together to create the 10-bit DAC.

Below is the 10-bit DAC using the DAC symbol that I made. I connected them all together from B9-B0 and then connected the bottom of B0 to a 10k resistor and ground.

Regular size above. Above is the zoomed in version broken into two parts.

SYMBOL 2:

Below is the symbol I made for the 10 bit DAC that I made above, compared to the one that was given to me in lab two (the ideal one).

ç my new symbol

I moved the shape from the ideal one and copied it into my 10 bit DAC (and the pins from my schematic) and then renamed the symbol and deleted the ideal DAC symbol remains that I didn’t need.

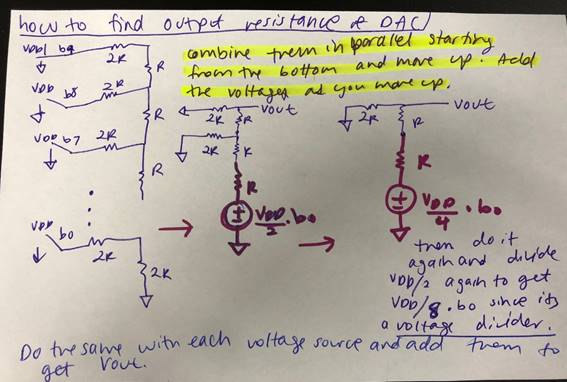
HOW TO DETERMINE THE OUTPUT RESISTANCE OF THE DAC, R, BY COMBINING RESISTORS IN PARALLEL AND SERIES.

The circuit is a voltage divider that moves upwards. A voltage divider with two equal values of resistance has a Vout = (Vin/2)*bx thus the output after moving up once and combining the resistances using a voltage divider is VDD/2*bx. The x denotes any value of b that moves upward, depending how many bits are in the circuit. Since the DAC has ten bits, it will move upwards from b0 to b9. Every time you move up, you will continue to divide the voltage by two while making sure to multiply by the value bx of that specific isntance. If the circuit started at b0 and ended at b2, you would use three voltage dividers and divide the VDD 3 times. The first time the input will equal b2*(VDD/2), the second time will result in b1*(VDD/4). The third time the answer will also divide again by two and equal b0*(VDD/8).

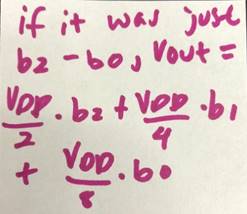
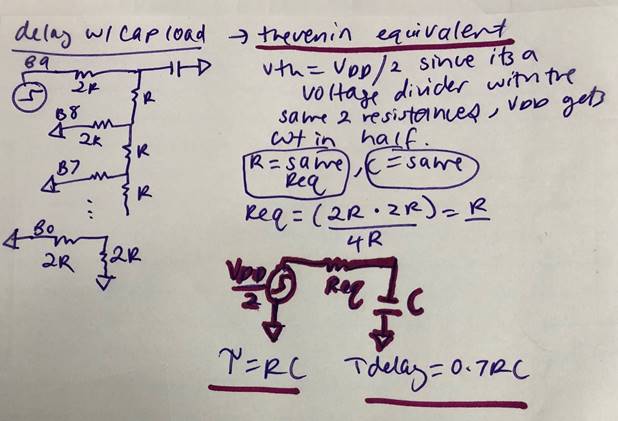
DELAY, DRIVING A LOAD. Ground all DAC inputs except B9. Connect B9 to a pulse source (0 to VDD) and show, and predict using 0.7RC, the delay the DAC has driving a 10pF load.

Calculating the time delay: è = 69.9 nanoseconds

A delay of 69.9n is shown above in the capacitor with the simulation shown to its right

CAPACITIVE LOAD

Adding a 10pF capacitive load changes the phase of the output in comparison to the input voltage. The output lags the input by about 69 nanoseconds which mirrors the time delay that we inputted earlier onto the capacitor. The input reaches peak at about 629.48ns and the output reaches peak at about 699.317ns, showing that they are out of phase by about 70nanoseconds which is consistent with the above capacitor delay. It is interesting, because even without adding the delay, the circuit lagged the input the same amount.

NO LOAD

Now I’m going to copy my design into the original schematic, renamed sim2 so that I know the difference and will test to see if my schematic works just as well as the original.

Below is the result with my DAC Below is the original circuit from the ideal DAC

The results are the same and as expected, showing that the DAC I made works under no load.

RESISTOR

Adding a 10 kohm resistive load below. Adding the resistor cuts the output voltage in half at the peak but the trough of the graph stayed the same. They are also in phase and created a voltage divider at the output.

RESISTOR AND CAPACITOR

Adding both components from the above circuit, a resistor and capacitor load, changes the output much more drastically than adding one or the other. The input reaches peak at about 629.481us where the output reaches peak at about 676.076us which shows a delay between the input and output of about 47microseconds.

• In a real circuit the switches seen above (the outputs of the ADC) are implemented with transistors (MOSFETs). 
• Discuss what happens if the resistance of the switches isn't small compared to R.

If the resistance is not small compared to R, the overall resistance will increase which will reduce the size of the output voltage that the circuit will produce since more of the voltage will dissipate within the resistance. Less resistance will allow more voltage to output whereas more resistance will cause some of the voltage to dissipate before it can output.

I then backed up my work, zipped it up and put it in my google drive.

Return to Dr. Baker's Students