Project - ECE 421L
See the EE421L webpage here

Authored by Juan Buendia
buendiaj@unlv.nevada.edu
November 8, 2015

Objective: To learn how to implement various logic gates to create an eight-bit resettable (input"clear") up/down counter

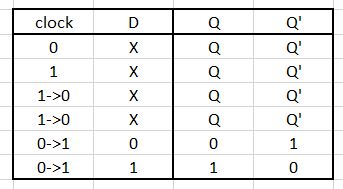
One of the ways to implement a resettable (input "clear") up/down counter is by using edge-triggerted D flip-flops with a clear, and it will also make the countter edge triggered.   Implementing edge triggered clocks allows the user to change its input without affecting the output untill there is either a rising edge or a falling edge of the clock.  A D flip-flop is a flip flop that simply passes the it's input (D) to the output Q with Q' as the logical opposite of Q, and the clear will set all outputs to 0 (clear out any latched outputs).  My design will use D flip-flops which have an active high clear and are positive edge-triggered.

Truth Table



Schematic



This implementation of a D flip flop uses two cascaded clocked latches.  In their simplest form, a clocked latch is simply two pass gates (the NMOS and PMOS devices) and two inverters.  The left most pass gate has the clock to the PMOS device with the inverted clock to the NMOS Device, and the opposite is true with the second pass gate.  This makes the first latch allow the input to pass when the clock is high.

The second latch has the clock inputs inverterd to its respective passgates, and the inverter and NAND are also switched.  This makes the D flip flop positive edge triggered.  

Notice the clock (Clk) has two inverters.  Since I will clock each flip flop in parallel, this will help to buffer each flip flop's clock.

The Nand Gates serve serve to set the output to 0 when the "Clr" signal is 1.  This will place a logic 0 on one of the inputs to the NAND Gates which will lock their output to 1.



Symbol



Simulation Schematic



                                  Layout                                                                                                Extracted



DRC



LVS



Schematic Simulation Results



Extracted Simulation Results



In the counter, a total of eight D flip-flops are needed to obtain the eight bit ouput.   I will trigger all eight flip-flops at the same time, however if I was to simply tie each Q output to the next D input, it will simply will not count.  In order to fix this issue,  I will use a truth table to find out what the next state is for each of my current states (ex. if current state is 00000000, then the next state is 00000001 for counting up and 11111111 for counting down).

Truth Table (for the first four bits)



Looking at each individual bit, we can derive a boolean expressionn for each of them.

Counting up
C0+ = C0'
C1+ = C0C1' + C0'C1 (XOR Gate)
C2+ = C2'C1C2 + C2(C1C2)'
C3+ = C3'C2C1C0 + C3(C2C1C0)'
C5+ through C7 follow what C2 and C3 were doing (Cn+=Cn'Cn-1Cn-2...C0 + Cn(Cn-1Cn-2...C0)')

Counting down
C0+ = C0'
C1+ = C0C1 + C0C1 (XNOR/Equivalence Gate)
C2+ = C2(C1+C2) + C2'(C1+C2)'
C3+ = C3(C2+C1+C0) + C3'(C2+C1+C0)'
C5+ through C7 follow what C2 and C3 were doing (Cn+=CnCn-1Cn-2...C0 + Cn'(Cn-1Cn-2...C0)')

If we look carefully at C1 while counting up:
When C2 = 0 then C2+ = C1C2 (AND Gate), and when C2=1 then C2+ = (C1C2)' (NAND Gate)).
This can be implemented using a multiplexer.  

A multiplexer is a device that takes several inputs and chooses which input to place on its output.  In this 8 bit counter I used a series of 2:1 MUX/DEMUX.
When its input S is 0, then it places the its input A on the output, and when its input S is 1, it places its input B on the output.

I decided to buffer the selector input S using two inverters.  The first inverter buffers and inverts the S and the second inverter buffers and changes the signal back to the original S bit.  This was done because there will be several 

As stated before, the MUX/DEMUX I used  was implemented using two pass gates.  When they are active, it will pass their input to the output, but they become high impedance when not selected.

Pass Gate Schematic

Schematic




The 10 megaohm resistor is to demostrate when the gate is passing the input and when it is not.  

                           Layout                                                         Extracted



DRC



LVS



Simulation Regular Results




Simulation Extracted Results




Using eight total D flip flps I derived the eight bit output signal for the counter.  I had to use the truth table and implement multiplexers, NAND gates and inverters  to make it work.

8-bit Up/Down Counter With Asynchronous Clear



First two bits



Note how the multiplexer is placed as the up/down selector, and each A,B,C...H net is connected to C0, C1...C7 respectively.

When S is zero, the multiplexer's B input is selected, and the circuit will count up.  When S is 1 the multiplexer's A input is selected and the circuit will count down by placing the output of an XOR GATE when counting up and the inverted XOR Gate output (XNOR) when counting down.



The third bit allows the NAND and AND's the first two inputs to produce the C2+ output when counting up.  When counting down, two multiplexers are used to switch from C0 and C1 to C0' and C1' (they are taken from the Q' outputs of the first two D flip flops.  This is done  since inverting the inputs to a NAND gate produces the same output of an OR gate.  

Demorgans theorem
(AB)' = A' + B' so inverting the inputs produces A + B.


4th through 8th bit


Symbol



The fourth throgh the eigth bit follow the same format that the third bit does except only one input is switched.  The other input was switched with the previous D flip flop

Layout





Extracted



DRC



LVS



Simulation Schematic



Simulation resutls counting up



Simulation resutls counting down



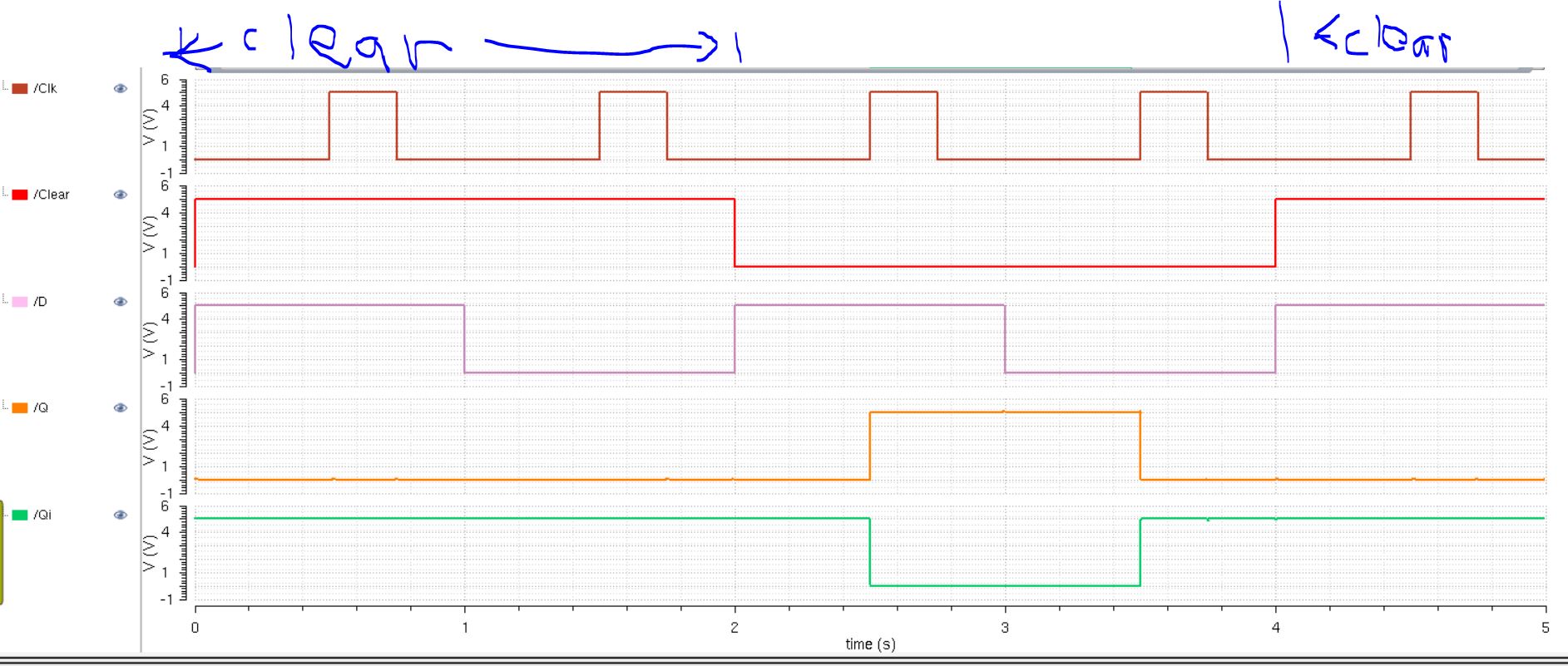
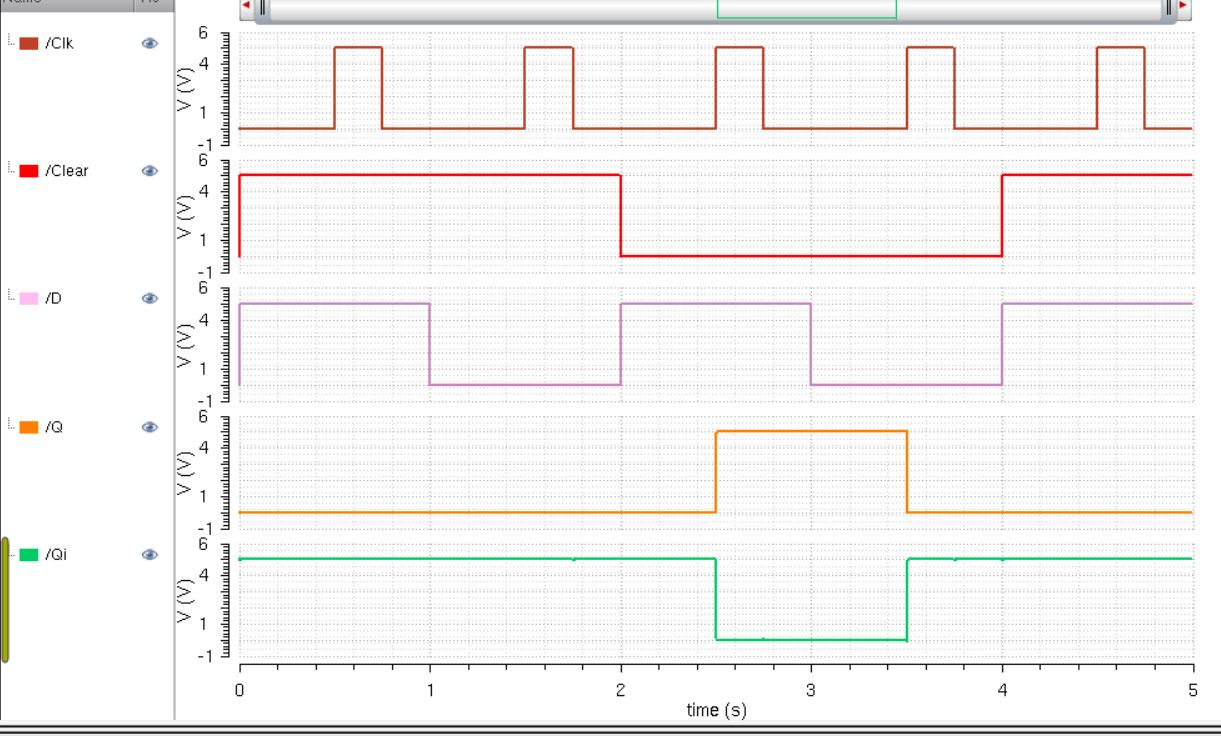
Counting down then clear



Counting up then clear



Extracted UP



Extracted Down


zip