Lab

Lab 4 Op-amps II, gain-bandwidth product and slewing- EE 420L

Authored by Jeremy Garrod

2/22/2017

garrod@unlv.nevada.edu

Pre-Lab Work

Watch the video op_amps_II, review op_amps_II.pdf (associated notes), and simulate the circuits in op_amps_II.zip.

Read the write-up seen below before coming to lab.

Lab Work

Estimate, using the datasheet, the bandwidths for non-inverting op-amp topologies having gains of 1, 5, and 10.

The gain-bandwidth product can be used to estimate the bandwidths for each of the listed gains. The unity gain frequency is the frequency when the gain is 1 or 0dB, given this information, the gain-bandwidth product can be determined and then used to calculate the bandwidths of any gain.

The datasheet states that the gain-bandwidth product is 1.3MHz. Therefore the following calculations represent the expected bandwidths of each gain.

Hand calculations for bandwidths of non-inverting topology

Experimentally verify these estimates assuming a common-mode voltage of 2.5 V.

Your report should provide schematics of the topologies you are using for experimental verification along with scope pictures/results.
Associated comments should include reasons for any differences between your estimates and experimental results.

In order to verify these estimates, two different measurements must be made for each gain. The first measurement is at a low frequency in order to get a baseline value for the output of the circuit. The next measurement is at the -3dB point or .707 of the initial output value, which will tell us the resulting bandwidth for each gain. The low frequency that was used was 1kHz, due to the fact that I was almost half way done before I realized I did not change the frequency that the function generator was already set to, so I just kept going with it. At the end of this experiment, there will be a table that summerizes the values pictured below.

For a gain of 1:

Schematic for non-inverting Op-amp with a gain of 1

Ideally, there would be no resistor between VCM and the inverting terminal of the Op-amp. However, there was an issue with the signal having some weird noise at the bottom of the sine wave, so a 100k resistor was added to the circuit which seemed to clean it up. I can't think of an explanation as to why, it was just something that was discovered out of trial and error. The only consequence I was able to find was that my VCM measured slightly lower than the desired 2.5V.

I could not find the image of the waveforms at 1kHz. However, the ouput voltage was fluctuating quite a bit between about 90 and 130mV so I took the average and assumed that the output was 110mV for the sake of simplicity. The image for the inverting Op-amp with a gain of 1 had the same exact output, just in phase with the input, which can be seen below.

One more note, the oscilloscope I was using did not display the correct -3dB frequency the majority of the time. For that reason, there will be an image of the function generator for each incorrect frequency.

Waveform of the non-inverting Op-amp with a gain of 1 at 1.25MHz

For a gain of 5:

Schematic for non-inverting Op-amp with a gain of 5

Waveform of the non-inverting Op-amp with a gain of 5 at 1kHz

Waveform of the non-inverting Op-amp with a gain of 5 at 130kHz

For a gain of 10:

Schematic for non-inverting Op-amp with a gain of 10

Waveform of the non-inverting Op-amp with a gain of 10 at 1kHz

Waveform of the non-inverting Op-amp with a gain of 10 at 45kHz

Gain	Vout	Measured Vout*.707	Ideal Bandwidth	Measured Bandwidth
1	110mV	76mV	1.3MHz	1.25MHz
5	456mV	312mV	260kHz	130kHz
10	960mV	680mV	130kHz	45kHz

The measured bandwidth was very similar to the ideal bandwidth at lower gains. The higher the gain became, the farther apart the measured bandwidth was from the ideal that was calculated. This could be due to many factors including process differences as well as human error in the measurements. Another possibility is the fact that a different VCC and peak voltage were used in this experiment than were used in the datasheet. Lastly, my VCM was a little off, so that could have been a contributing factor as well.

Repeat these steps using the inverting op-amp topology having gains of -1, -5, and -10.

Hand calculations for inverting topology

For a gain of -1:

Similar to the non-inverting topology, the output voltage for a gain of -1 at 1kHz varied between about 90 and 130 so a value of 110mV was used.

Schematic for inverting Op-amp with a gain of -1

Waveform of the inverting Op-amp with a gain of -1 at 1kHz

Waveform of the inverting Op-amp with a gain of -1 at 575kHz

For a gain of -5:

Schematic for inverting Op-amp with a gain of -5

Waveform of the inverting Op-amp with a gain of -5 at 1kHz

Waveform of the inverting Op-amp with a gain of -5 at 95kHz

For a gain of -10:

Schematic for inverting Op-amp with a gain of -10

Waveform of the inverting Op-amp with a gain of -10 at 1kHz

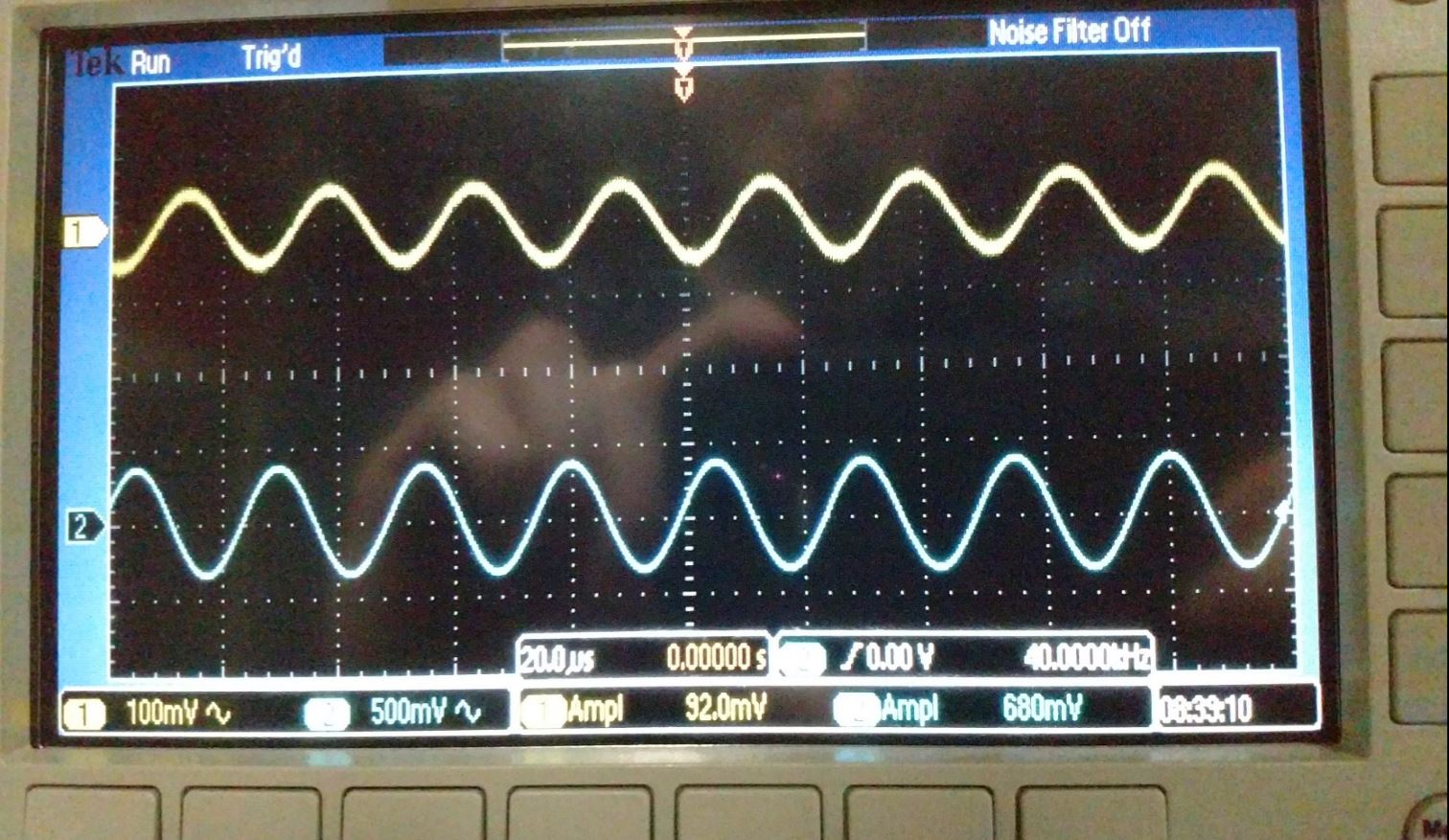
Waveform of the inverting Op-amp with a gain of -10 at 40kHz

Gain	Vout	Measured Vout*.707	Ideal Bandwidth	Measured Bandwidth
-1	110mV	72mV	650kHz	575kHz
-5	488mV	328mV	217kHz	95kHz
-10	960mV	680mV	118kHz	40kHz

Design two circuits for measuring the slew-rate of the LM324. One circuit should use a pulse input while the other should use a sinewave input.

Provide comments to support your design decisions.
Comment on any differences between your measurements and the datasheet’s specifications.

For this design, I used the non-inverting topology from the beginning of the lab. This allows for the rise of the ouput to be directly compared to the input since they should be close in phase as well as the close to the same amplitude. The slew rate is the change in voltage over the change in time. In order to measure this, a signal at 300kHz and a p-p of 500mV was put through the Op-amp. The time from 10% to 90% of the signal strength was then measured. This allows the output to get as linear as possible before looking at the values.

Schematic of circuit used to calculate slew rate

Change in voltage and time for square wave input

Change in voltage and time for sine wave input

Slew rate hand calculations

LM324 datasheet slew rate

The slew rate that was measured was a little bit lower than the slew rate listed on the datasheet. This could easily caused by the fact that I used a different VCC along with non-ideal VCM, process differences, etc. I also did not use a load to test my circuit, where as they did in the datasheet. Other than those things, I am not sure why my values would be as different as they are.

Return to EE 420 Labs