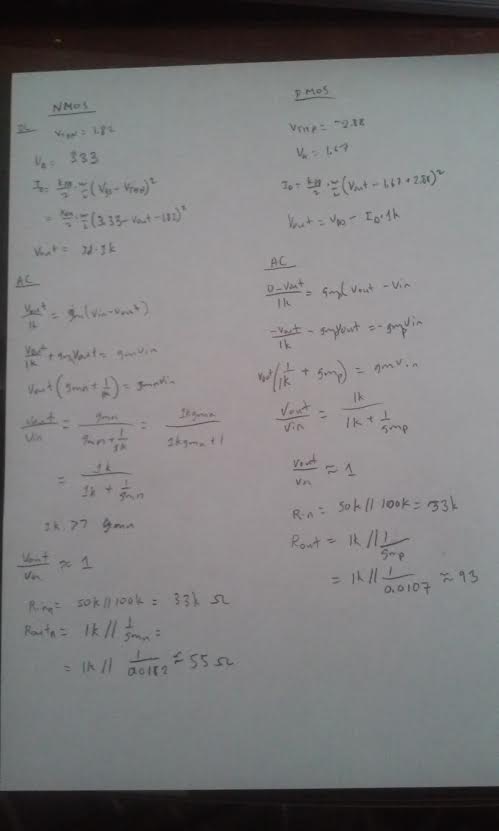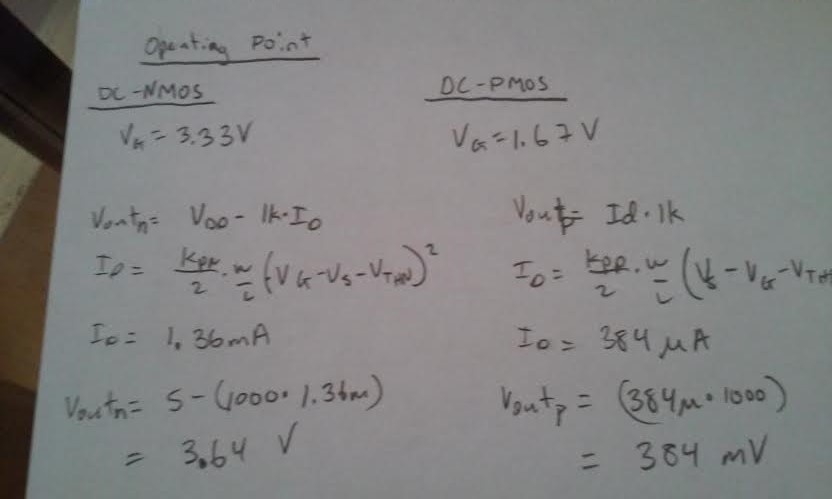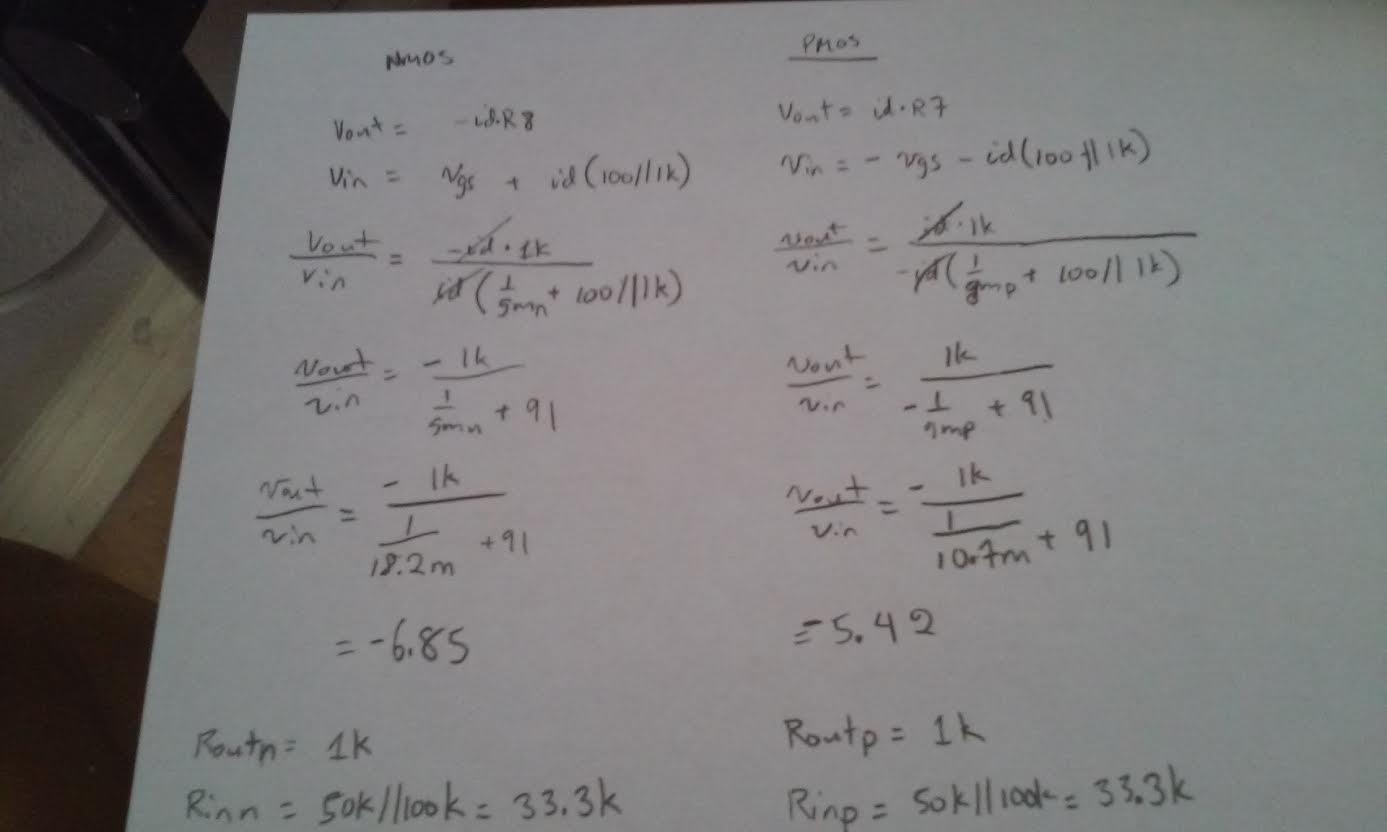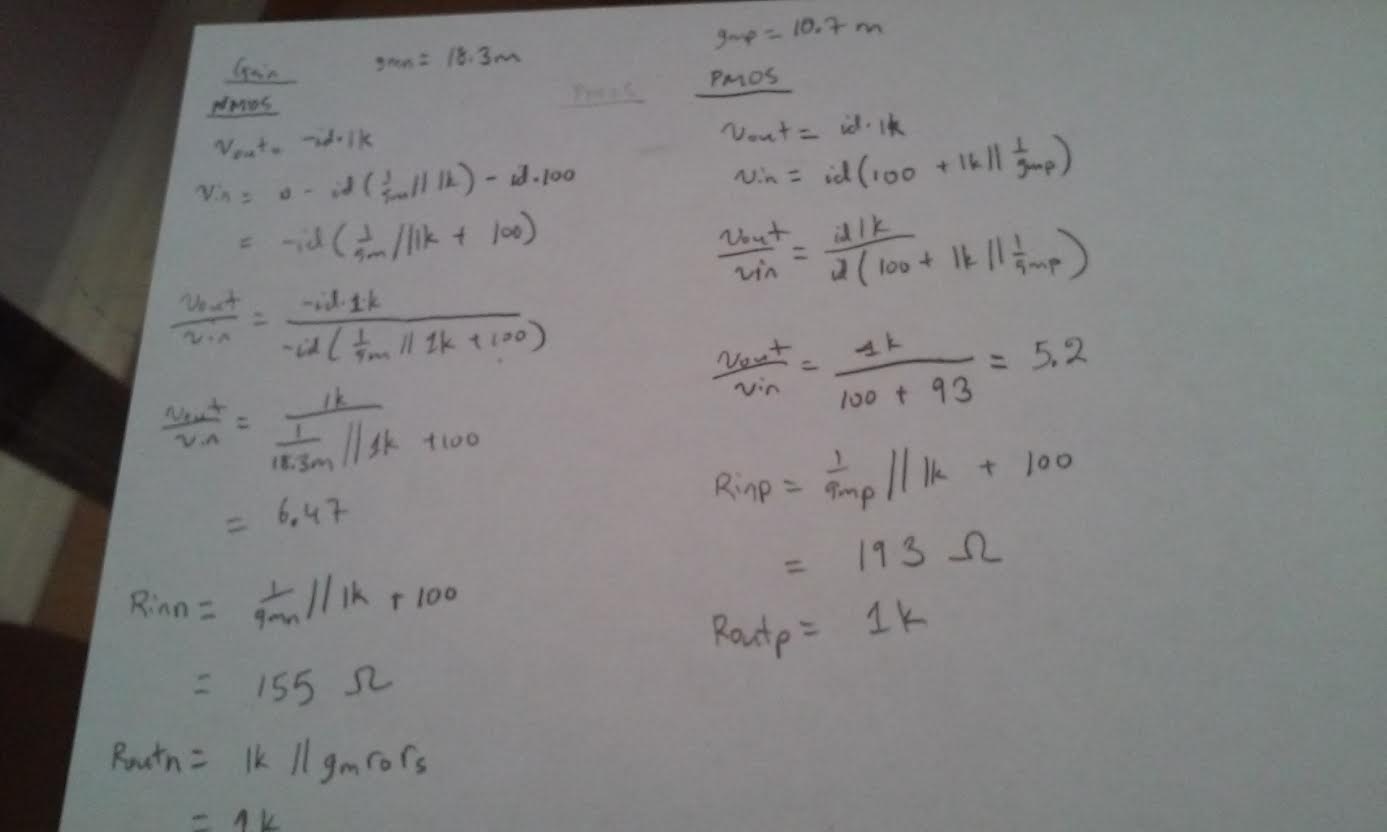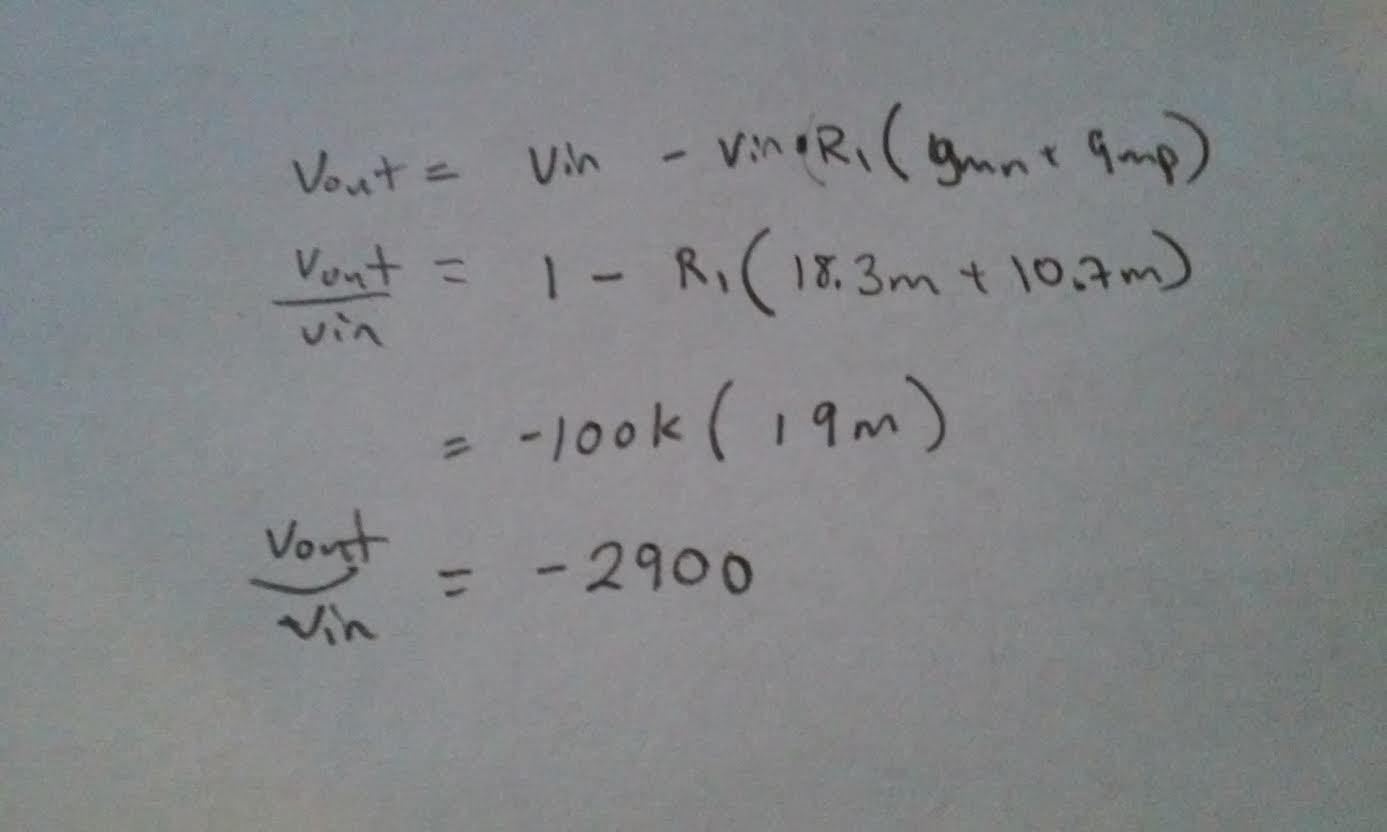Lab

EE 420L Engineering Electronics II Lab - Lab 6

Nha Tran
03/15/2015

NSHE: 2000590233

trann4@unlv.nevada.edu

Single-Stage Transistor Amplifiers

Below are schematics for NMOS and PMOS source followers amplifiers (also known as common-drain amplifiers).
In your lab report discuss the operation of these circuits.

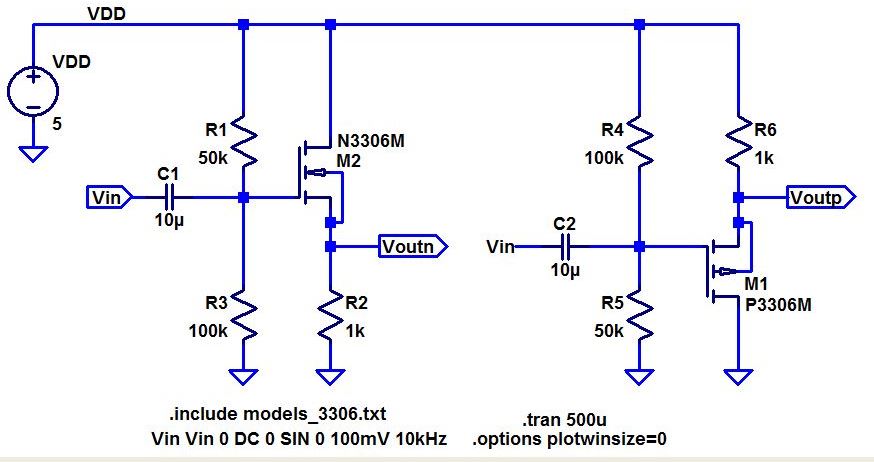
Simulate the operation of these amplifiers.

Hand calculate, and then verify your hand calculations with experimentation and simulations, the gains and the input and output resistances ensuring that your test signals are at a high enough frequency that the caps have negligible impedance but not so high that the gain is dropping off.

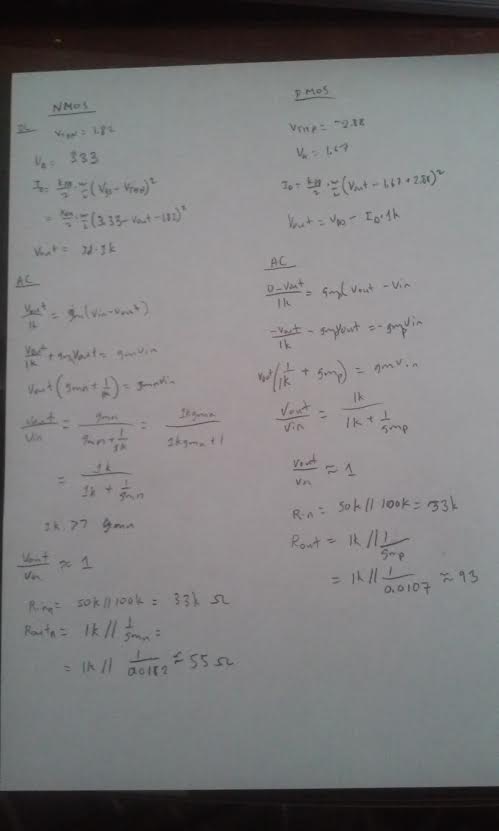
If you build this circuit using electrolitic capacitors, assuming the input AC signal swings around ground, put the "+" terminal of the cap on the gate of the MOSFET. Please indicate, in your lab report, that you understand why the capacitor is connected this way.

We used electrolitic capacitor in our circuit and we connect the terminal with the higher potential is positive and the lower potential is negative.

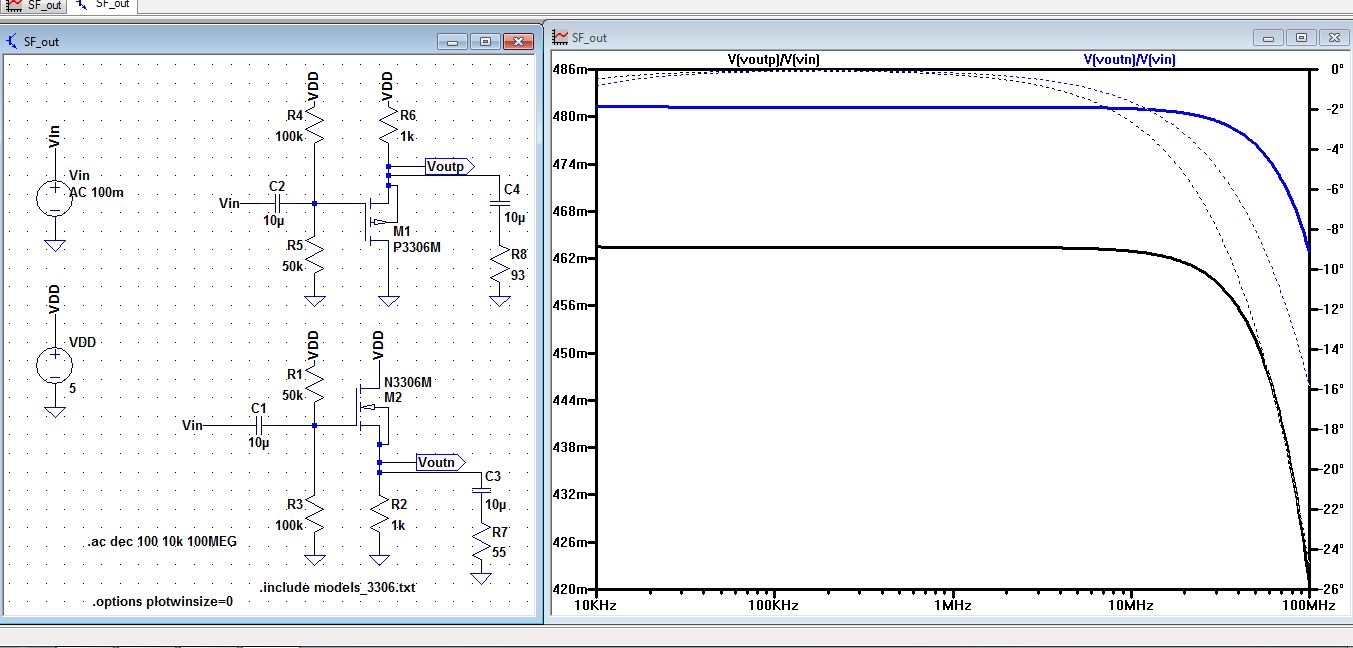
Simulations for the gain of the source follower amplifier.

The transient analysis along with the circuit was drafted by Dr. Baker it shows that the gain for the Nmos = Pmos =1.

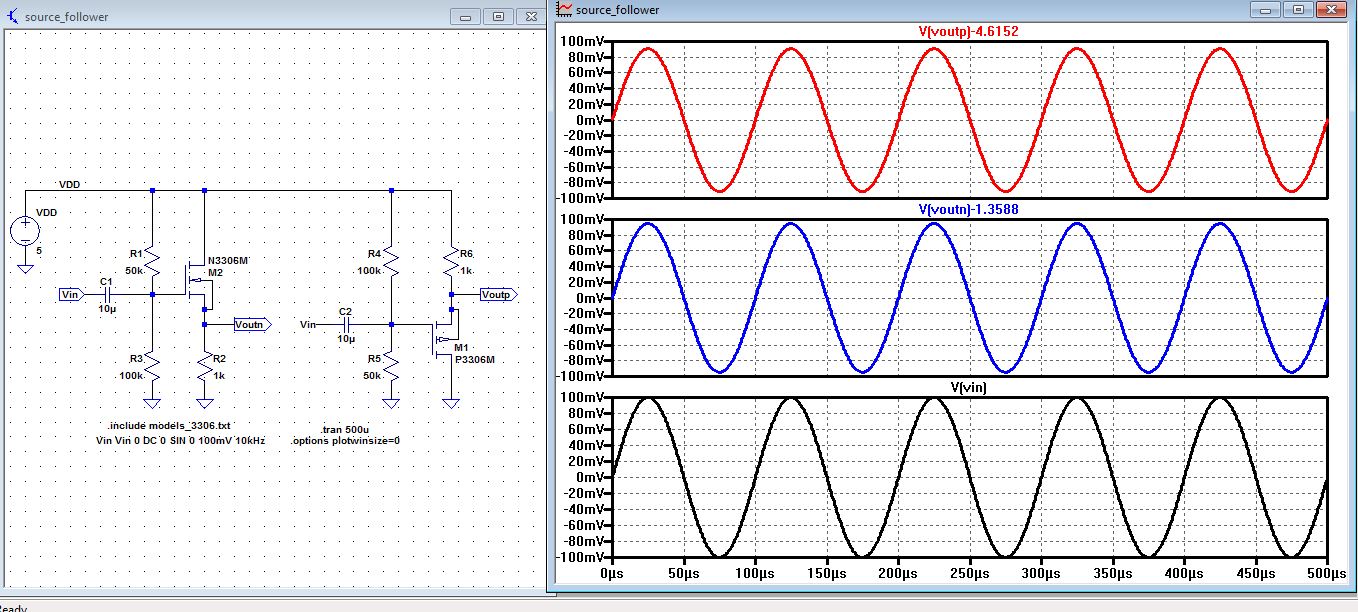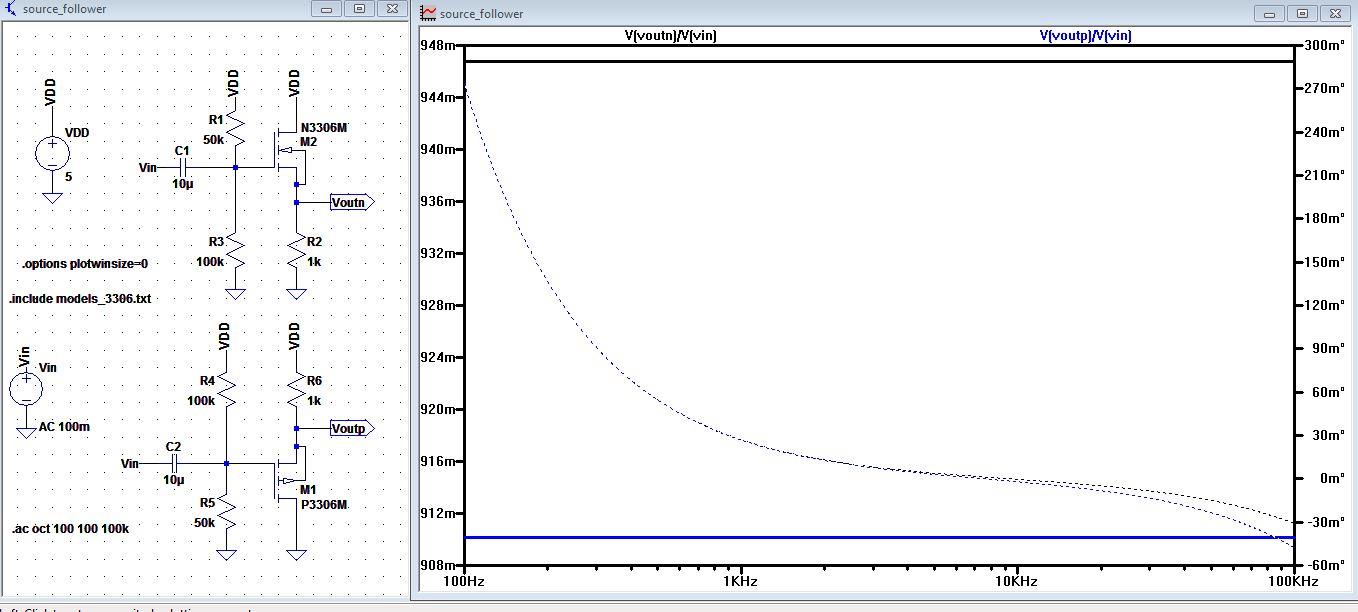
Doing the AC analysis and taking the reading at 10 kHz. The gain for Voutn/Vin = 0.946. And the gain for Voutp/Vin = 0.910. Both roughly equals 1.

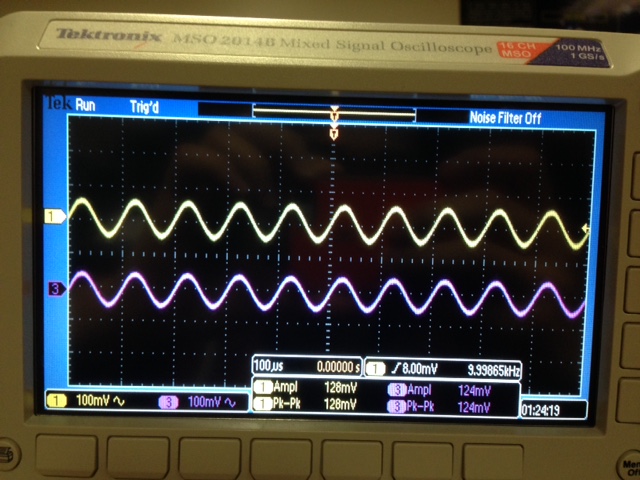
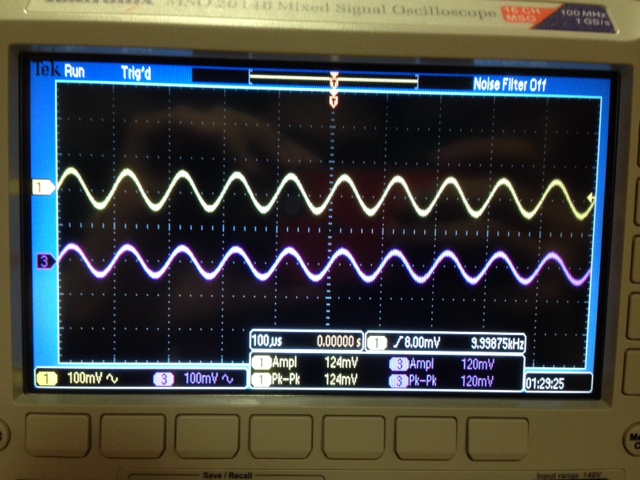
Experimental scope reading of the gain for Voutp and Voutn
Voutn: as you can see the the reading below the output matches the input so the gain is 1, which is the same as our simulation and hand calculation	Voutp: vout is approximately Vin so vout/vin=1

In your lab report discuss, in your own words, how to measure the input resistance.

For measuring the input resistance add a resistor equal to the value you calculated between the input voltage source and the amplifier.
Measure the peak AC current through this added resistor by taking the difference in the peak AC voltages across the resistor (on one side is the input voltage signal and the other side is the connection to the amplifier's input capacitor) and then dividing by the resistor's value.
Measure the peak AC voltage on the input of the amplifier (the left side of the capacitor).
Dividing this peak AC voltage by the peak AC current through the added resistor is the amplifier's input resistance.

To measure the input resistance we see that the resistance before Vin is 100k|| 50k, both are connected to AC ground so the input resistance is 33k. to measure the input resistance of the circuit we have to put 33k resistance right after our input, but before the 100l|| 50k that way the input amplitude gets divide in half before the signals goes into the amplifier. the result of this is that our output should be half of what it would have been if we did not added the 33k resistor. in our case we should see the output is ~.5V, since we original output was ~1V.

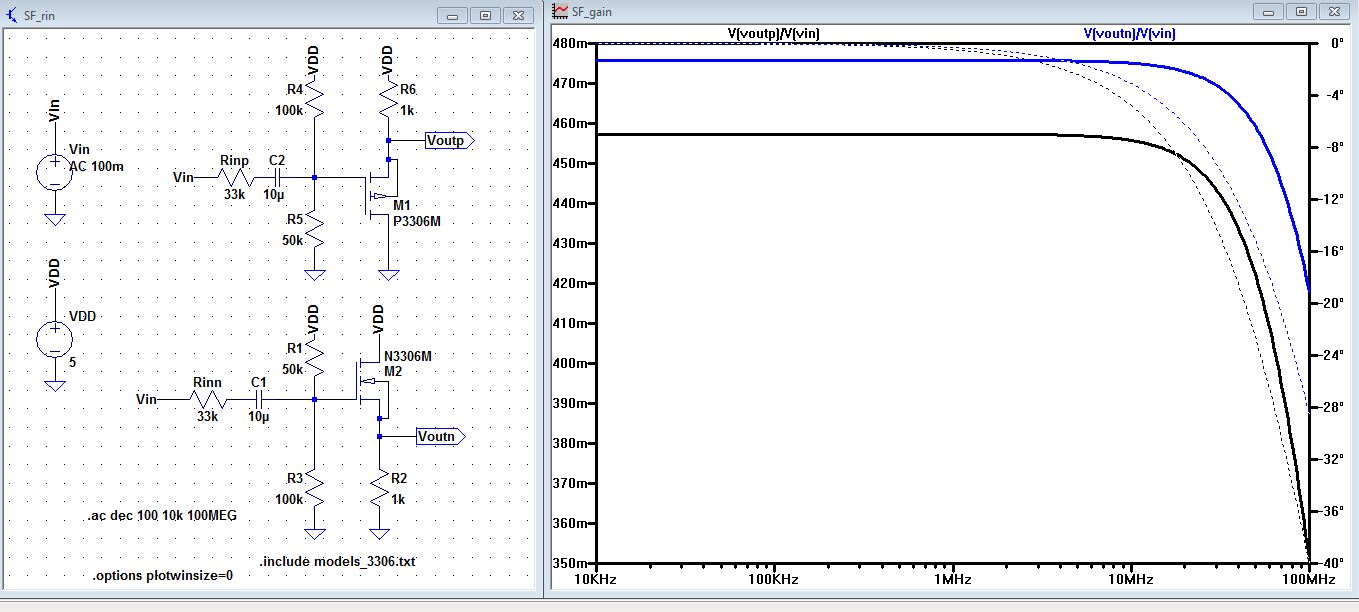
Simulation and experiment of Rin
As you can see below the Voutp/Vin and Voutn/Vin is now roughly half of what it was before when a 33k resistor is placed before the capacitor.

Nmos: in the experiment we placed a 33k resistor at the same position as the schematic and we got Voutn/Vin is roughtly half	Pmos: same as the Nmos side

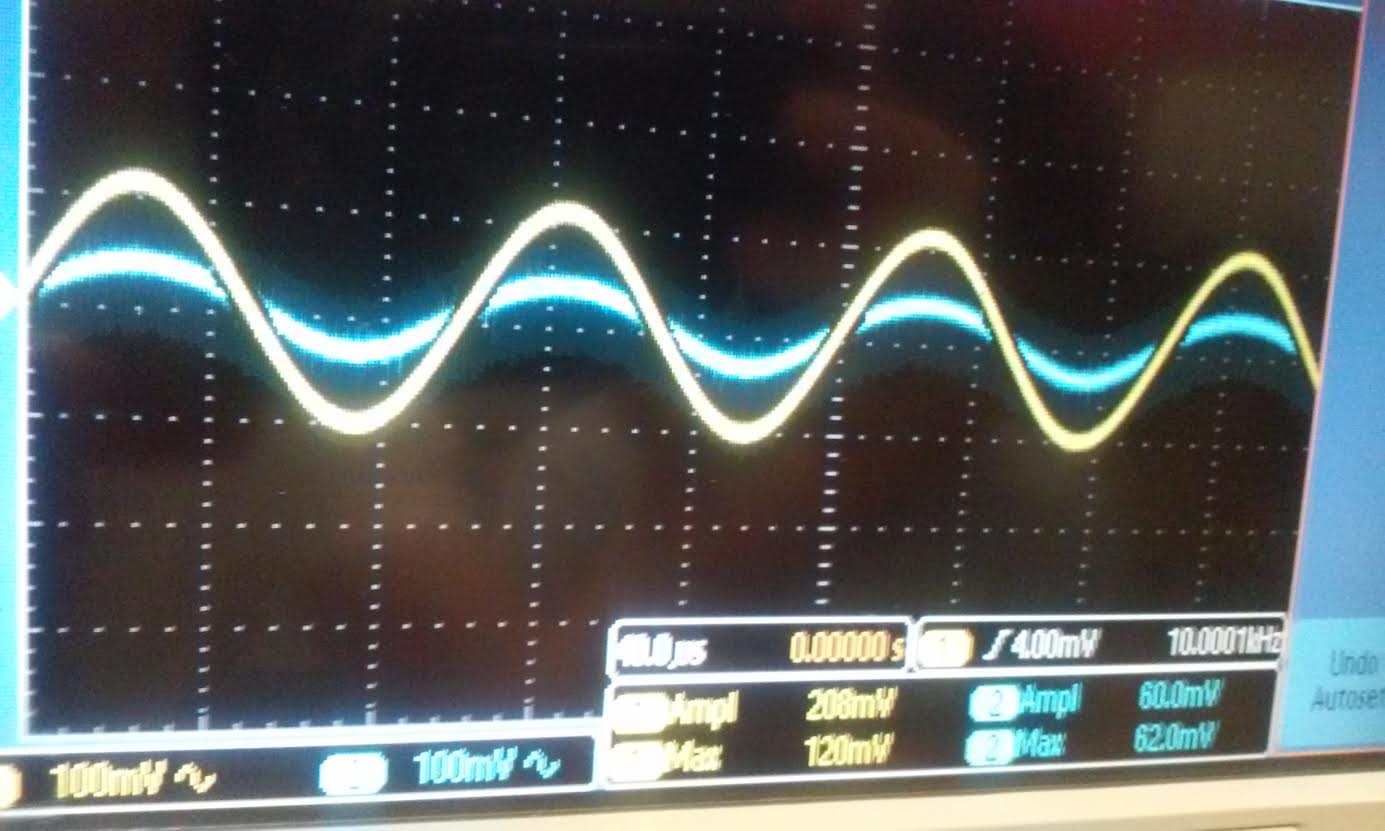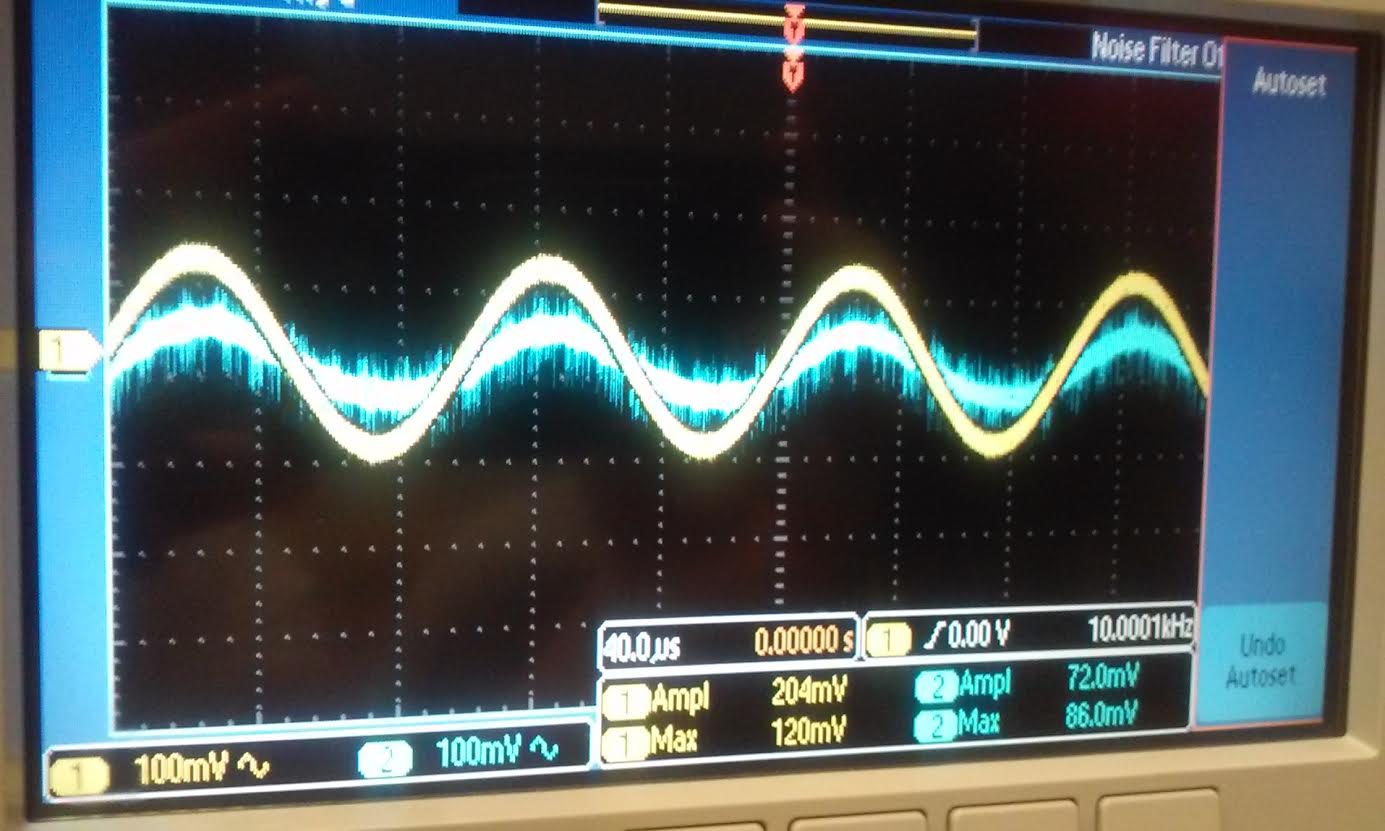Again, in your lab report discuss how to measure the output resistance.

For measuring the output resistance, add a resistor equal to the value you calculated in series with a big capacitor (to avoid messing up the biasing) from the amplifiers output to ground.
Measure the peak AC current through this added resistor.
Measure the peak AC voltage (remove the DC component) on the gate of MOSFET and the peak AC voltage on the source of the MOSFET. The difference in these two AC voltages is the peak AC gate-source voltage of the MOSFET.
Dividing this peak AC gate-source voltage by the peak AC current through the added resistor is the amplifier's output resistance.

To measure the output current we use the calculated values and add them in series with a 10u capacitor, and we connected in parallel to the 1k resistor for the Nmos and for Pmos we add it parallel to the Pmos device. From the hand calculation we got 55 Ohms and 93 Ohms for the Nmos and Pmos respectively. You can see from the schematic below how to hook up the calculated Rout to get the desired results.

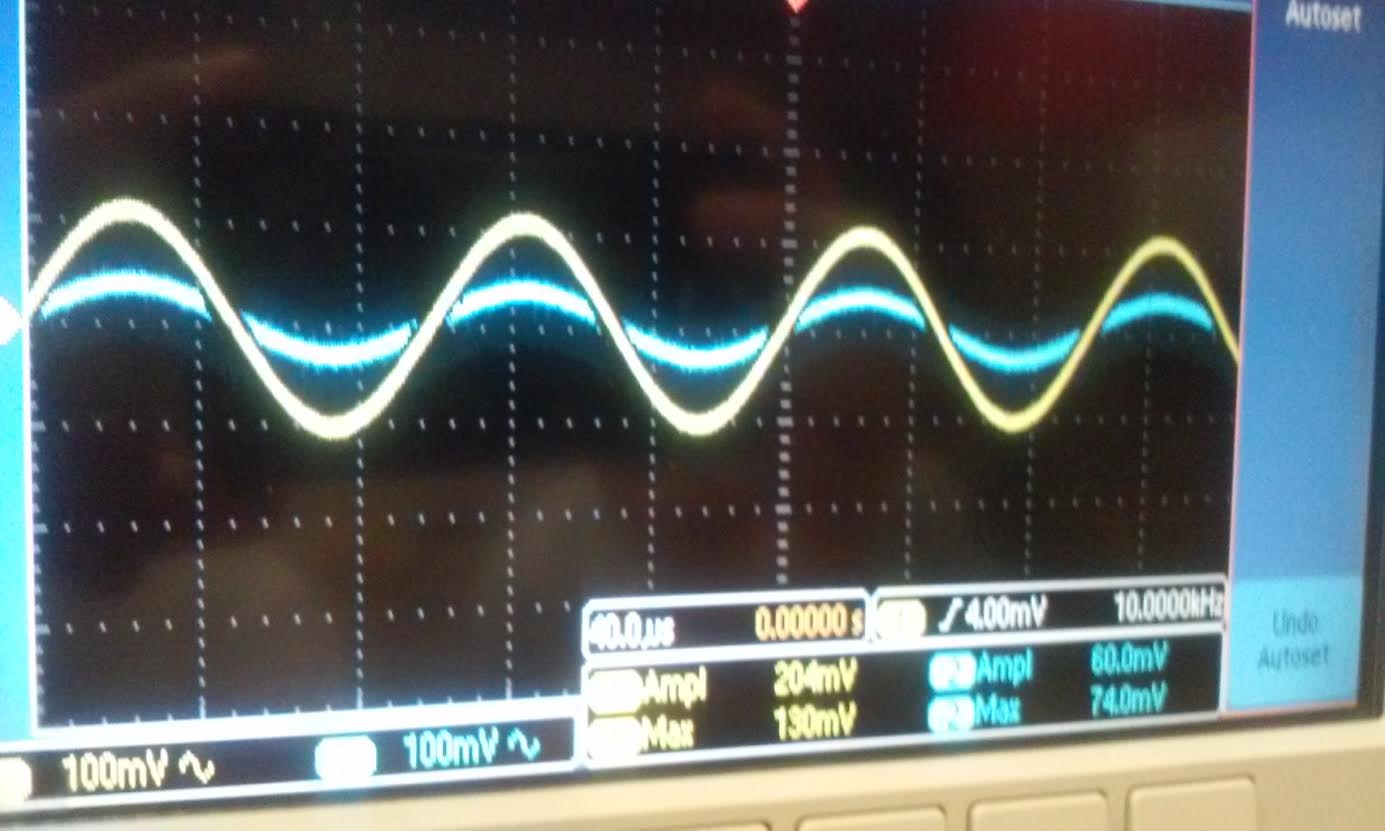
Simulation and experiment of Rout
As you can see when we hooked up 55 Ohms and 93 Ohms to the output of Voutn and Voutp our gain Voutn/Vin and Voutp/Vin is roughly half of 1.

Nmos	Pmos

Summary: Nmos
	Hand Calcution	Simulation	Experimental
Gain	1	0.946	0.968
Rin	33k Ohms	33k Ohms	33k Ohms
Rout	55 Ohms	55 Ohms	62 Ohms

Summary: Pmos
	Hand Calculation	Simulation	Experimental
Gain	1	0.910	0.969
Rin	33k	33k	33k
Rout	93 Ohms	93 Ohms	390 Ohms

Below are two common-source amplifiers.

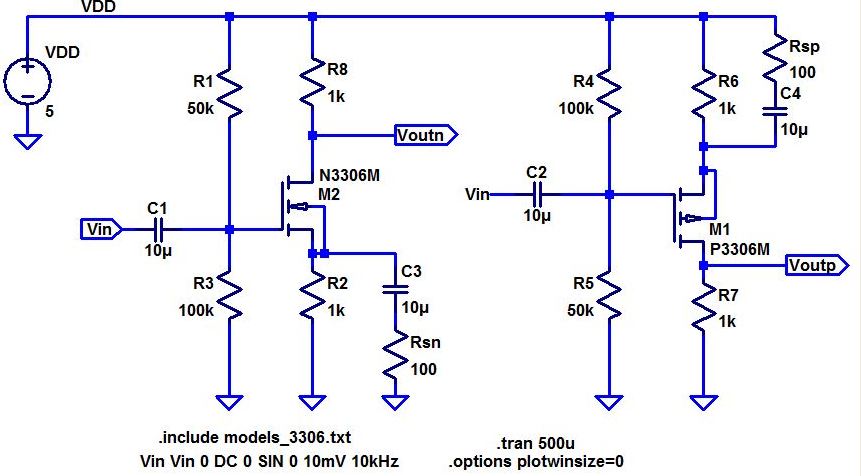
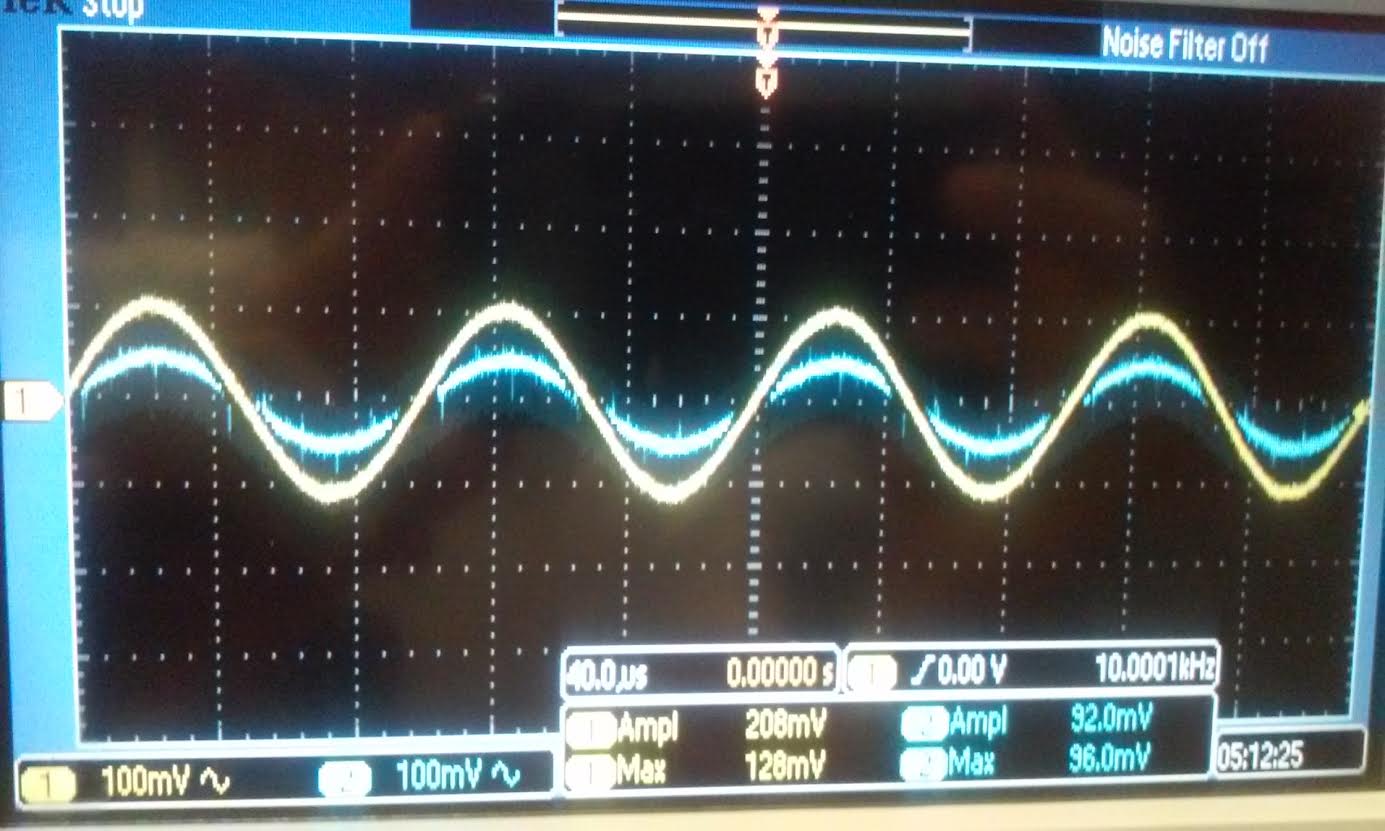
Discuss the operation of these amplifiers in your lab report including both DC and AC operation.

The DC operating point for the NMOS from looking at the spice error log and the hand calculation below you can see that gm=18.3mA/V, and Vout =VDD-id*1k = 3.64V. for the PMOS side the gm is 10.7mA/V and Vout =id*1k = 384mV, the threshold voltage is also taken from the spice error log its value is 1.82V for Nmos and -2.88V for Pmos. For AC vdd = 0V, so the operating point Rout and Rin is limited by the 1k resistor and 50k||100k. Vin and Vout will be limited by the hand calculations of the gain for AC below.

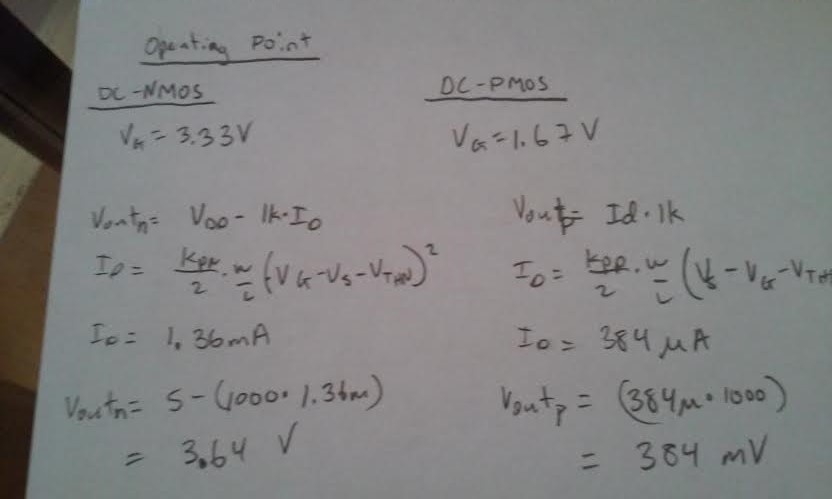
Hand calculate the gains and the input/output resistances.

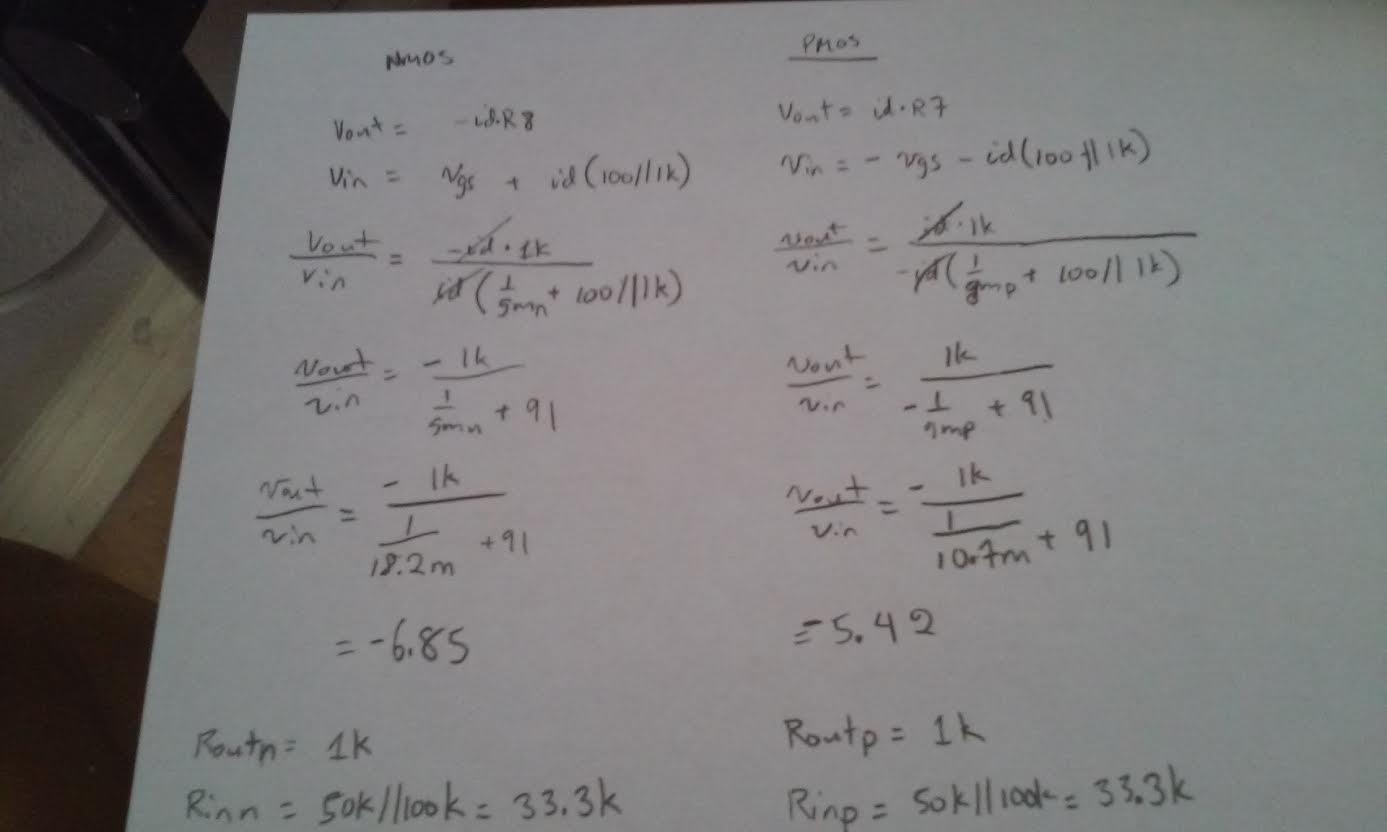
How does the source resistance, Rsn or Rsp, influence the gain.

If we increase Rsn or Rsp then the gain will decrease.

Again compare your hand calculations to simulation and experimental results.

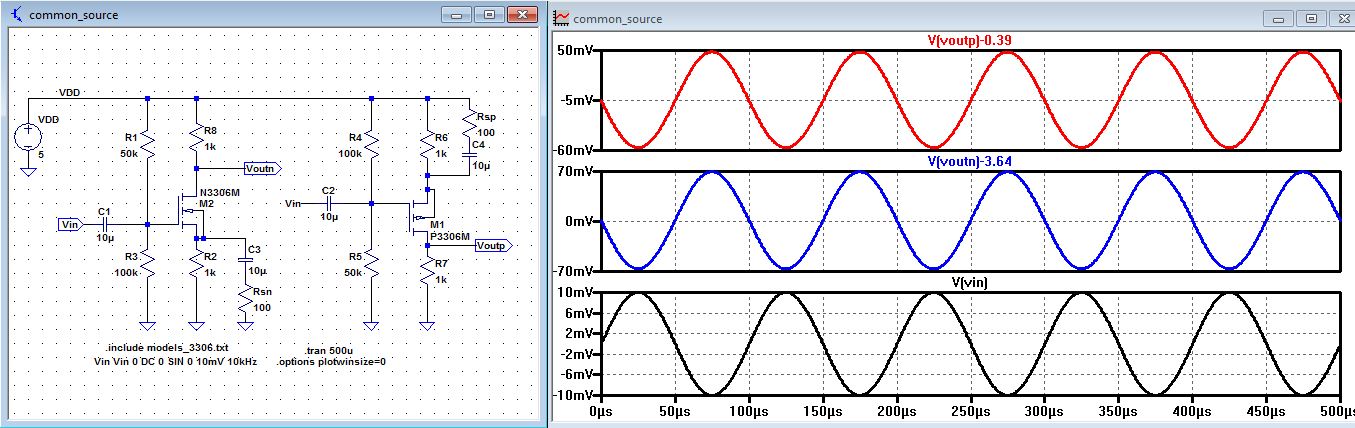
Simulation of a common-source amplifier using LTSpice

From the transient analysis below we can clearly see that the output of Voutn = 50mV and Voutp = 70mV, and Vin. The Gain is Vout/Vin so the gain is 5 for the Pmos and 7 for the Nmos amplifier. This circuit along with the plot was drafted by Dr. Baker used in prelab.

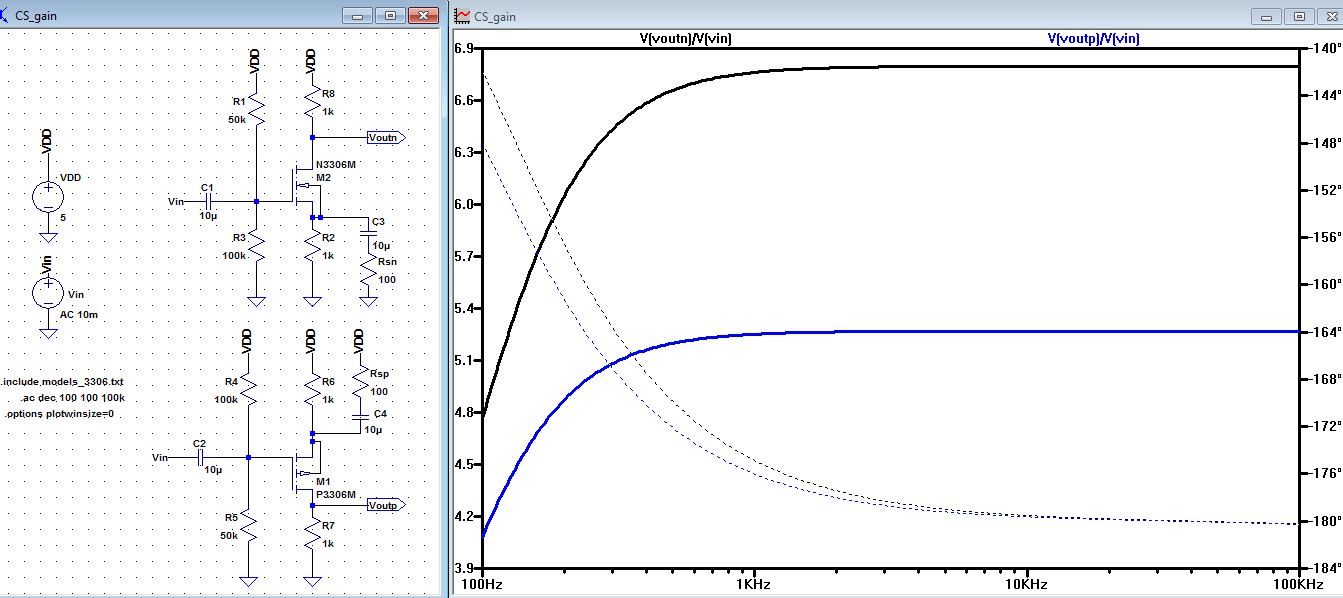
We can also verify the gain using an AC analysis. Below you can see that the gain Voutp/Vin = 5.2 and Voutn/Vin = 6.7 at 10kHz. For the purpose of the lab we can assume that the gain is 5 and 7 respectively. The solid line is the magnitude of Vout/Vin, and the dotted line indicate that phase, as you can see the phase for both Nmos and Pmos is -180 degree.

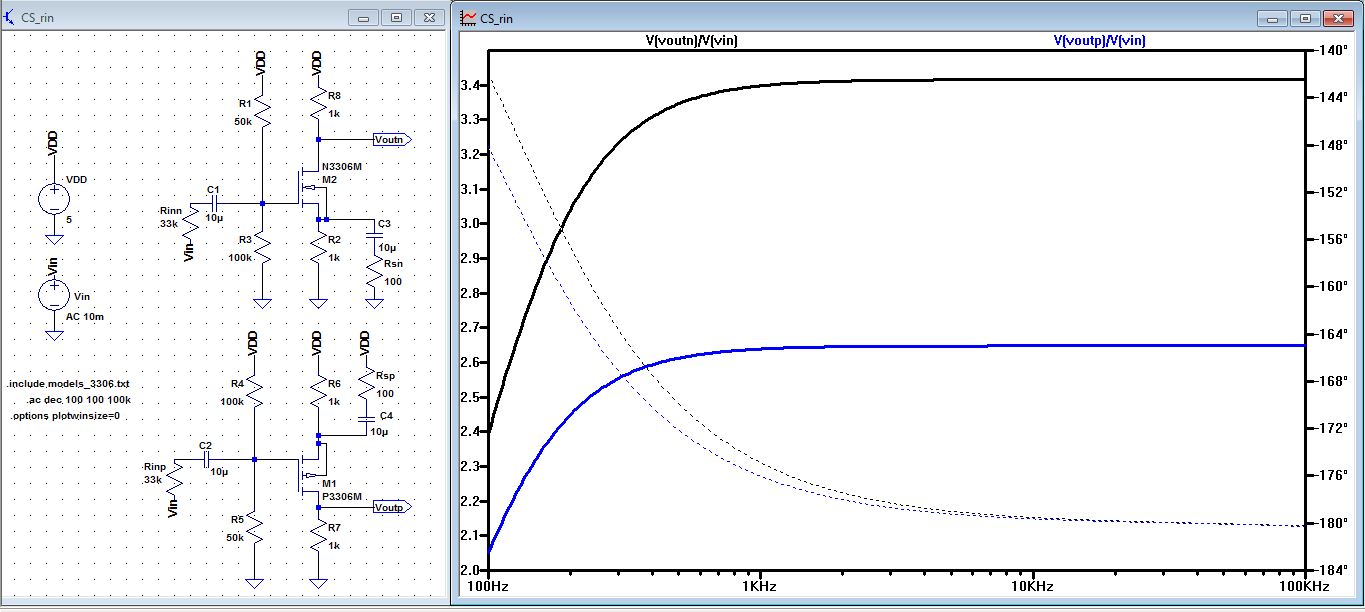
From our hand calculation, we got Rin was 33k Ohms for both the Nmos and Pmos, so in theory if we put a 33k resistor in parallel before the 10u capacitor we should get half of the gain we had from previous simulation. You can see the schematic below a 33k resistor was placed before the 10u capacitor and our new gain is roughtly half of what it was before for both the Nmos and Pmos. This voltage division indicated that our hand calculation of Rin=33k is correct.

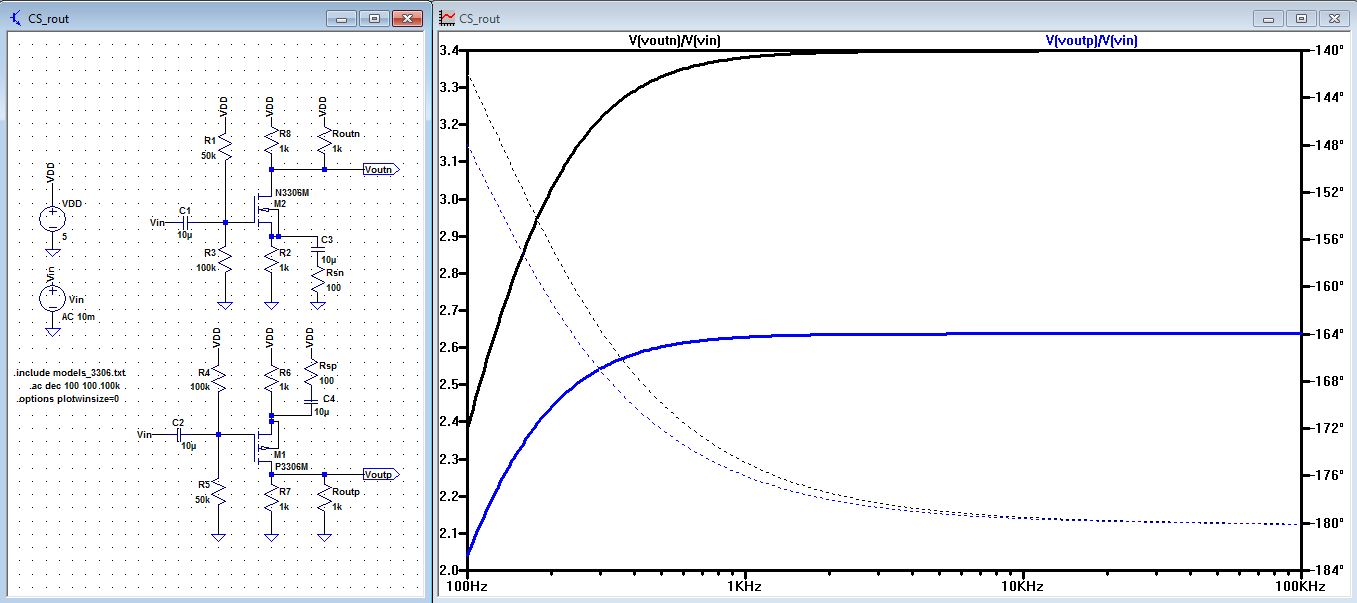
From our hand calculation, we got Rout was 1k Ohms for both the Nmos and Pmos, so if we put a 1k resistor in parallel with R8 for the Nmos, and 1k resistor parallel with R10 for the Pmos we should get half of the gain. As you can see from the schematic below the location of Routn and Routp, and the AC analysis gave us 3.4 for Nmos and 2.6 for Pmos, this is half of our original gain. This voltage division indicated that our hand calculation of Rout=1k is correct.

Experiment of the NMOS and PMOS common-source amplifier
NMOS	PMOS
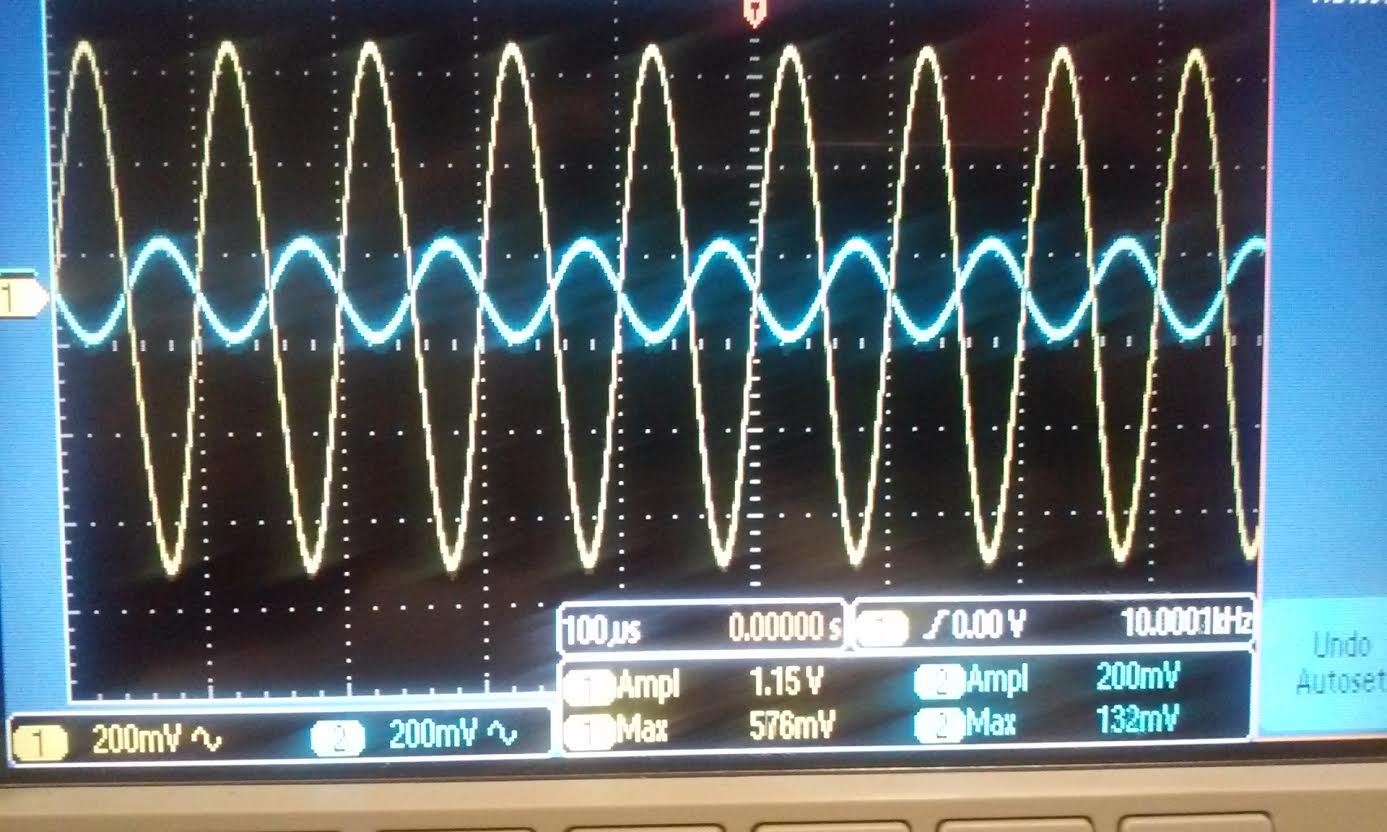
Gain: for the Nmos amplifier the gain is 1.15V/200mV = 5.75. For the Pmos the gain is 336mV/196mV = 1.7. This gain is less than the theoretical values which indicated that the Gm is much smaller than the expect value of 10mA/V. In the data sheet of the ZVP3306A the forward transconductance (gm) operating point is 60mS while our simulation was only 10.7mA/V. it also gave the operating condition for Vds = -18V and id=-200mA. Our Vds operating point was 4.6V and id was only 384uA.

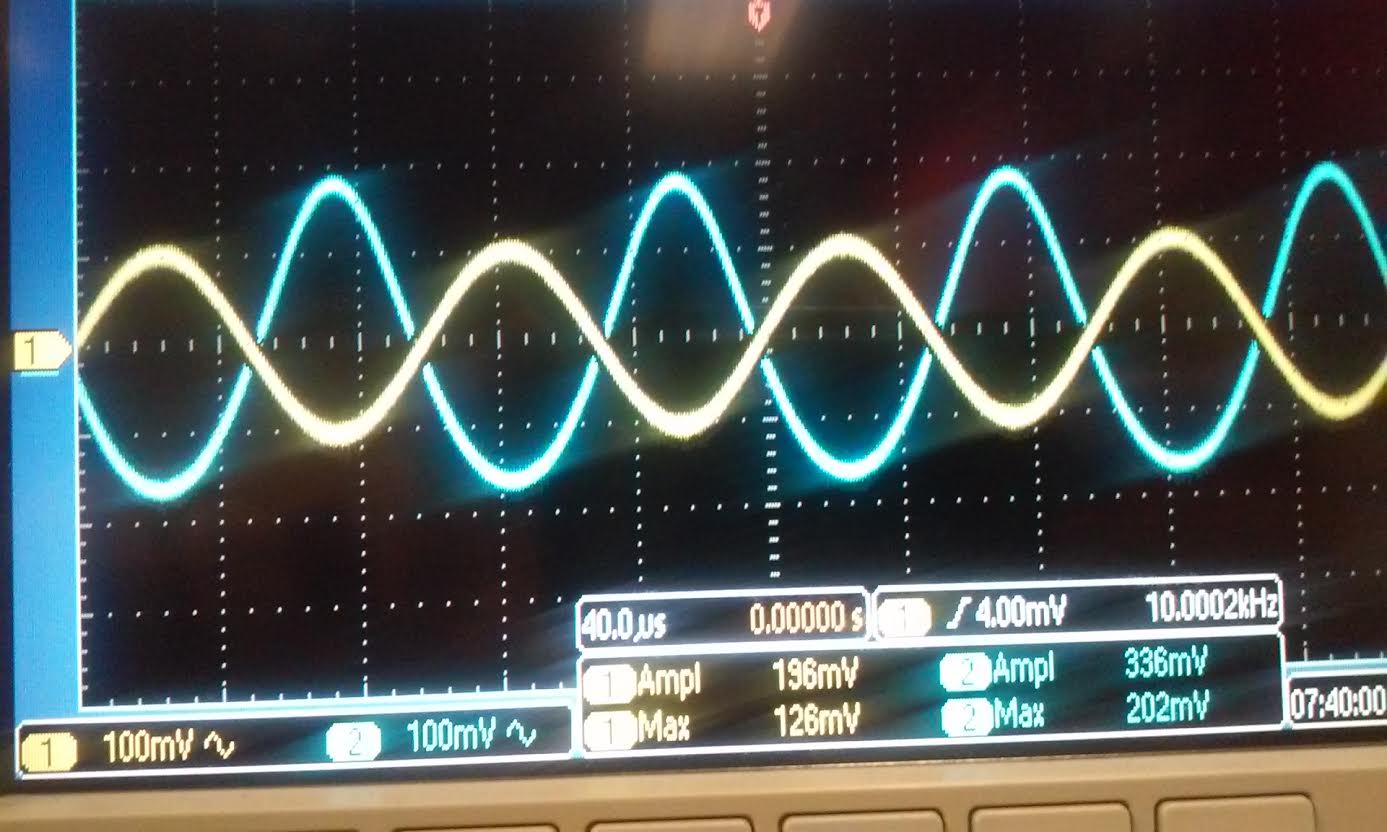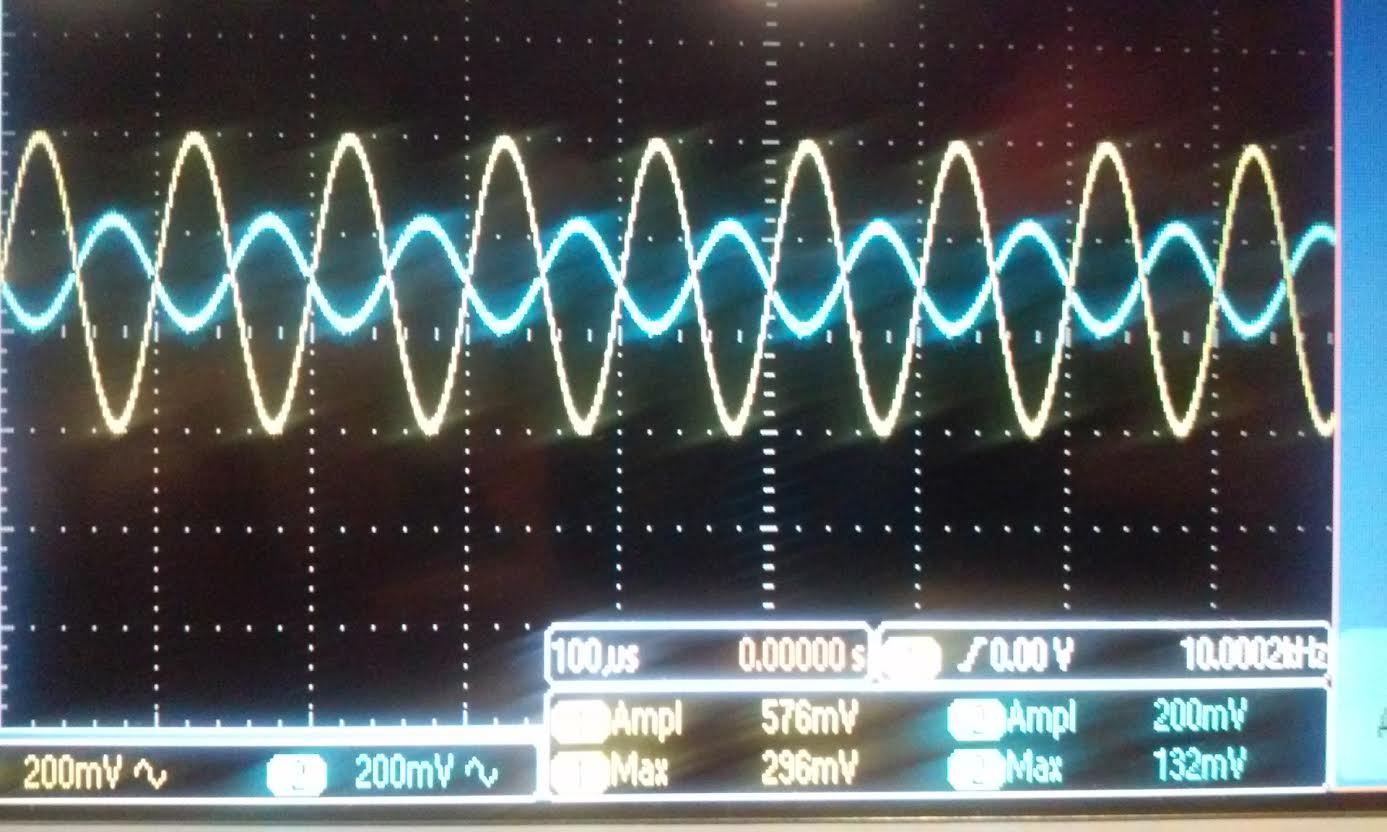
Rin: we used Rin=33k for both the Nmos and Pmos our gain for the Nmos is 576mV/200mV = 2.88, and for the Pmos is 160mV/200mV = 0.8 both value is half of the gain when no resistor was hook up. This indicate that our output resistance is 33k because it divides the original gain in half when the 33k resistor was hooked up.

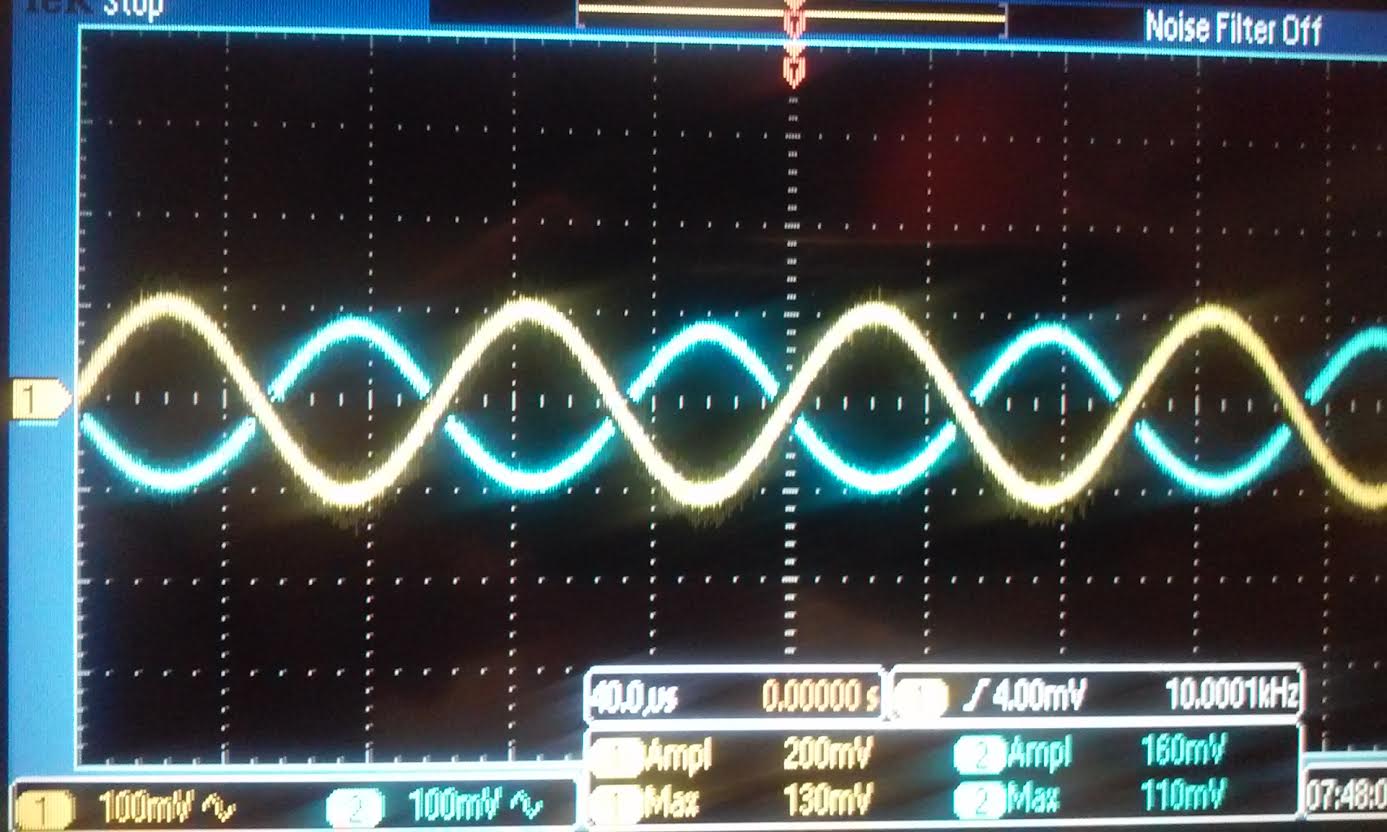Rout: The gain for the Nmos when a 1k resistor is hook up is 544mV/200mV = 2.72, and for the Pmos is 164mV/200mV = 0.82 both of this gain is roughly half of our original gain.

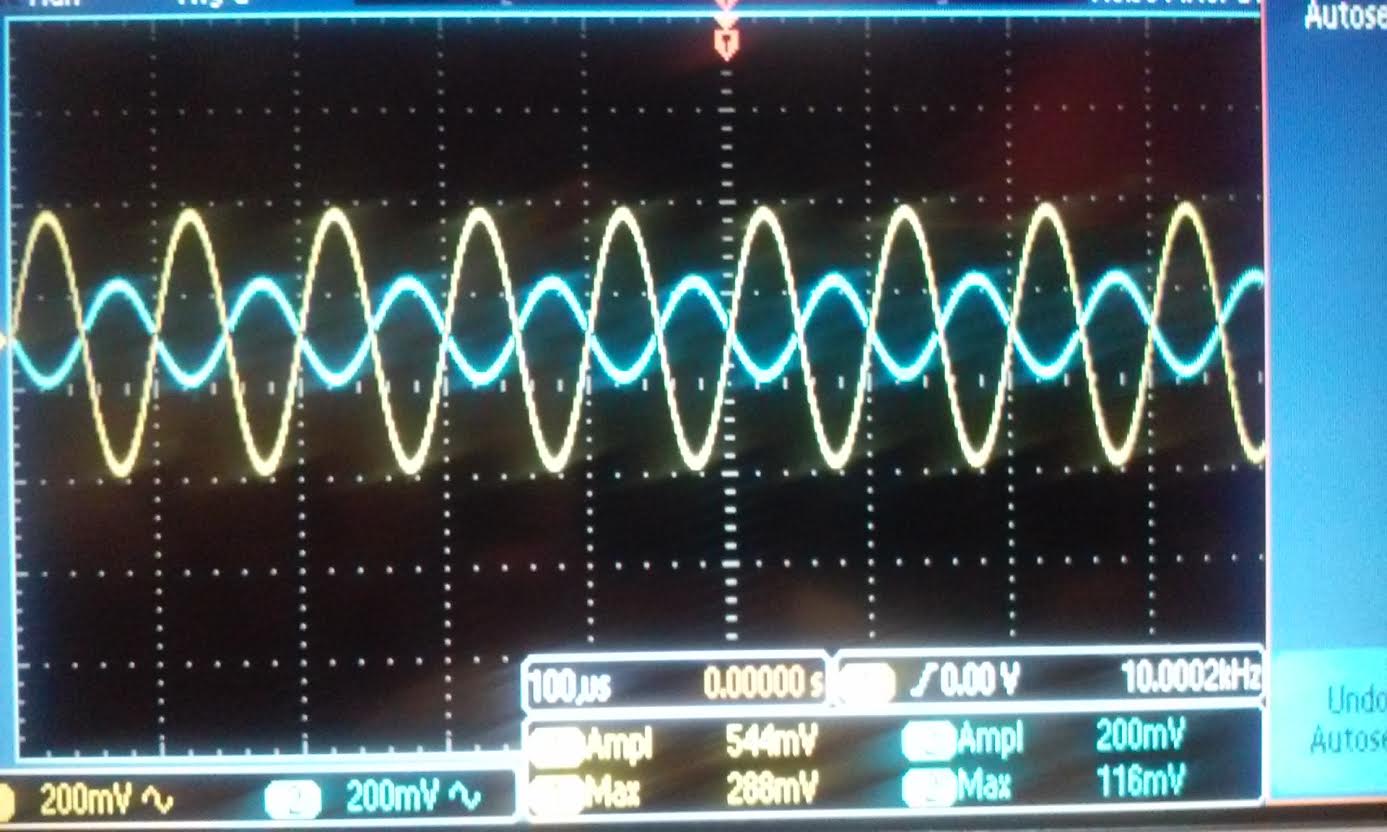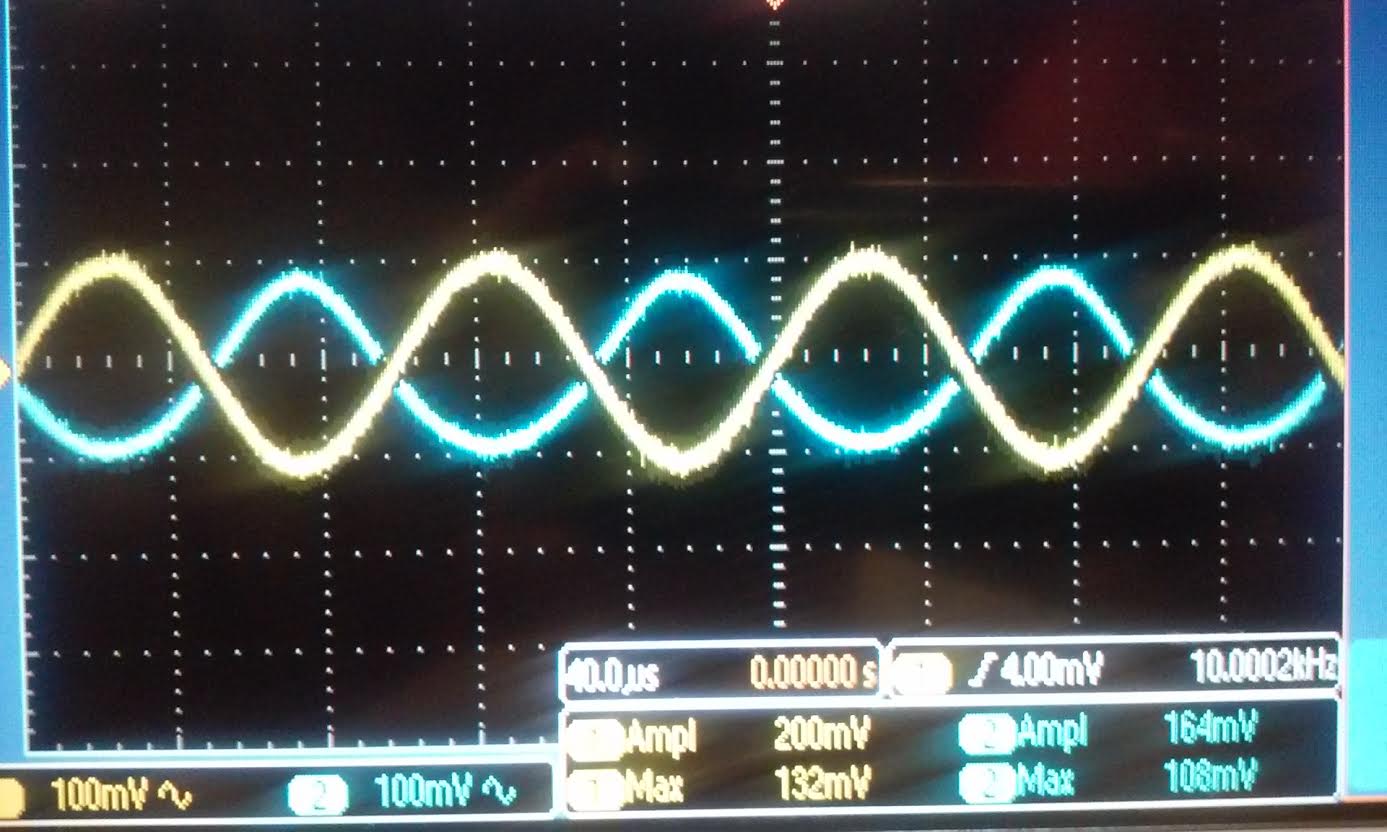Summary: NMOS common-source
	Hand Calculation	Simulation	Experiment
Gain	-6.85	-6.7	-5.75
Rin	33.3k Ohms	33k Ohms	33k Ohms
Rout	1k Ohms	1k Ohms	1k Ohms

Summary: PMOS common-source
	Hand Calculation	Simulation	Experiment
Gain	-5.42	-5.2	-1.7
Rin	33.3k Ohms	33k Ohms	33k Ohms
Rout	1k Ohms	1k Ohms	1k Ohms

Below are two common-gate amplifiers.

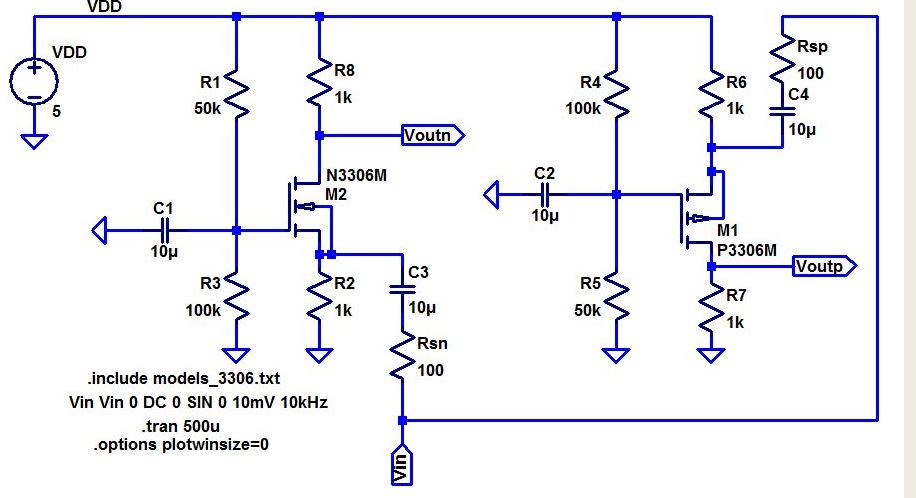
Discuss the operation of these amplifiers in your lab report including both DC and AC operation.

Hand calculate the gains and the input/output resistances.

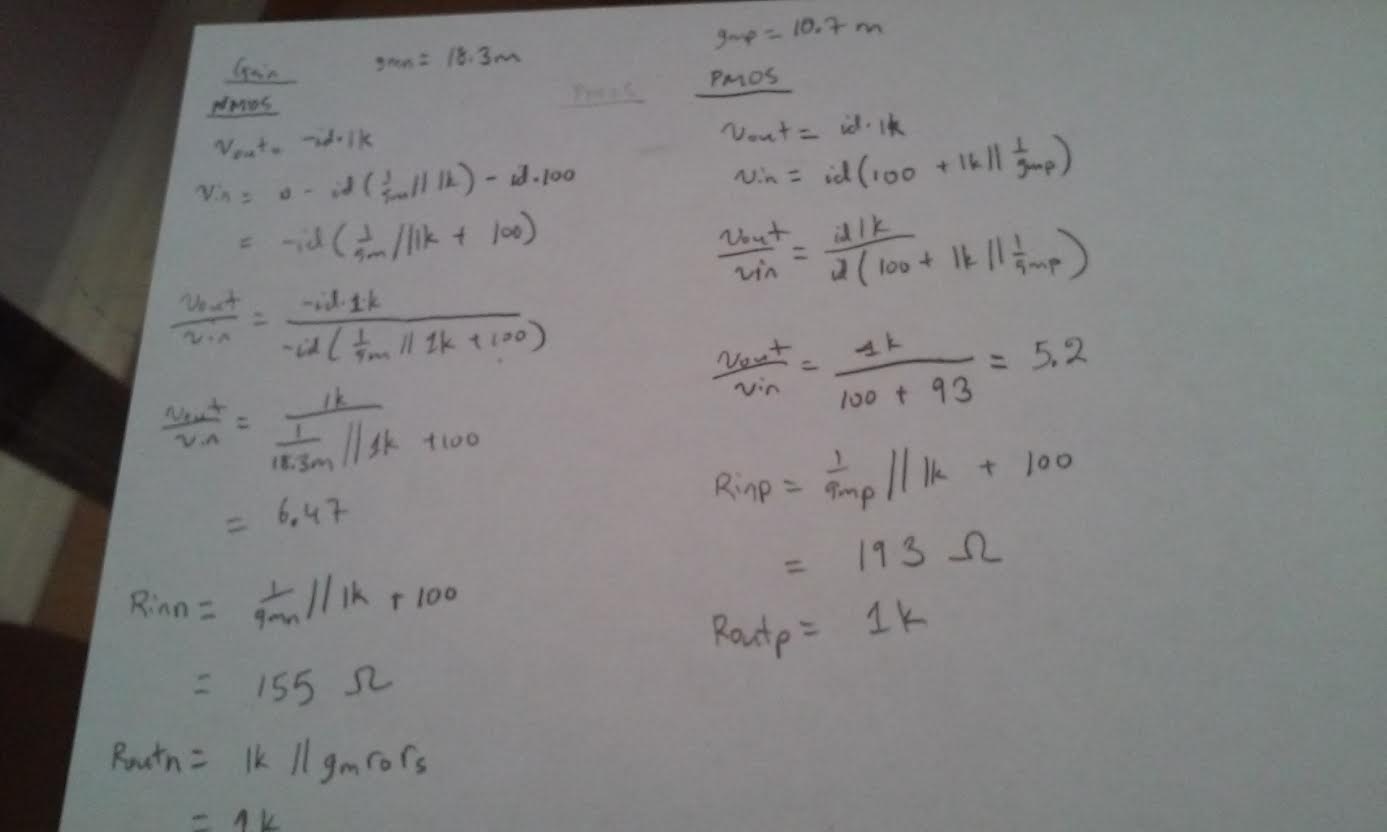
How does the source resistance, Rsn or Rsp, influence the gain.

Similar to the common-source, if you increase Rs, Rsn or Rsp then the gain will decrease.

Again compare your hand calculations to simulation and experimental results.

Simulation of a common-gate amplifier using LTSpice

From the transient analysis below we can clearly see that the output of Voutn = 50mV and Voutp = 70mV, and Vin. The Gain is Vout/Vin so the gain is 5 for the Pmos and 7 for the Nmos amplifier. This has the same gain as the common-source amplifier This circuit along with the plot was drafted by Dr. Baker used in prelab.

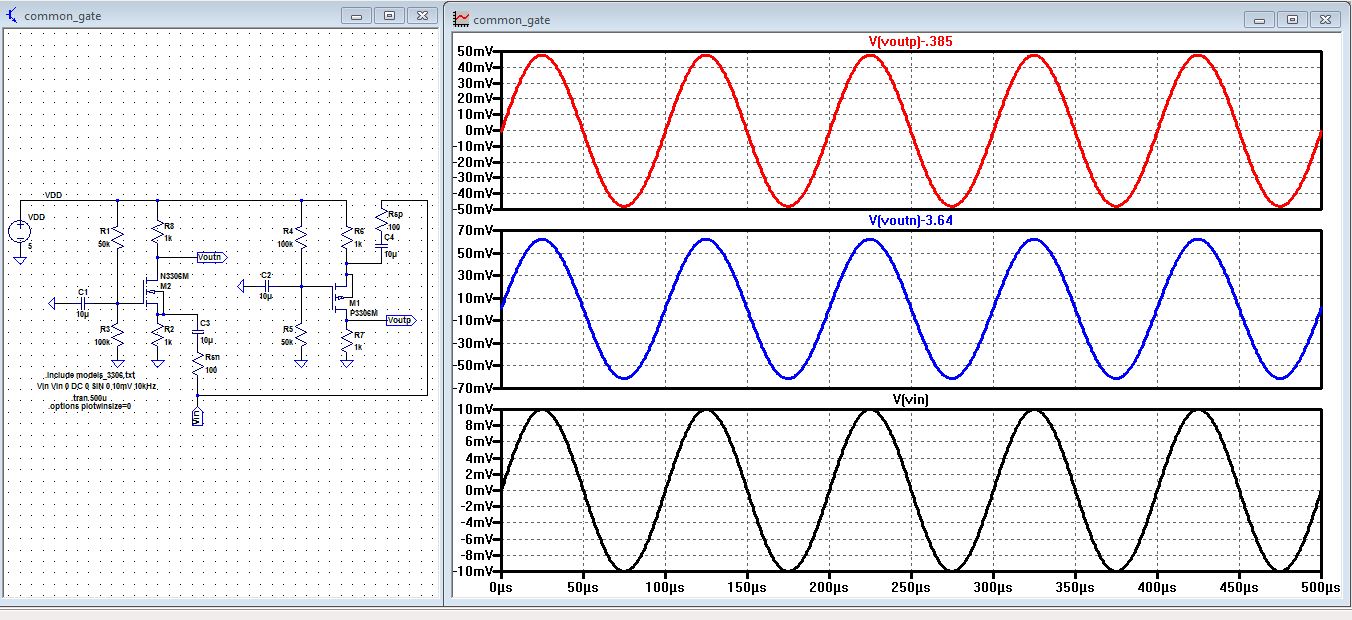We can see from the AC analysis below that the gain for Voutn/Vin = 6.2 and Voutp/Vin = 4.8, and both have a phase of -180 degree at 10 kHz.

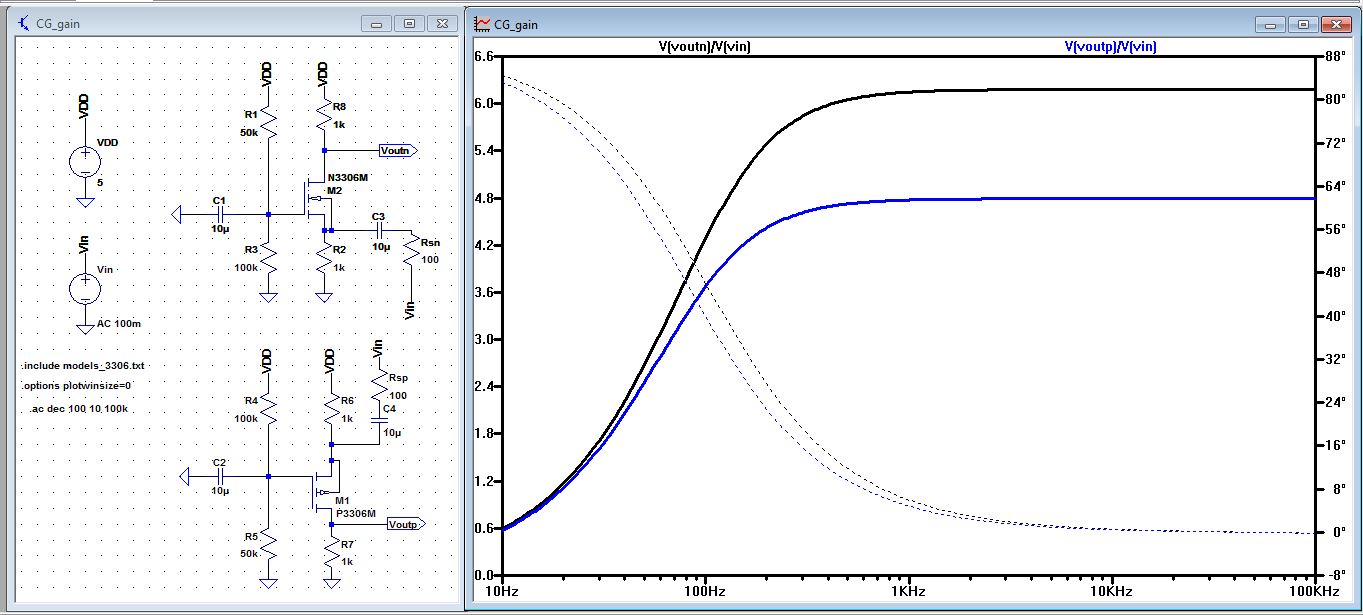Rin: From our hand calculation we got Rinn=155 Ohms, and Rinp=193 Ohms, we use that resistor and hook it up before the Rsn and Rsp, and our gain is 3.1 for the Voutn/Vin and 2.4 for Voutp/Vin which is half of the original gain without the divider.

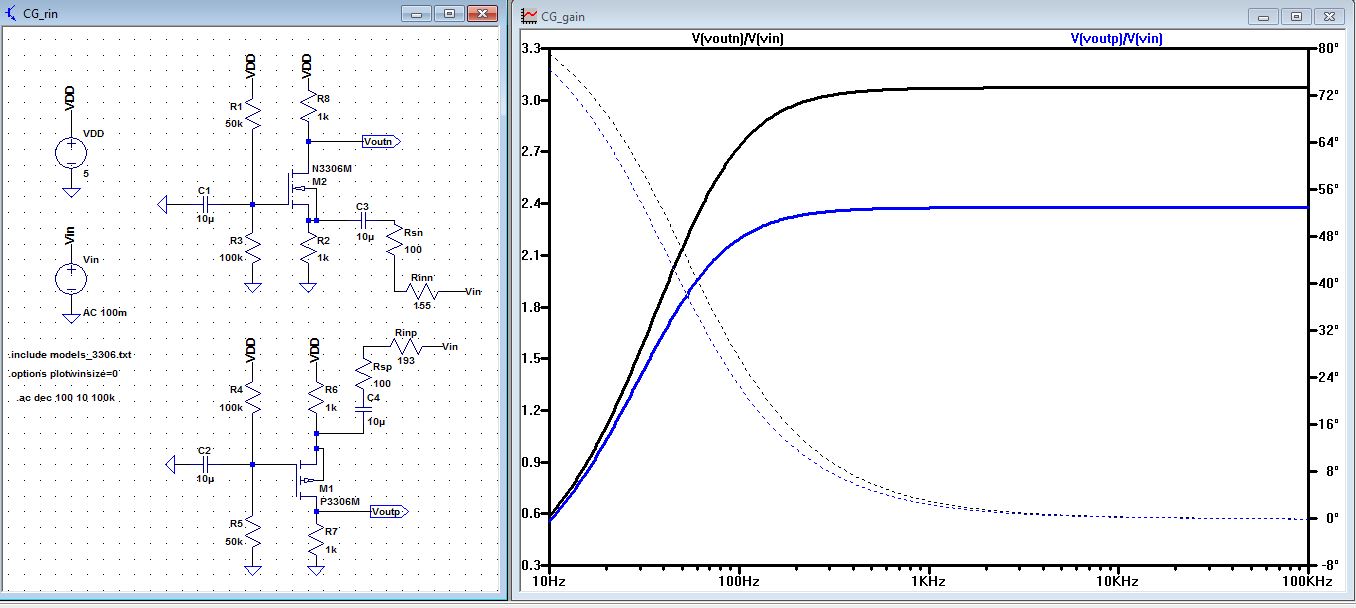Rout: we calculated Rout and it was 1k for both the Pmos and Nmos, so we put a 1k resistor parallel to the R8 and R7 and our gain is 3.1 and 2.4 which is half of our original Gain, as you can see from the AC analysis below.

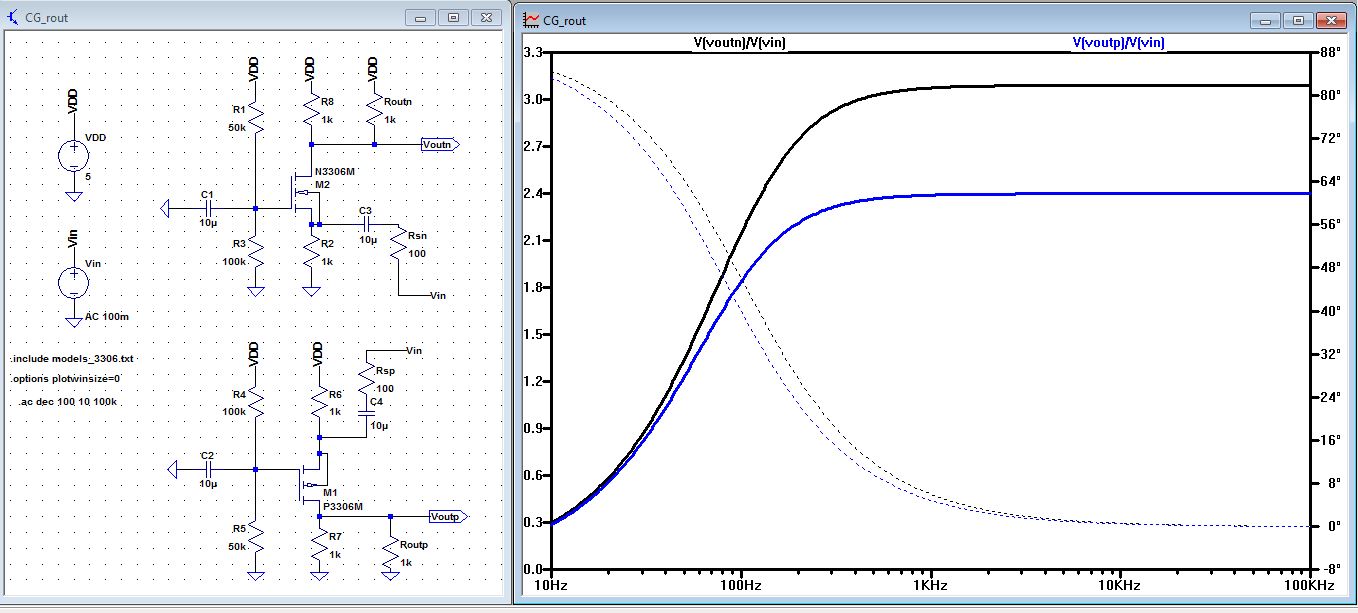Experiment of the NMOS and PMOS common-gate amplifier
NMOS	PMOS
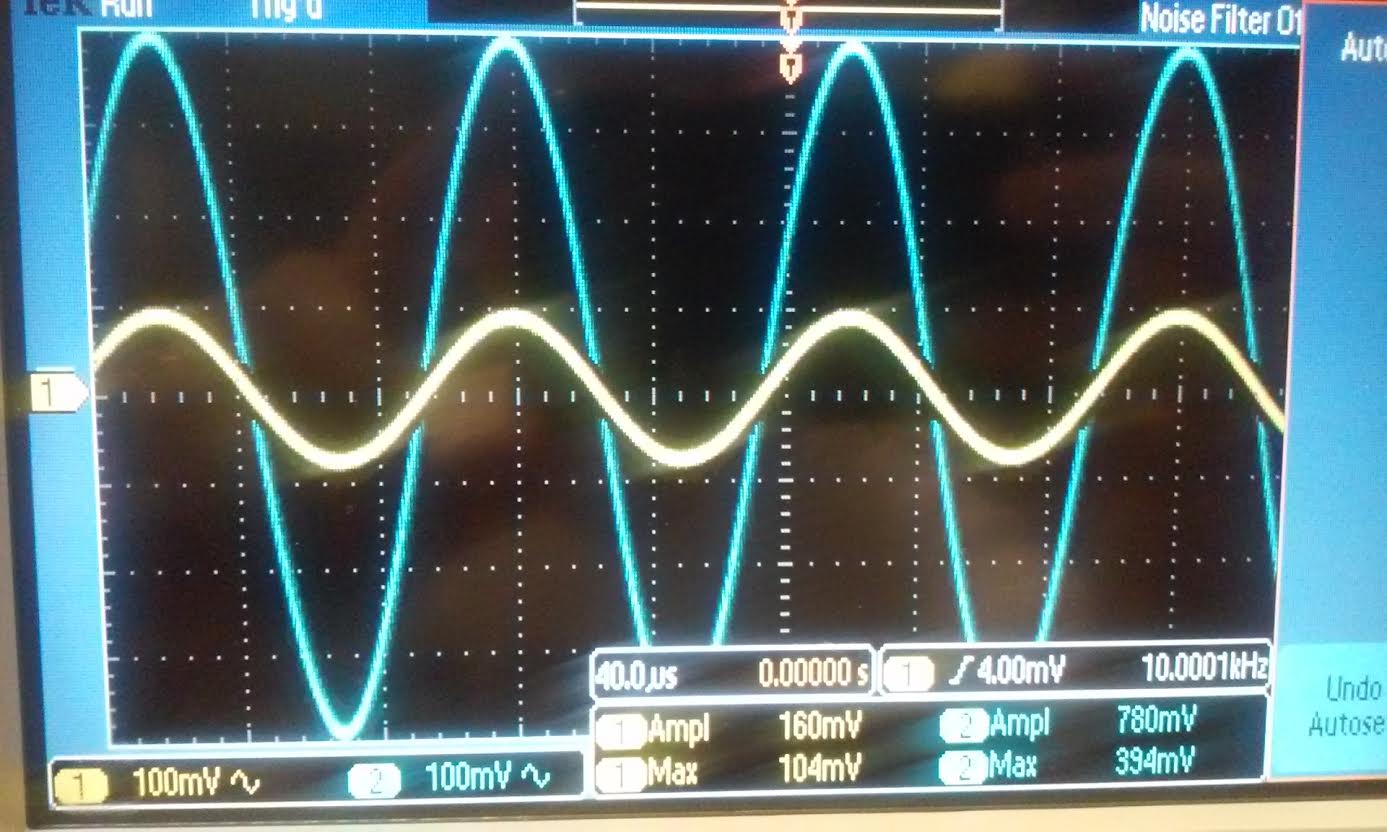
Gain: for the Nmos amplifier our experimental gain was 780mV/160mV = 4.9, for the Pmos the gain is 400mV/156mV = 2.56. Our input was 100mV at 10kHz. In the data sheet of the ZVP3306A the forward transconductance (gm) operating point is 60mS while our simulation was only 10.7mA/V. it also gave the operating condition for Vds = -18V and id=-200mA. Our Vds operating point was 4.6V and id was only 384uA.

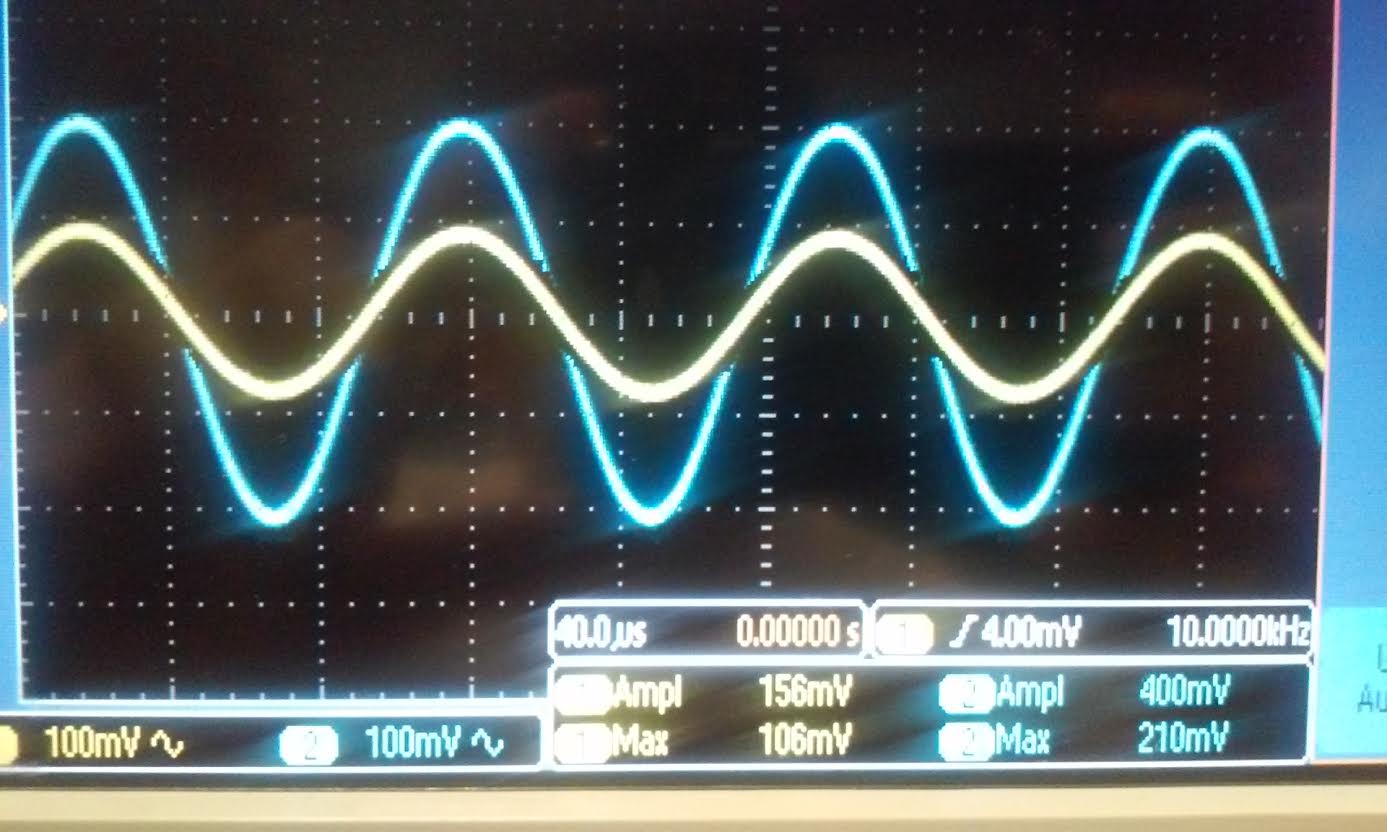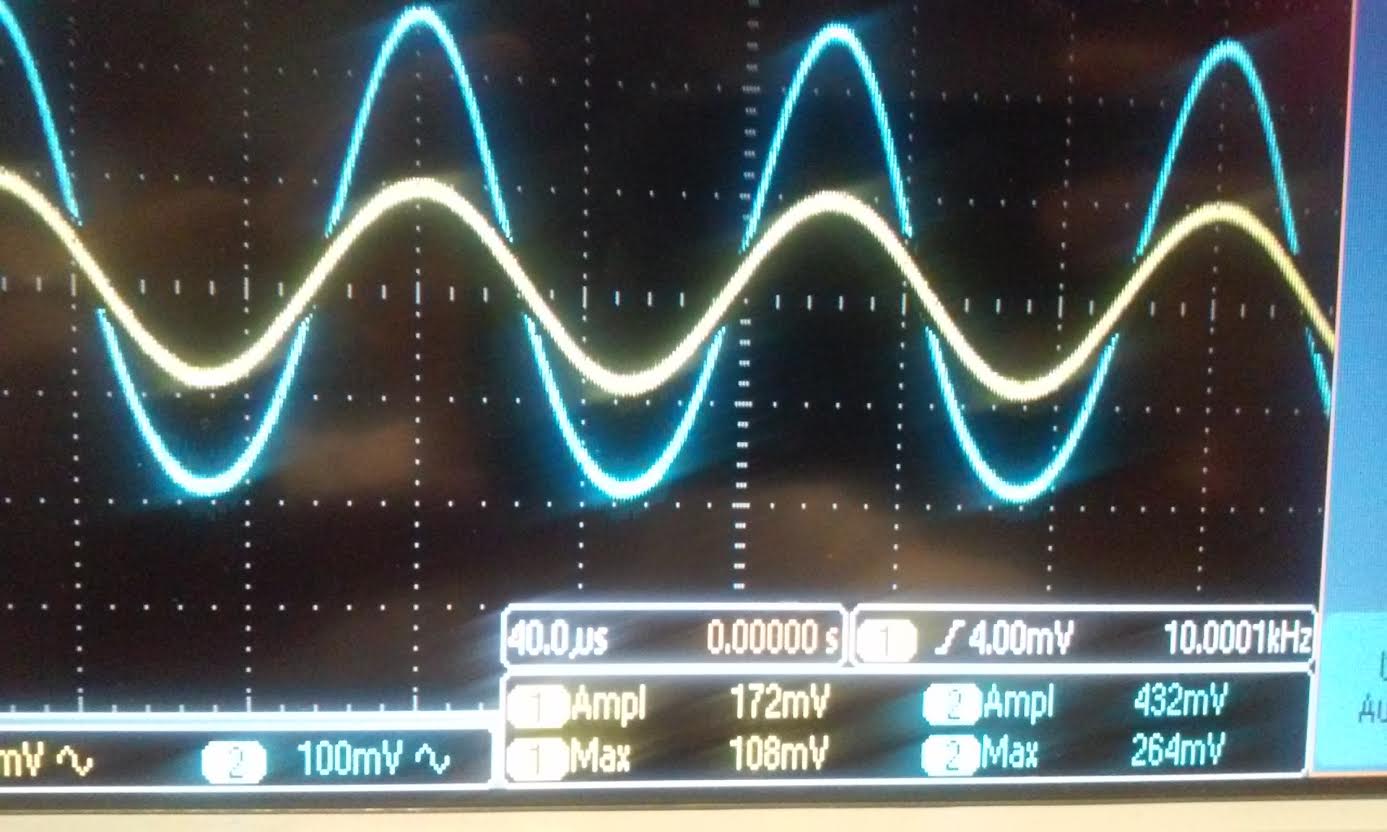
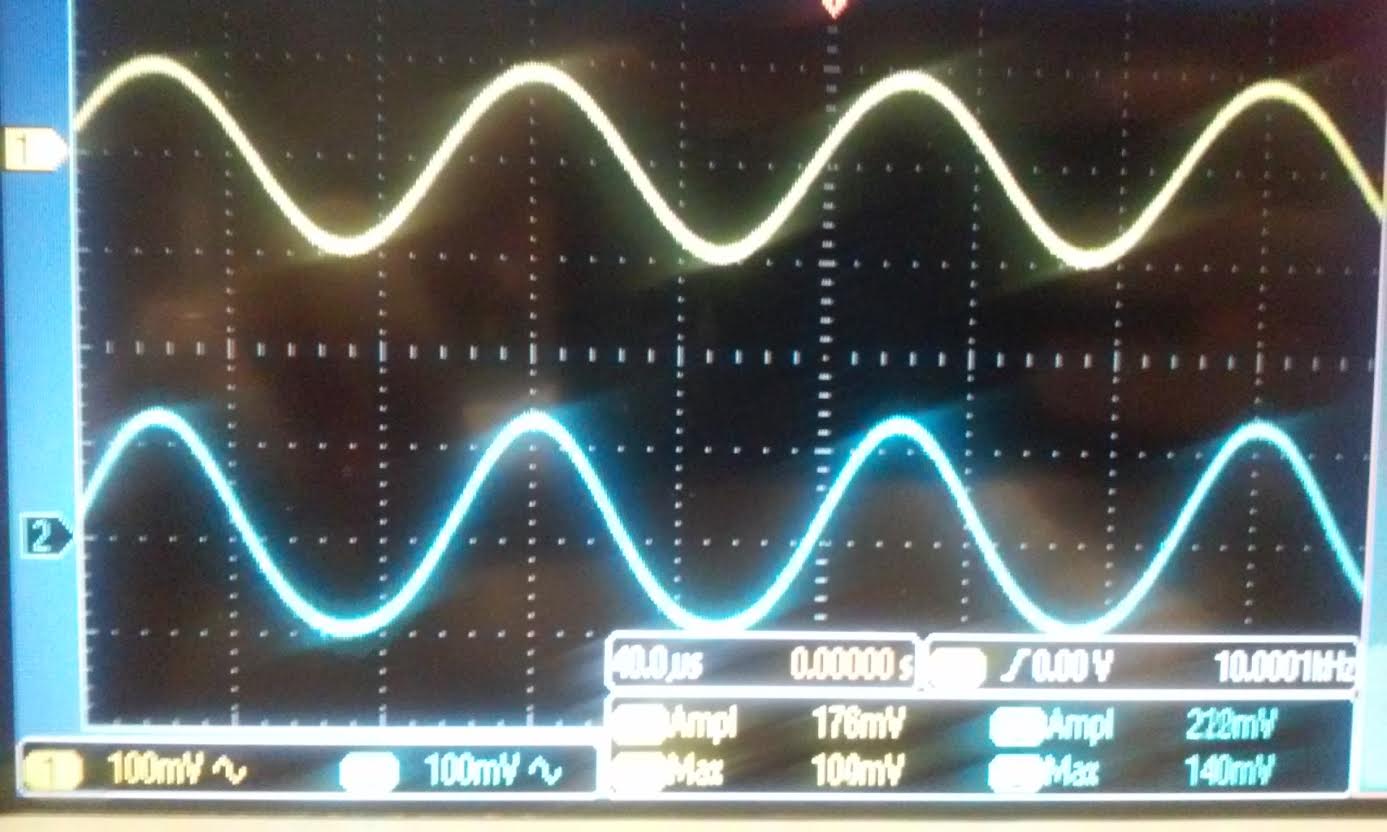
Rin: For the Nmos we used a 162 Ohms resistor and our gain was 2.5, for the Pmos we used 620 ohm resistor and our gain was 212mV/192mV = 1.10. the gains for the Nmos and Pmos is half of our experimental data above.

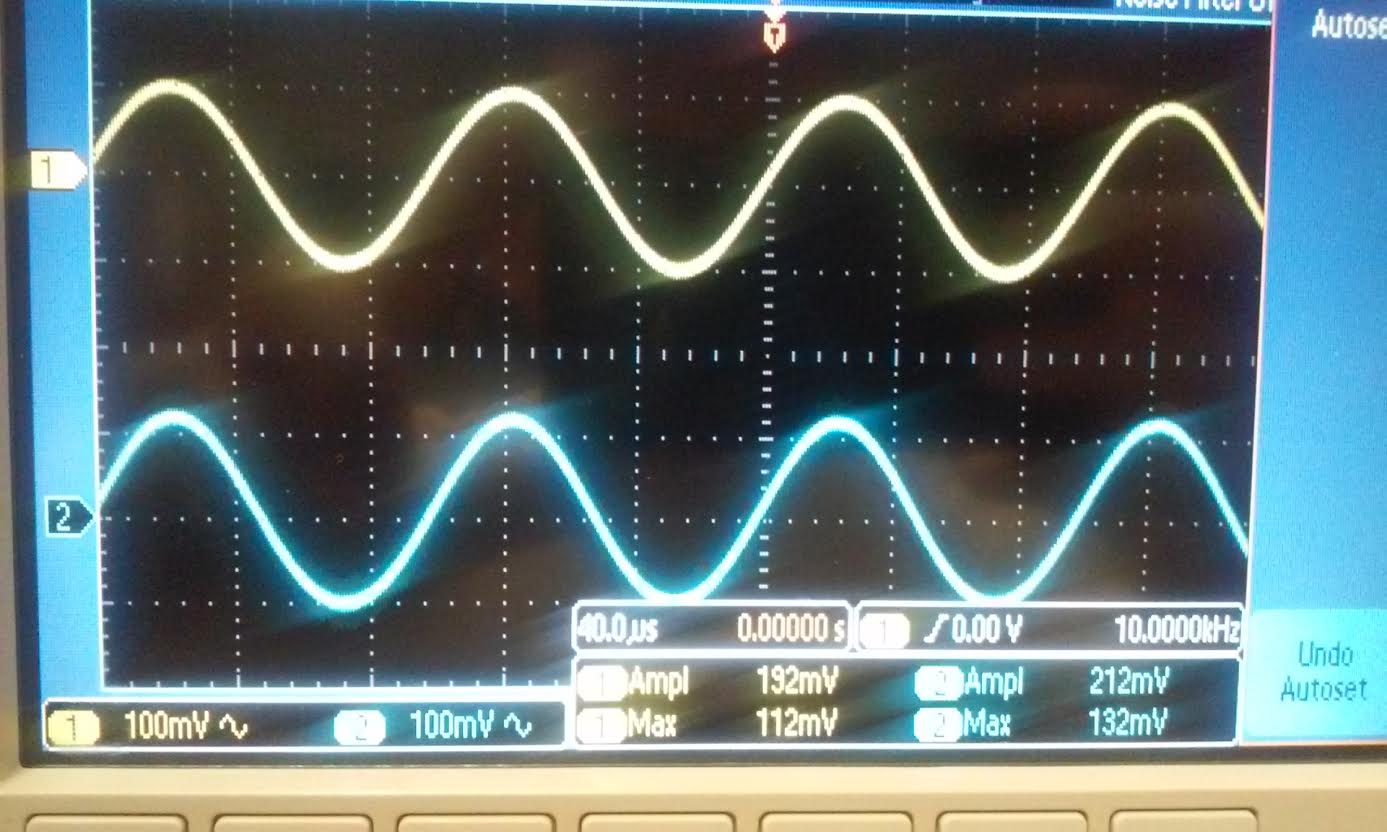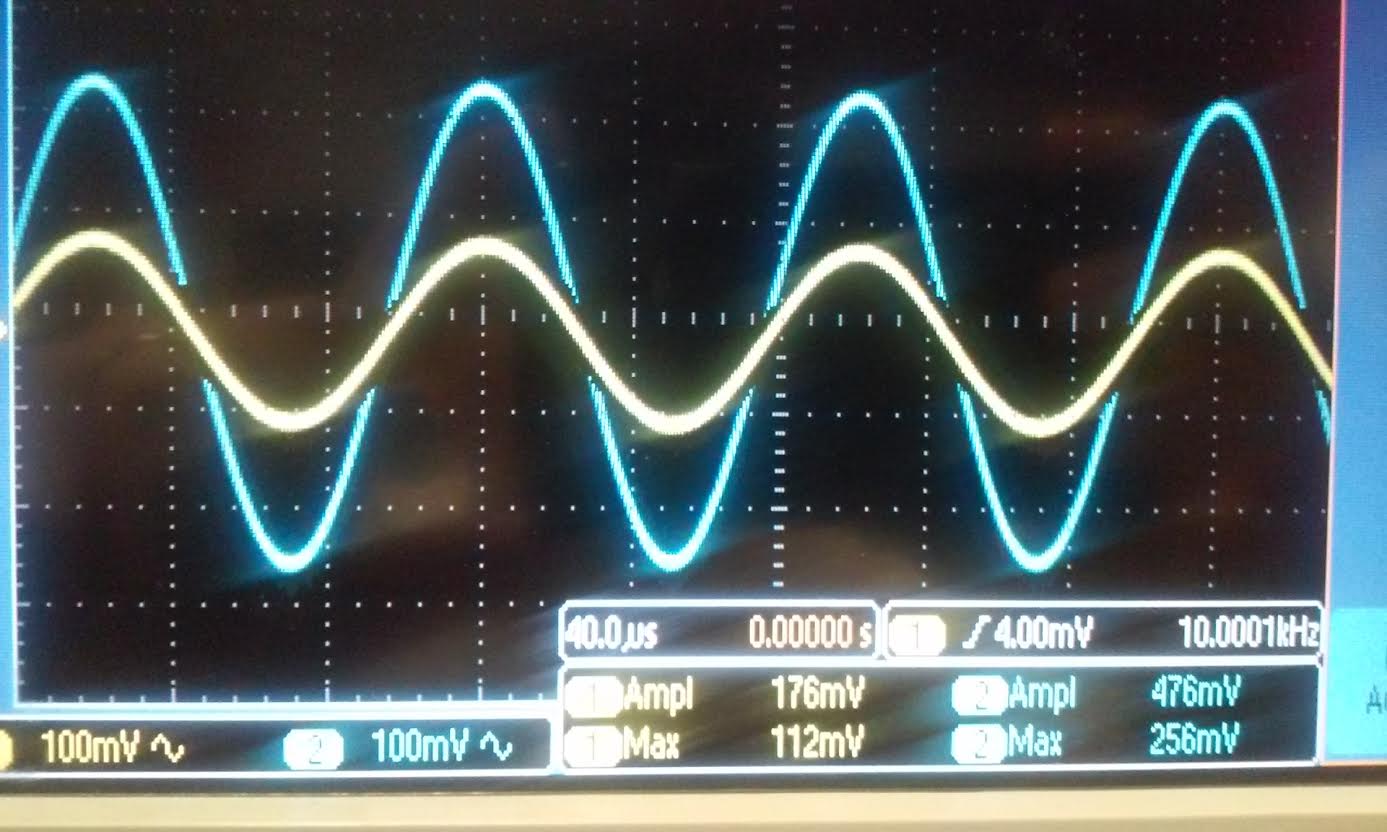
Rout: For the Nmos we used a 1k resistor and the gain was 476mV/176mV = 2.7. For the Pmos we used a 1k resistor and our gain was 218mV/176mV = 1.24. Both of these values is half of our gain of 4.9 for the Nmos and 2.56 for the Pmos.

Summary: NMOS common-gate
	Hand Calculation	Simulation	Experiment
Gain	6.47	6.2	4.9
Rin	155 Ohms	155 Ohms	162 Ohms
Rout	1k Ohms	1k Ohms	1k Ohms

Summary: PMOS common-gate
	Hand Calculation	Simulation	Experiment
Gain	5.2	4.8	2.56
Rin	193 Ohms	193 Ohms	620 Ohms
Rout	1k Ohms	1k Ohms	1k Ohms

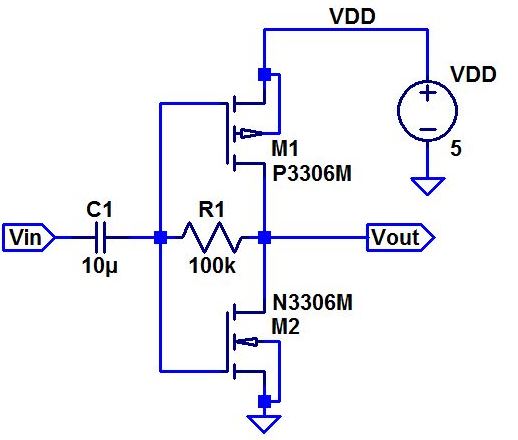
Below is a push-pull amplifier.

Discuss the operation of this amplifier in your lab report including both DC and AC operation.

For DC analysis since Vout and Vin are connected in series with the BIG capacitor and BIG resistor so Vout = Vin, the circuit can self biased because of the BIG resistor thus no DC current flows in the gate. For AC, Rin = Rout = 100k, assuming the gate resistance is infinitely large.

Hand calculate the gain of this amplifier.

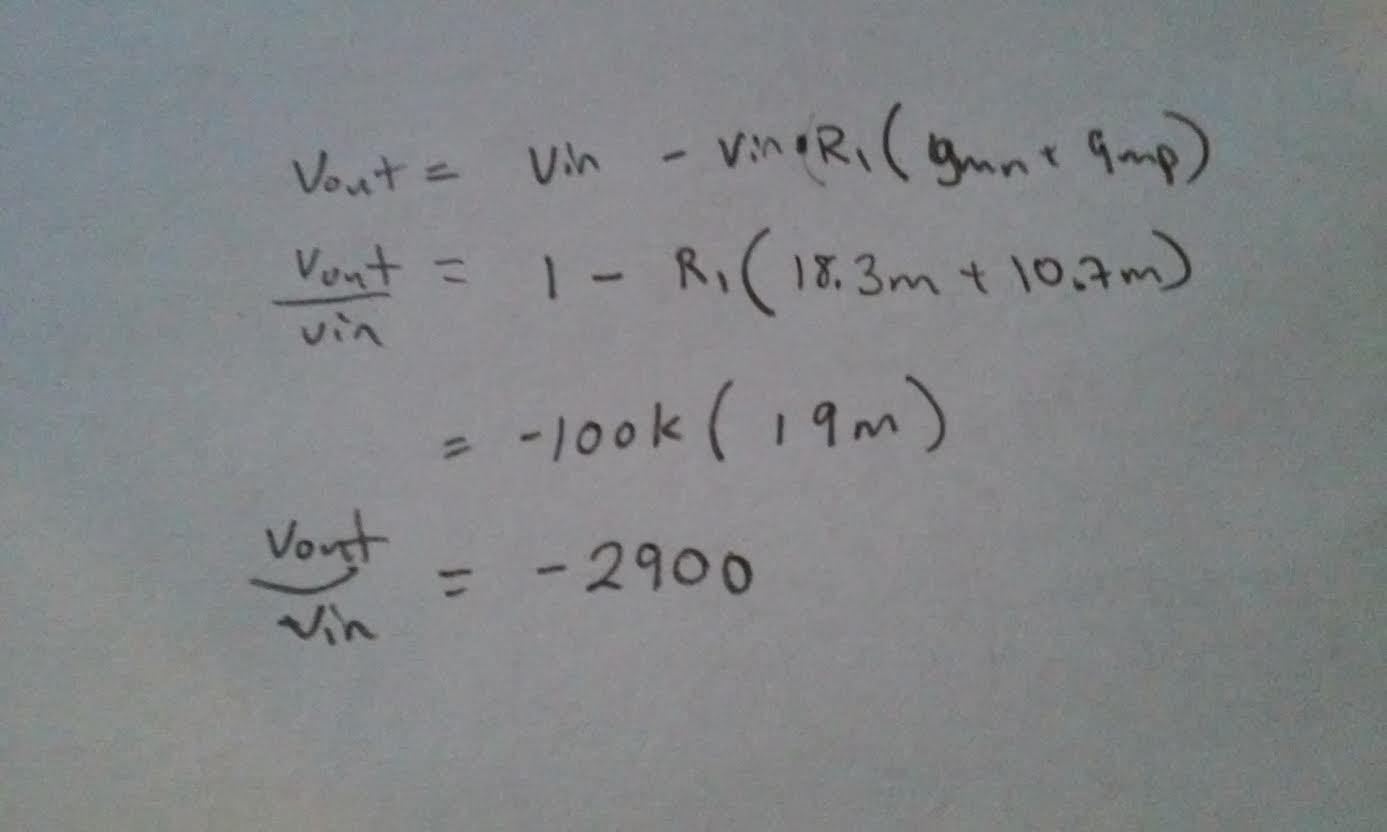
Do you expect this amplifier to be good at sourcing/sinking current? Why or why not?

Well depends on the value of VDD, this circuit can source its current to VDD while it can sink to gnd always. if you think about it the current at the output will be greater than the current at the input. If you have a pulse signal coming in then when the pulse is 0 the circuit will source to VDD and when the pulse is at 1 the circuit will sink the current to GND.

What happens to the gain if the 100k resistor is replaced with a 510k resistor? Why?

If you increase R1 to 510k then the gain will be 5 times larger because of the equation of the gain above.

Again compare your hand calculations to simulation and experimental results.

Note that the gain of this amplifier is large so the output may saturate at VDD and Ground. To avoid this saturation you can reduce the AC input voltage using a voltage divider.

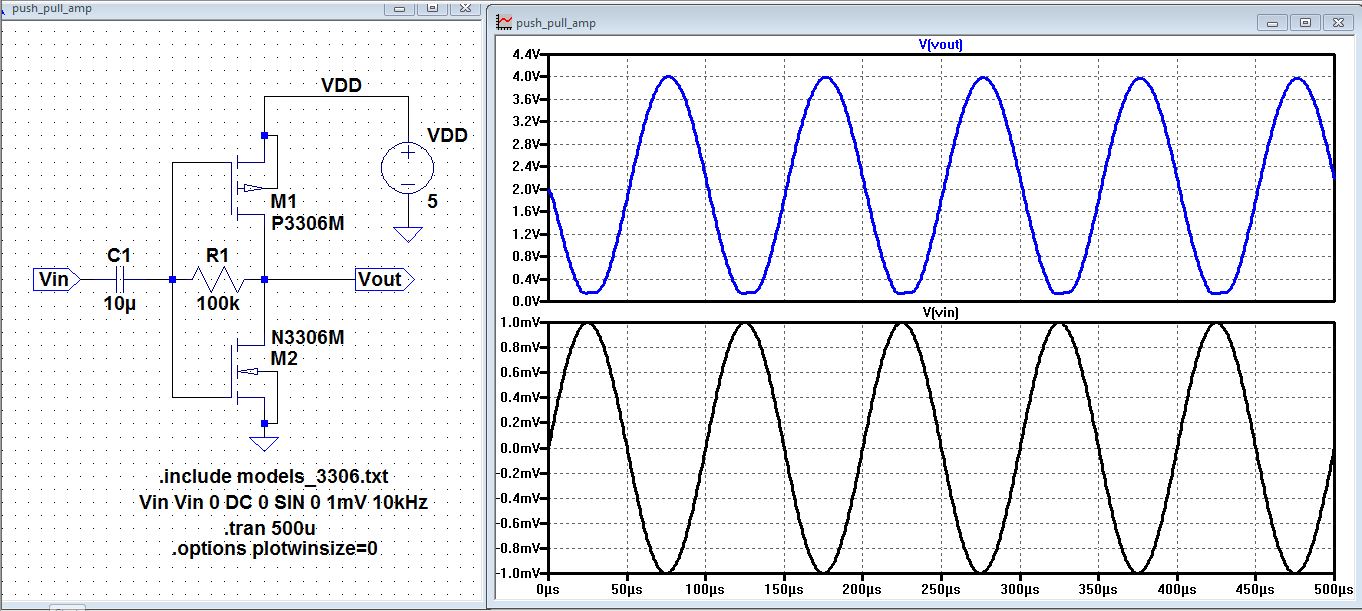
Simulation of a push-pull amplifier using LTSpice

The schematic below was drafted by Dr. Baker and it shows that the gain is 2V/1mV = 2000 using the transient analysis. where R1=100k

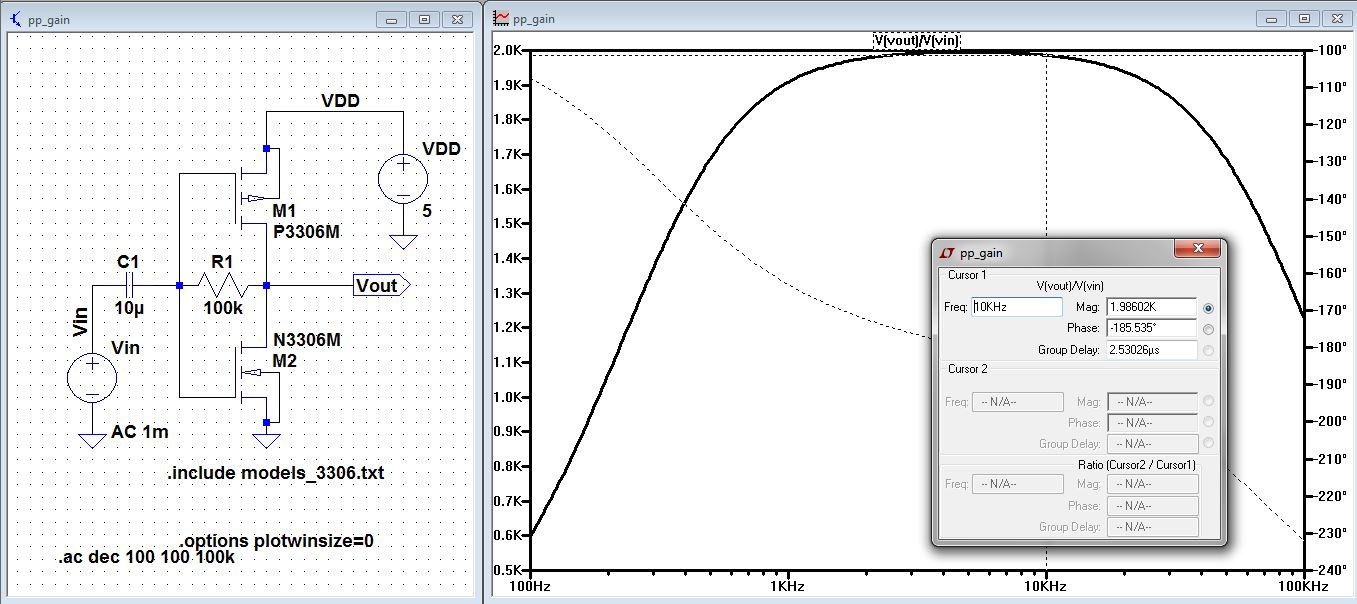
Using the AC analysis at 10 kHz you can see that the gain Vout/Vin = 2k, R1 = 100k

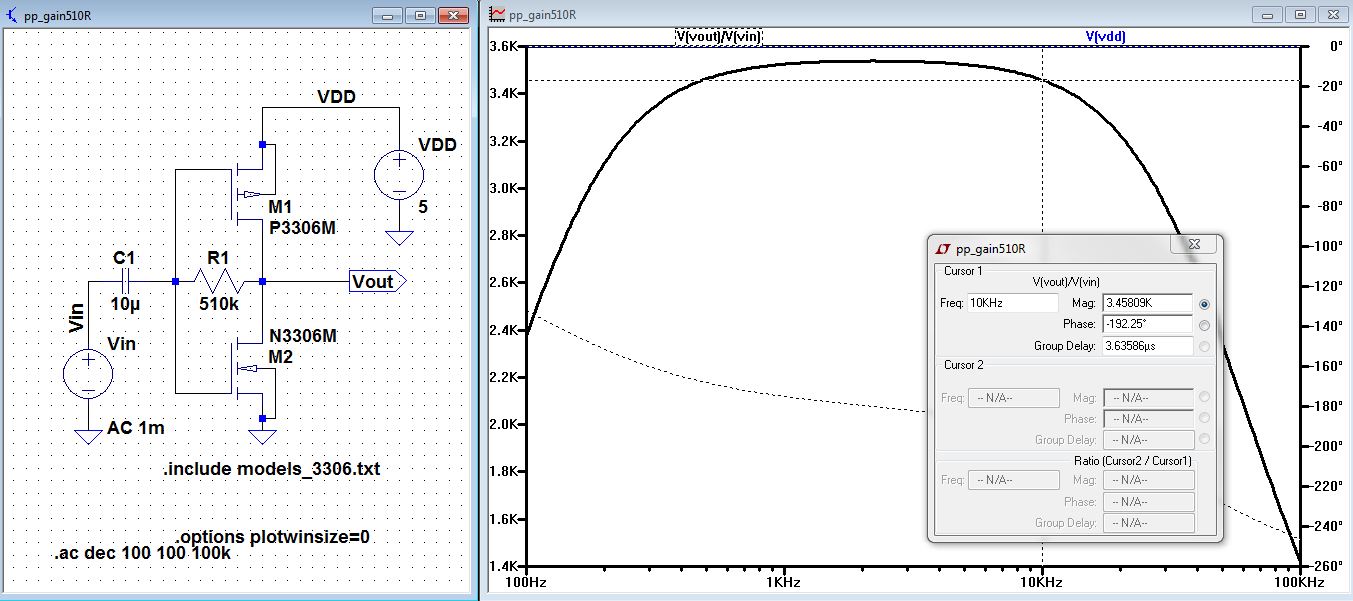
When we put in 510k for R1 we expected it to be 5 times larger than when it was at 100k but the gain is only 3.4k.

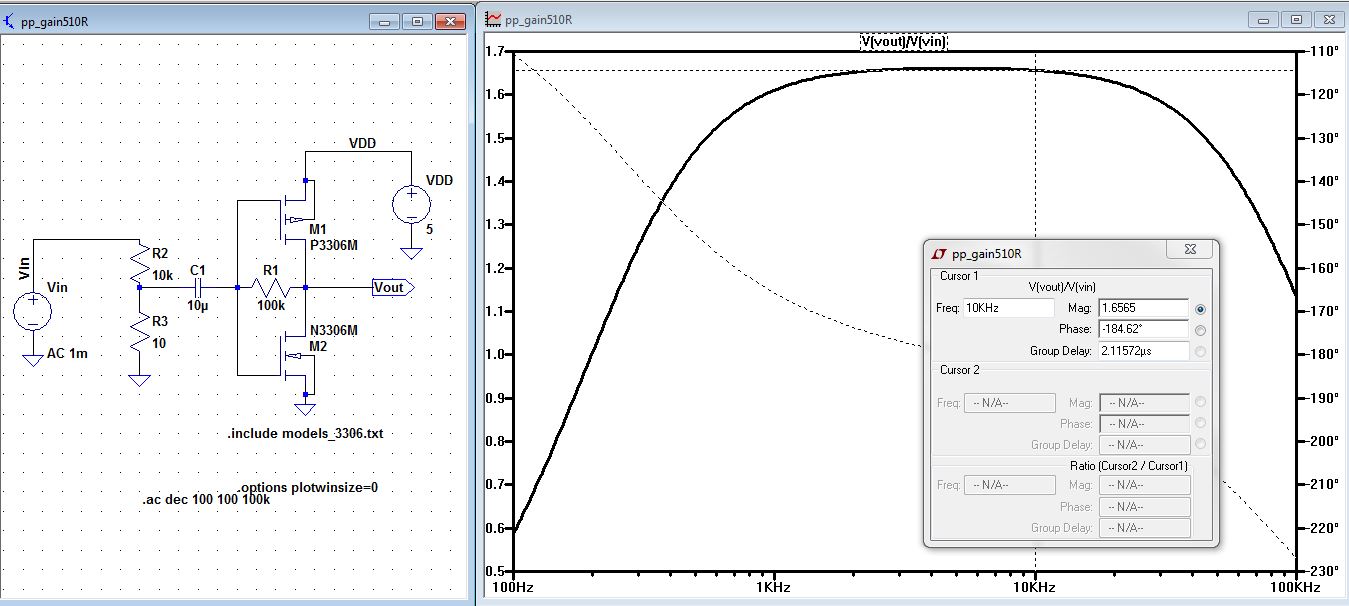
Voltage divide the input by 1000 with a 10k and 10 ohms resistor, as was expected the gain is now 1.65 instead of 2k.

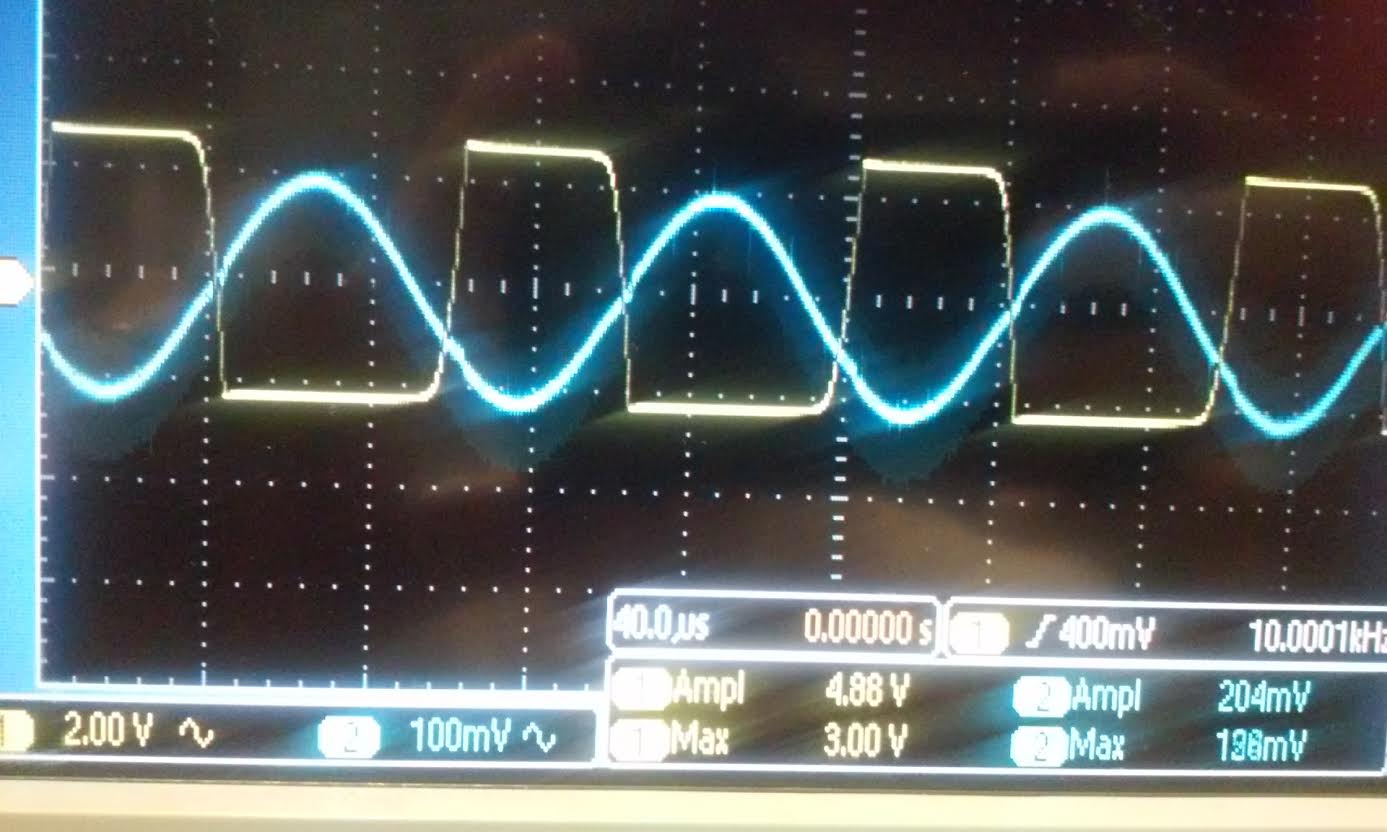
Experimental: Push-Pull amplifier
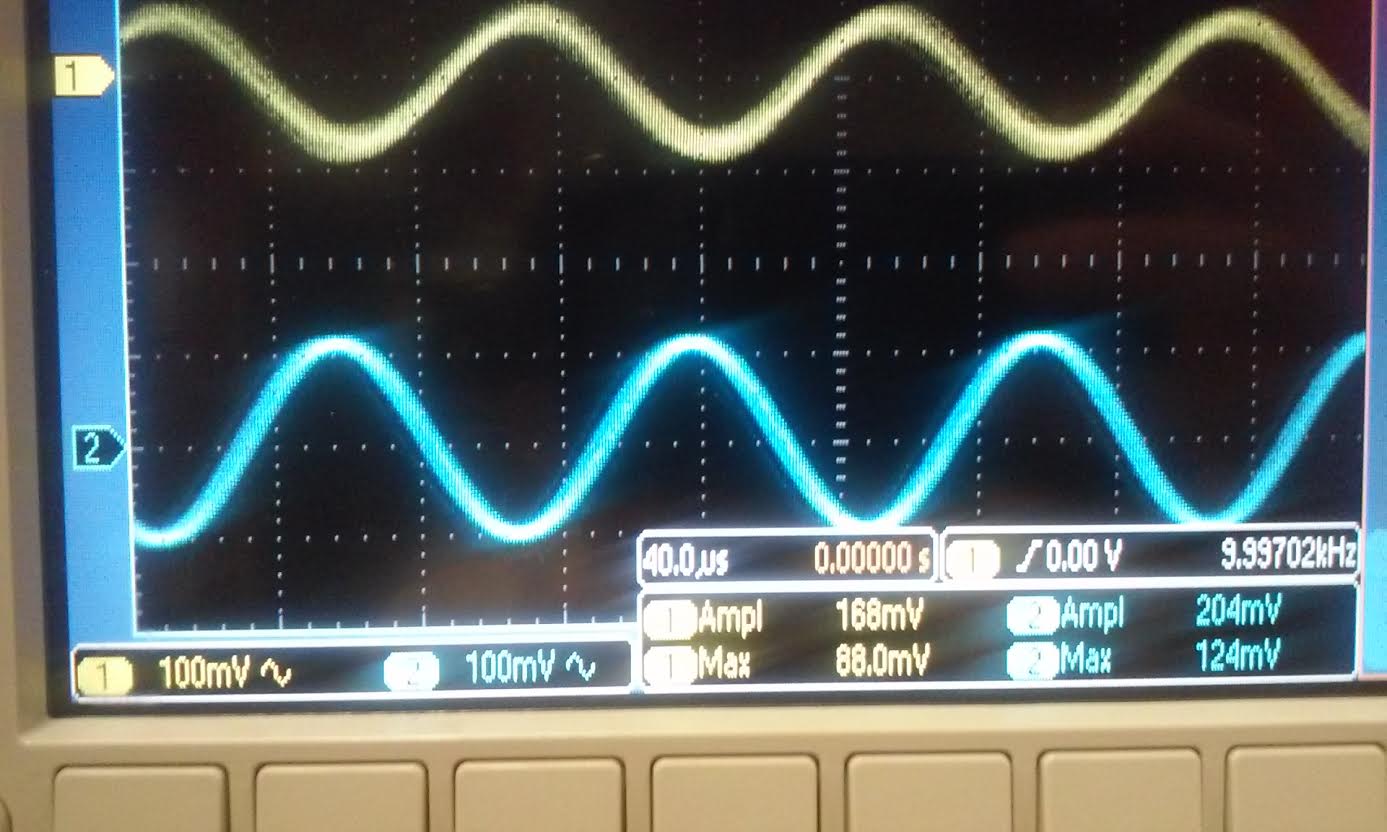
Gain with no voltage divider. As you can see from the scope reading the output can only push to GND and pull to VDD it cannot go beyond VDD. that is why you see a cut-off when the gain reaches near VDD.SInce its hitting the rail at VDD you cannot see the real gain of the ampligier this way.	Gain with 10k and 10 Ohm voltage divider at Vin. we hook up the circuit similar to the schematic above and we got 168mV Vin with a 100mV input. this indicate that our real gain is 1000*168mv=1.68k.

Summary: Push-Pull amplifier
	Hand Calculation	Simulation	Experimental
Gain	-2.9k	-1.99k	-1.68k

Conclusion: Our first experiment involves the source follower amplifier, we found that both the gain for the Nmos and Pmos was 1, to measure Rin we added the calculated Rin and put it after the input but before the 10u capacitor as seen in the schematics. to measure the Rout we used the calculated value and put it in parallel to the output. For the Common-source amplifier the calculated gain for the Nmos was 7, the gain for the Pmos was 5. Both had a phase shift of -180 degree which indicate that the gain is negative for the experiment and and simulation result. For the Common-gate amplifier the gain was the same but there was no phase shift. for the push-pull amplifier the gain was 2900 for the calculated values and 2k for the simulation, the gain was so high that it rail from GND to VDD, in order to fix this we had to voltage divide the input with a 10k and 10 ohms resistors and the experiment gave us a 1.68k gain with a 180 degree phase difference.

Return to EE420L front page