On page 625 you state that a system with positive feedback can be stable if its closed-loop gain is less than one. How do I simulate the loop gain of

the BMR in Fig. 20.15 to see that it’s less than one?

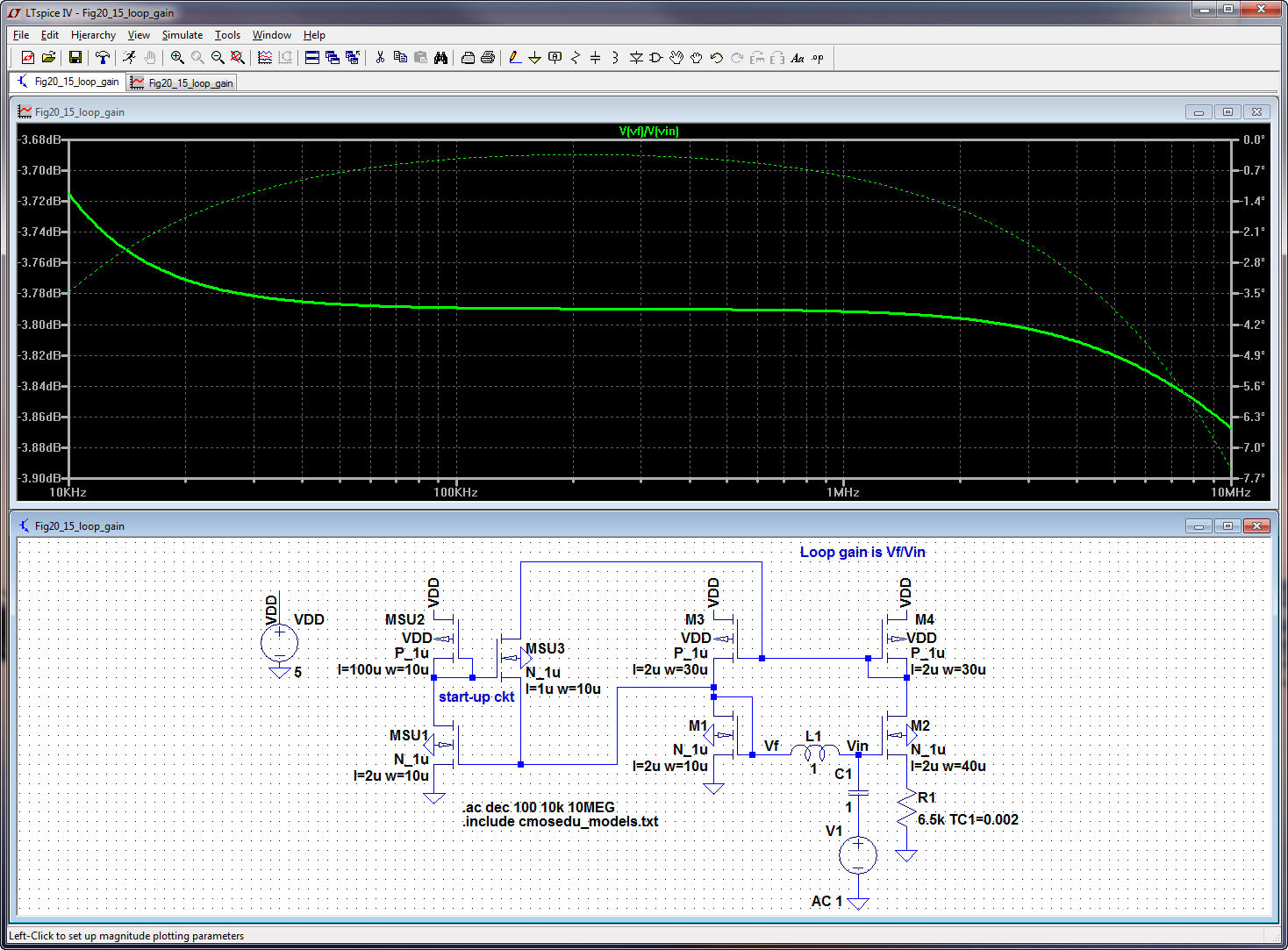
One way to simulate the loop gain, v_f /v_in or A_OLβ, is seen below (click for a larger image). The inductor is a short for DC but blocks the AC input

signal. Note the use of a huge capacitor and inductor (we can do this in a simulation ;-). For DC purposes this schematic is exactly the same as the

one seen in Fig. 20.15. See additional comments at the bottom of the page.

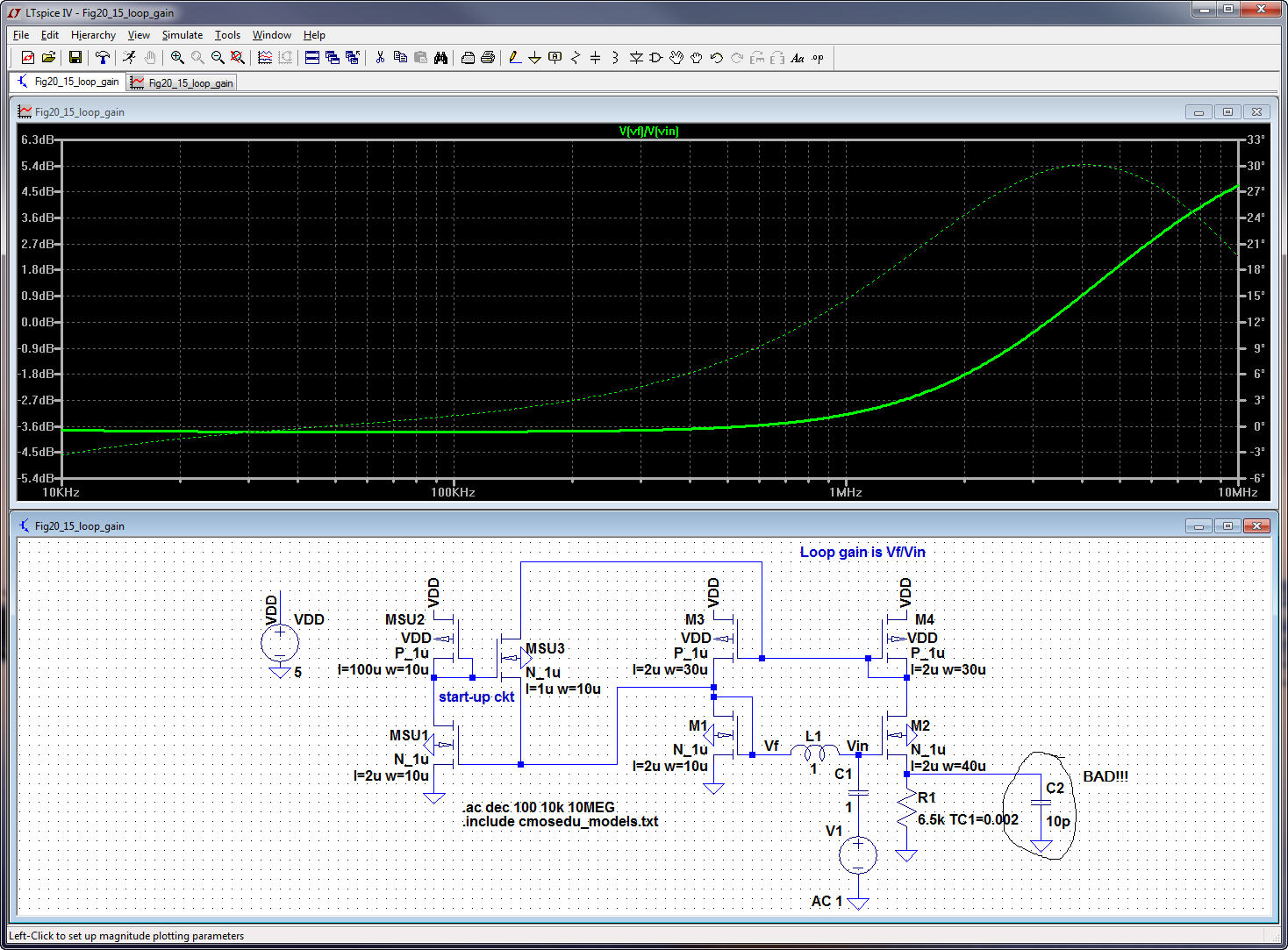
Note that, as mentioned on page 625, it’s easy to increase the loop gain by increasing the capacitance on M2’s source to ground (this is bad!, see below).

A few more comments (for the analog gurus ;-), there are many ways to look at this circuit. Here is one. The output is the drain voltage of M2, v_d2. Since the

V_SG of M4 is set by this output voltage we could also say that the output is the drain current of M4 or M2. The open circuit gain, A_OL, is v_d2/v_in which is

(1/g_m4)/(R1 + 1/g_m2) noting that this is less than one. Also note that g_m3 = g_m4 and g_m2 = Kg_m1 where, above, K is 4. The feedback voltage, v_f, is connected

directly to the input (no external source, that is, it’s self-biased) and given by g_m4v_d2/g_m1. So we can write β = g_m4/g_m1 which is often close to one. The loop

gain is βA_OL which is simply A_OL (the open-loop gain) when β = 1 (which is the case above). Since the circuit employs positive feedback we can write the

closed-loop gain as A_CL = A_OL/(1 – A_OLβ). So, as can be seen here, if A_OLβ is greater than or equal to one the circuit becomes unstable. A good design will

ensure that the loop gain, A_OLβ, is well below one.

Again, repeating the above information, we can increase the loop gain by shunting R1 with a capacitor. This drives the impedance at the source of M2 towards

ground with increasing frequency, this is bad!

Note that we are using an AC analysis when discussing stability. A DC analysis is used to determine operating point.

Also note that it’s more correct, in the last paragraph on page 625, to use “loop gain” instead of “closed loop gain” since a loop gain, A_OLβ, of 0.6 will

result in a closed loop gain, A_CL, of 1.5 (which obvious isn’t less than 1 ;-). This typo is fixed in the third and later printings of the third edition.

Return