Lab

Lab 2 - ECE 421L

Authored by Batya Vishnepolsky, vishnepo@unlv.nevada.edu

9/5/23

Lab description

in this lab we learn about the design of a 10-bit digital to analog converter (DAC), and build one using n-well resistors in Cadence.

Prelab Description

In the prelab, we have to do the following:

Back up our work from the lab and the course
Read the entire lab write-up at this link
Upload the zip file and add relative definitions so it will work

Open and run the schematic of the ADC_DAC already in place and simulate it:

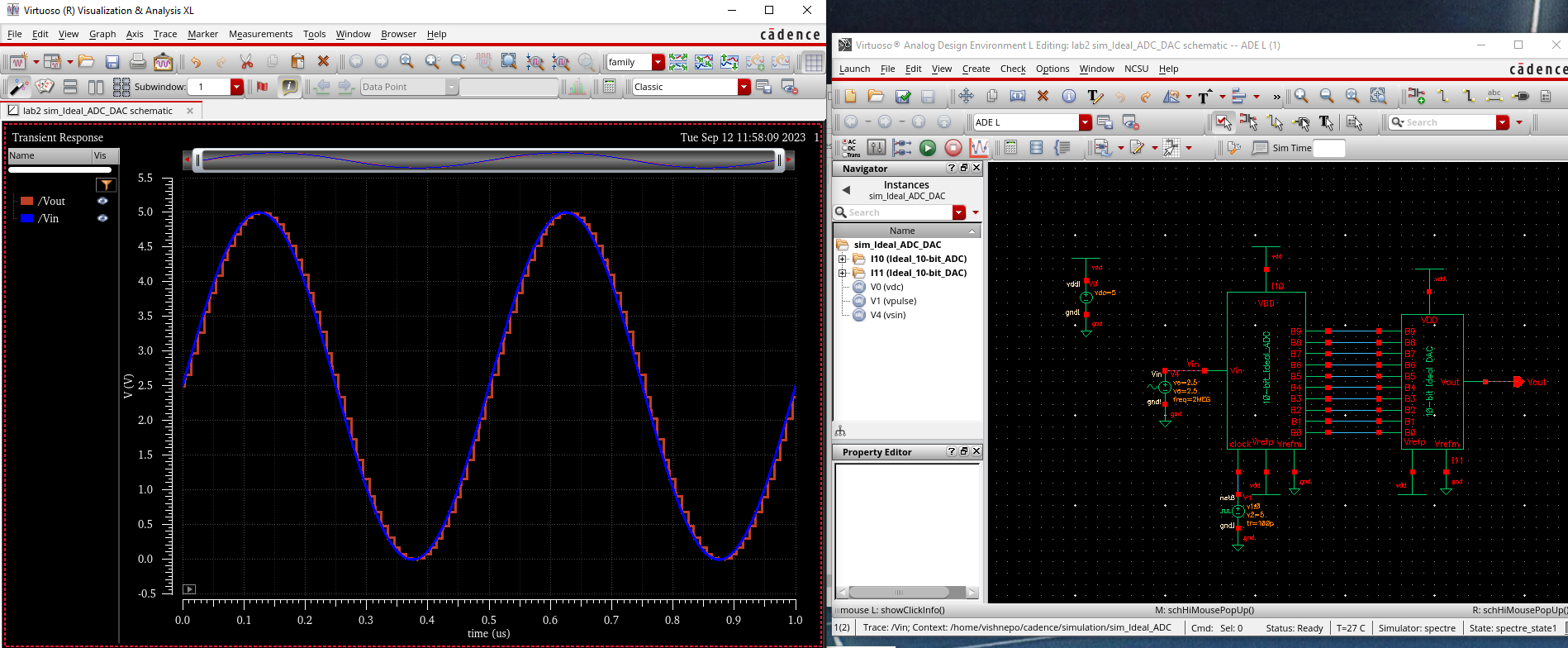
Prior to coming into the lab, understand how the input voltage Vin is related to B[9:0] and Vout

B[9:0] is a binary representation of the input signal in ten bits, from 0 - 9. What comes out of the ADC is a binary representation, and then the bits are inputted into the DAC, which will determine the Vout amplitude based on the binary input. The larger the input signal Vin is, the larger the binary representation willbe. And consequently, the more bits that are high, the larger the final output Vout will be.
Vout is outputted in what looks like "steps". This is beacuse the bits are turn on or off depending on if the input signal is a certain voltage or not. Only onse the voltage passes a certain threshold, will the bit turn on. This is why we see steps, these steps represent the threshold that is needed for the next binary value to go up. The minimum step needed to recognize a voltage increase is the least significant bit (LSB). We calculate the LSB by using the equation Reference Voltage/ 2^N bits. In the case of a 10 bit ADC, the LSB value is ~4.88mV.

In order to better understand the above, I observed what would happen when my input voltage was 2.5mV. This outputted a much simpler graph to look at, I was able to observe that the LSB was indead 4.88mV, as it the square input would only turned on and off at that value.
Last, I backed up all my work and saved it.

Lab Work:

Tasks that I need to accomplish from the lab page are:

Design of a 10bit DAC using 10k R nwell resistors
Determination of output resistance of the DAC
The delay
Symbol for my design
Simulations to verify all of the above

Designing the 10-bit DAC using N-well Resistors that are 10k:
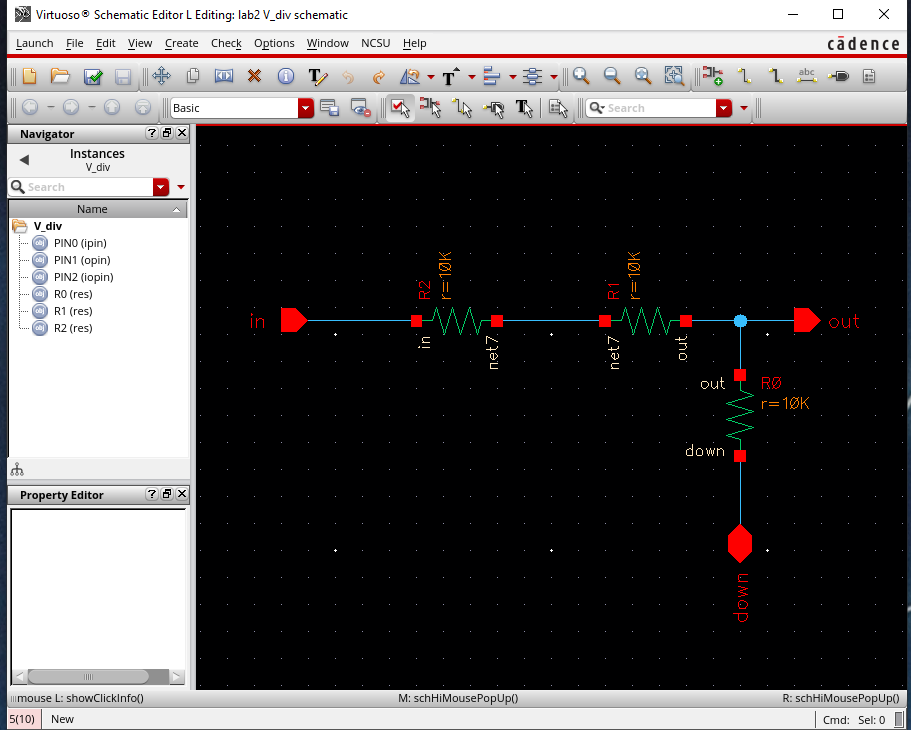
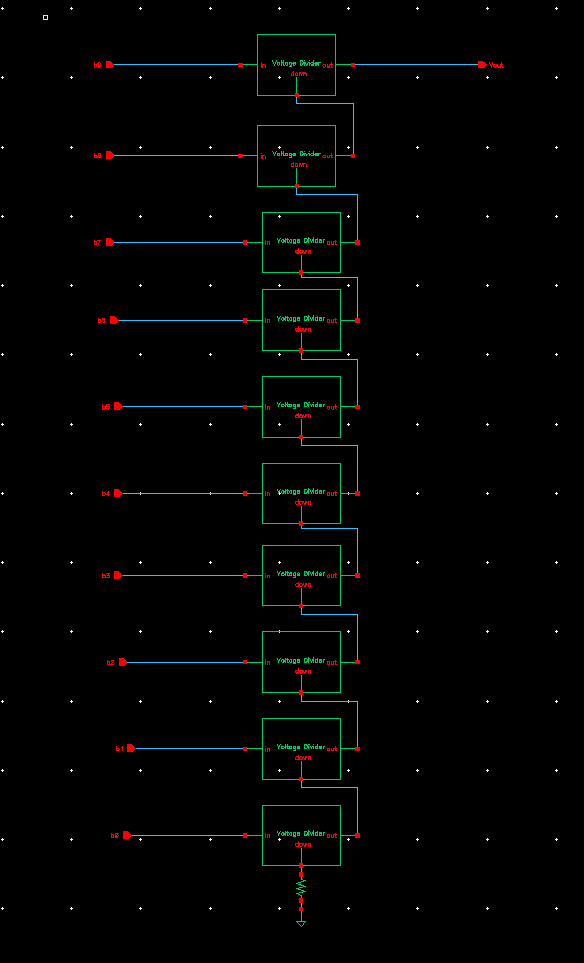
You can create a simple voltage divider for a DAC purposes by having three resistors of the same value (in our case 10k), and having the output, Vout occur between the 2nd and third resistor.

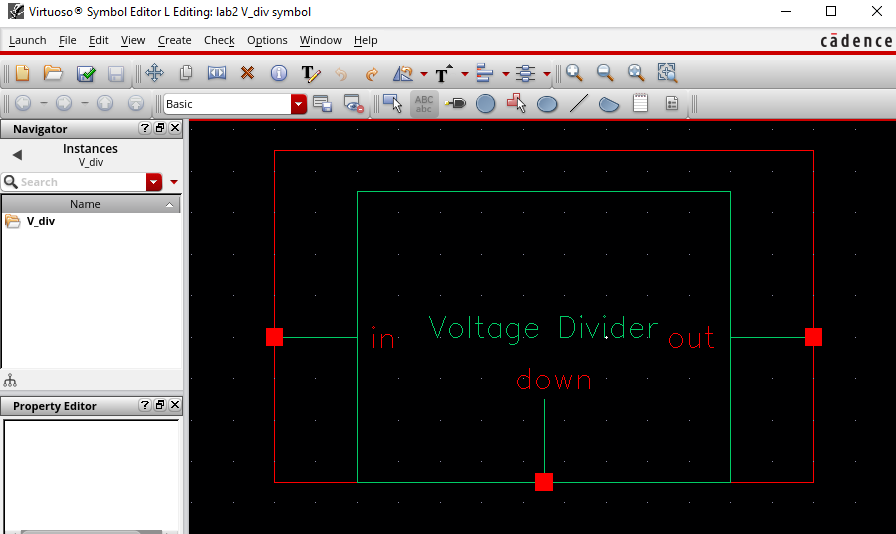
Additionally, I created a symbol for the voltage divider:

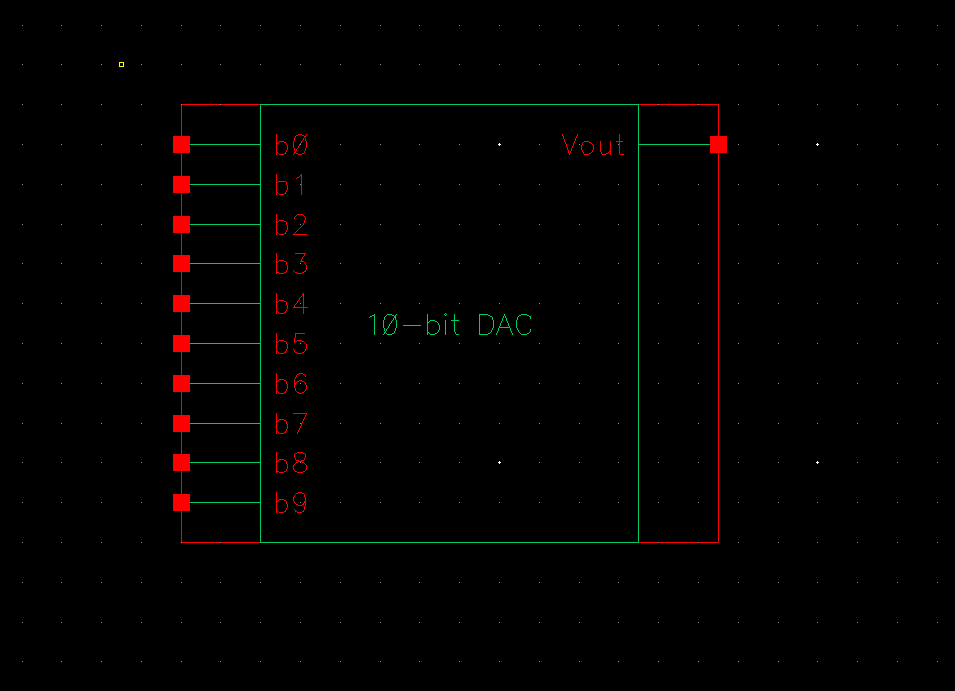
I then combined 10 voltage dividers together so that I can make a 10-bit DAC. This is what it looked like, and I also made a symbol.

Determination of output resistance of the DAC

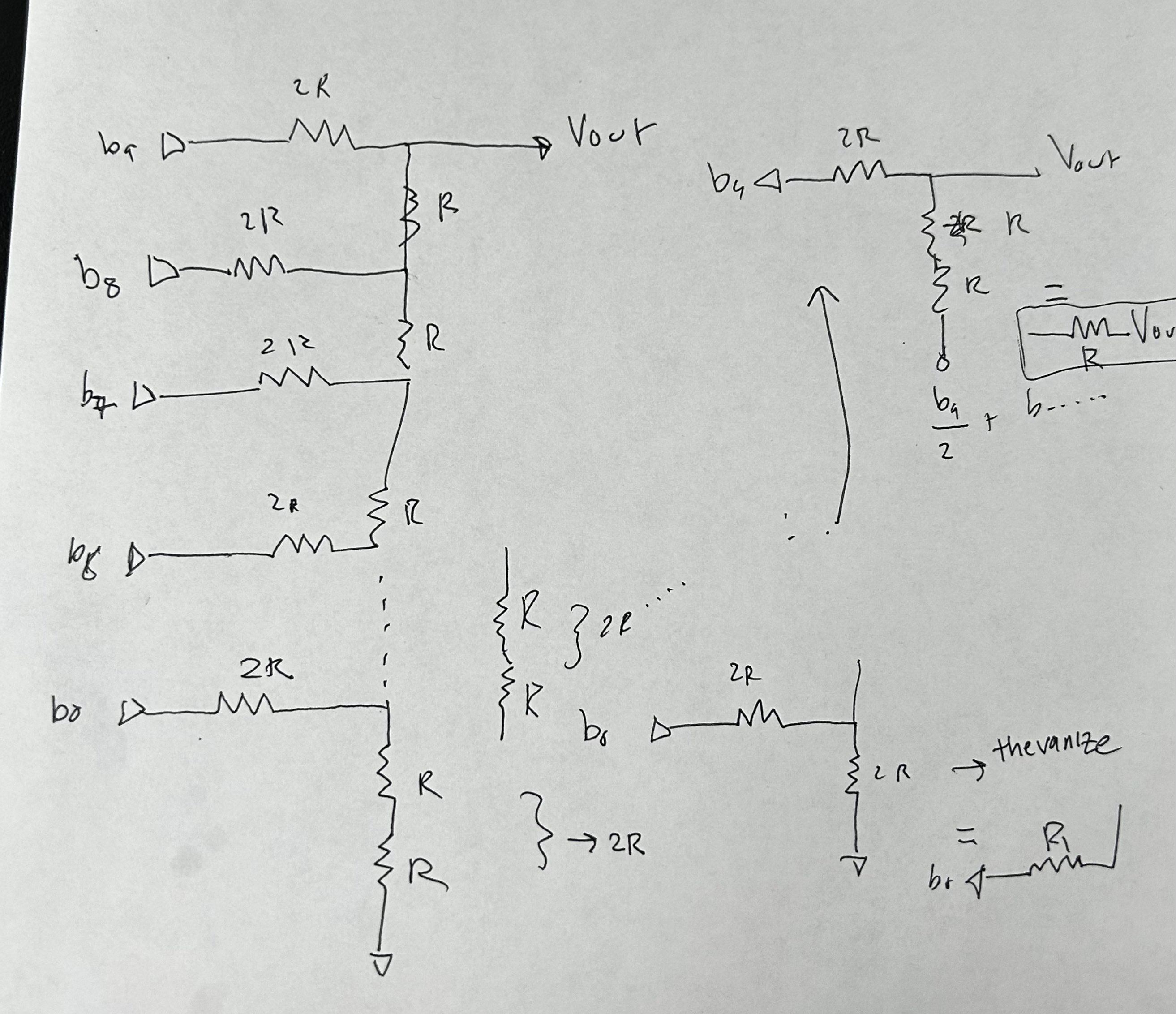
In order to determine the output resistance I drew the circuitry of the voltage dividers attached to each other. I combined the two resistors in series with each other to produce 2r, then I thevanized the 2r with the 2r to create r. This process repeated until I was at the top of the circuit. This resulted in an overall voltage of just R, and in this case the resistance R = 10k. (This is shown in the picture below).

Delay with Capactive load on the DAC:

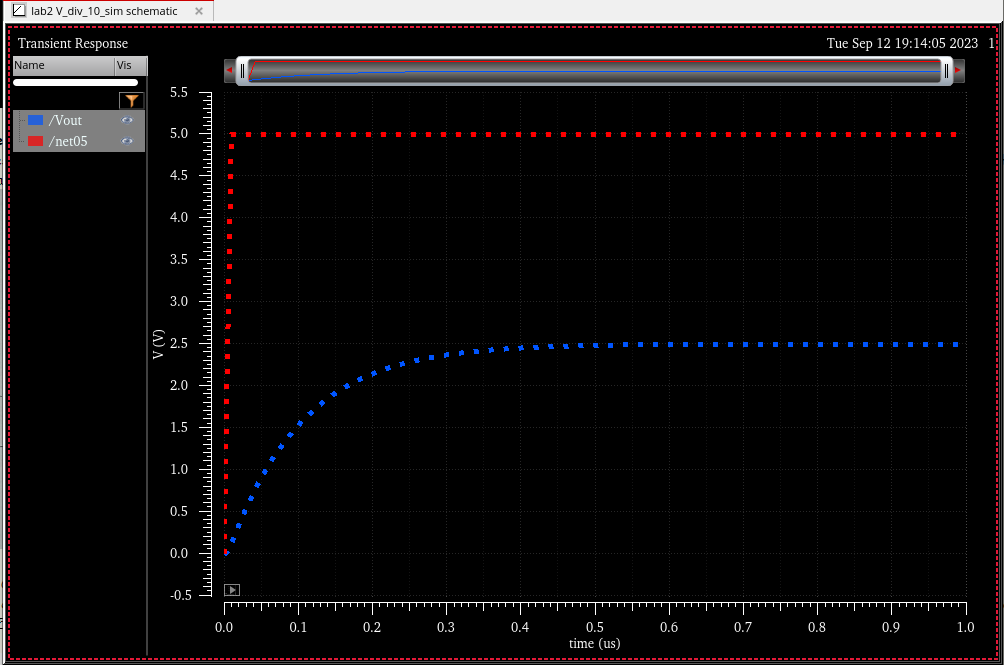
When grounding all the bits to zero except for B9, the circuitry gets reduced to a typical RC circuit, meaning that the time delay should be .7RC = .7*10k*10p. (I chopse 10pF as my capacitance on a whim, you can choose any value). When calculating this, we get 70ns, which as seen in the simulation, when we reach 1.25 (half of the maximum), we have about 74 nanoseconds, which is similar to our calculated result.

Simulations with the ideal ADC to show my design actually works!

Schematic connecting the ADC to the DAC (no load):

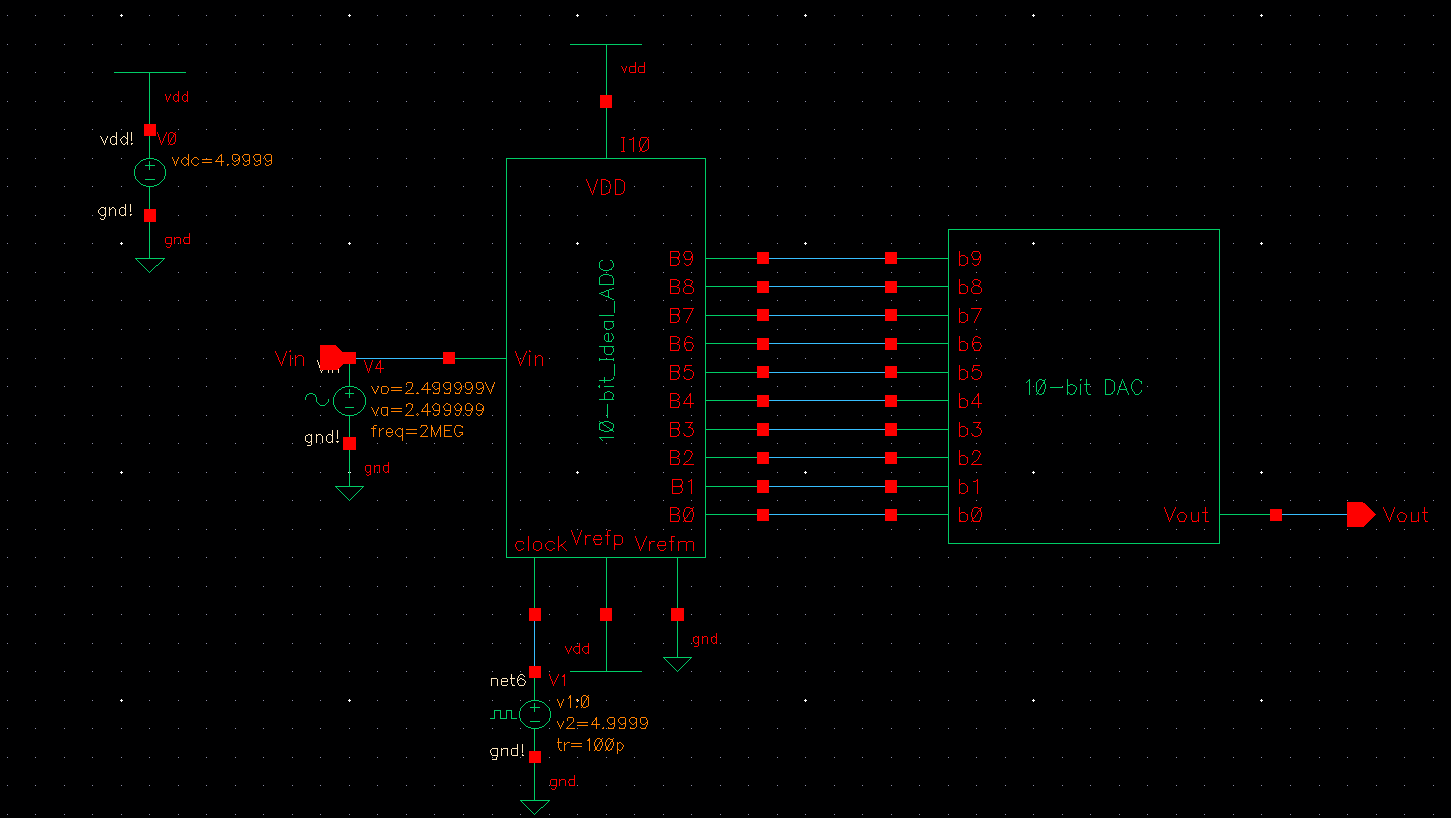
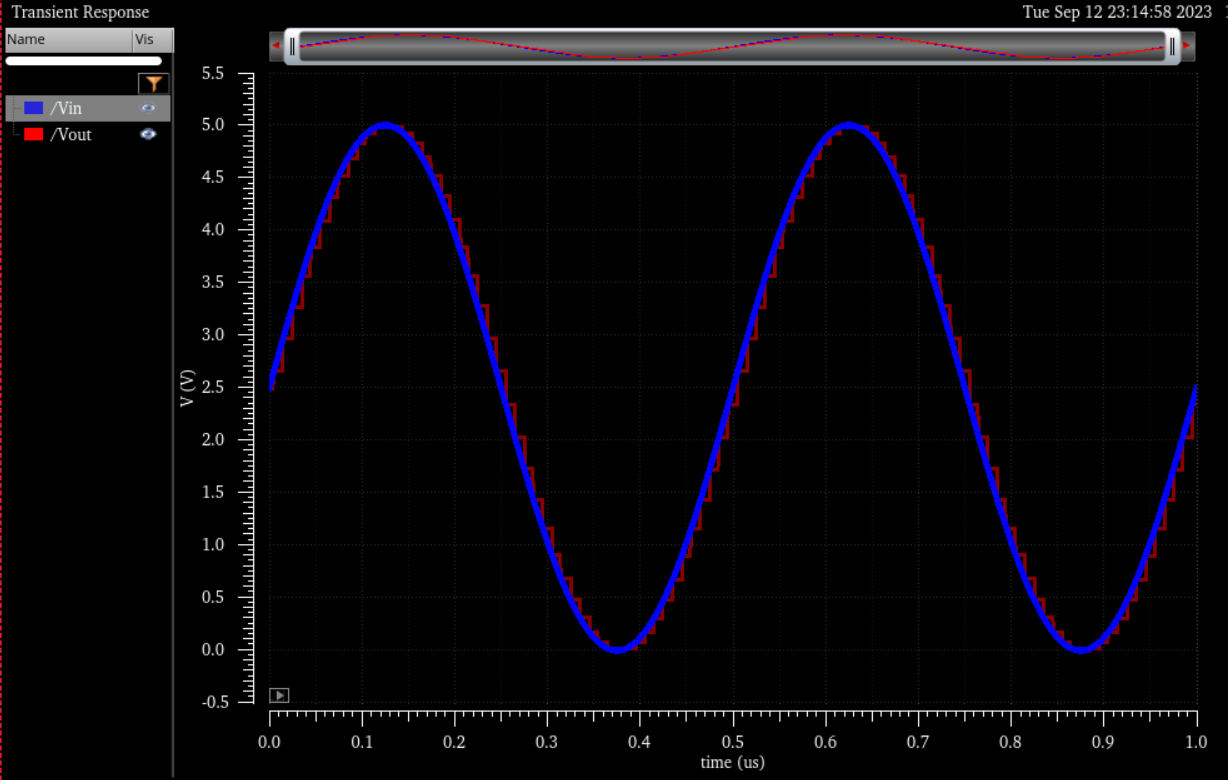
Simulation results:

We get the same result as the original ADC_DAC connector:

Schematic with resistive load

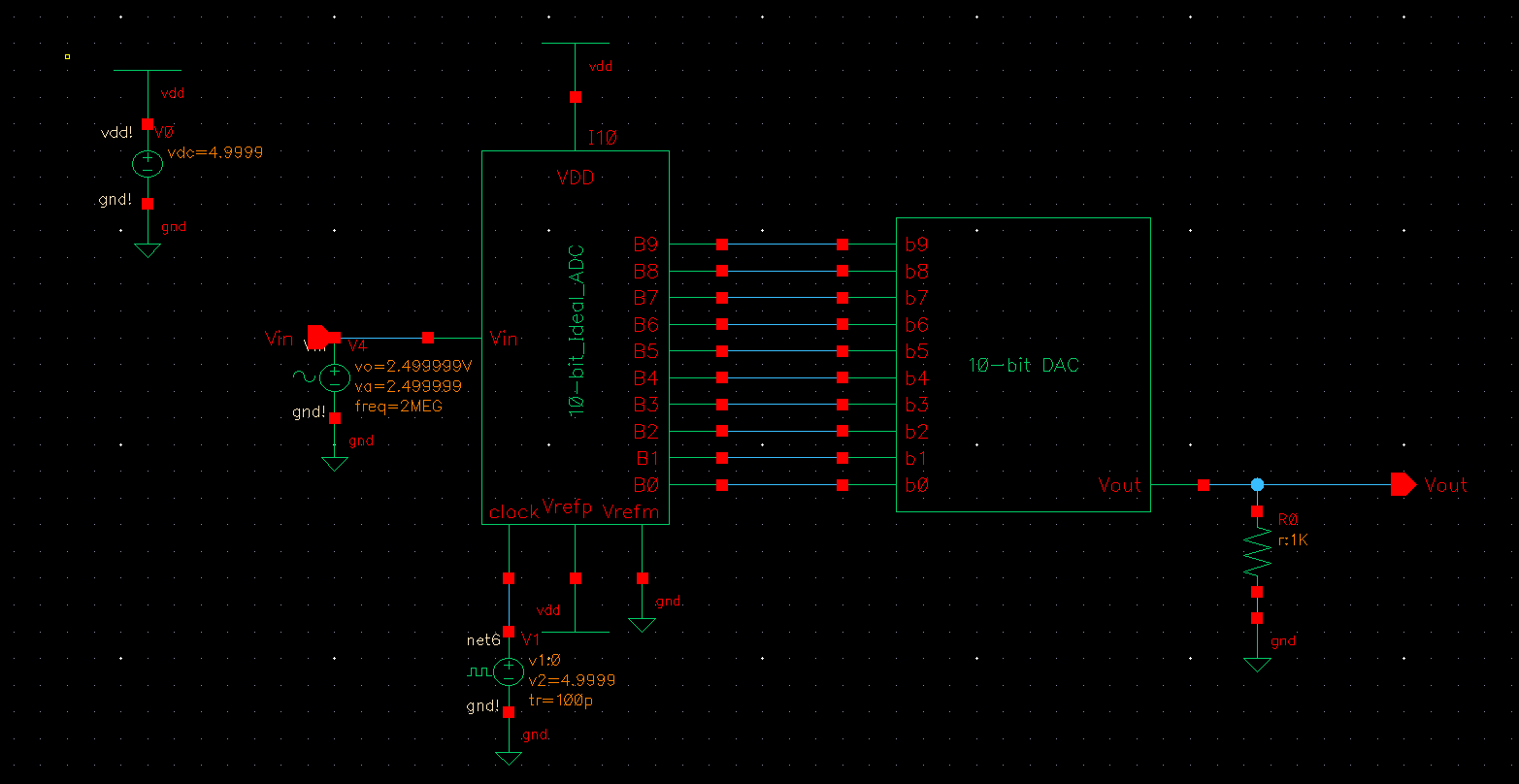
Simulation results:

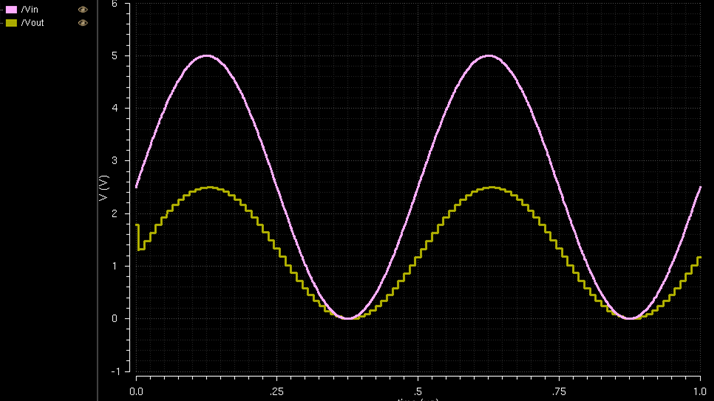
Having the resistave load clearly shrinks the output by a factor of half. This is because we will get a voltage divider circuit where the result is a 10k resistor and a 10k resistor in series, with the output between them. This effectivly cuts the circuit into two.

Schematic with capacitive load

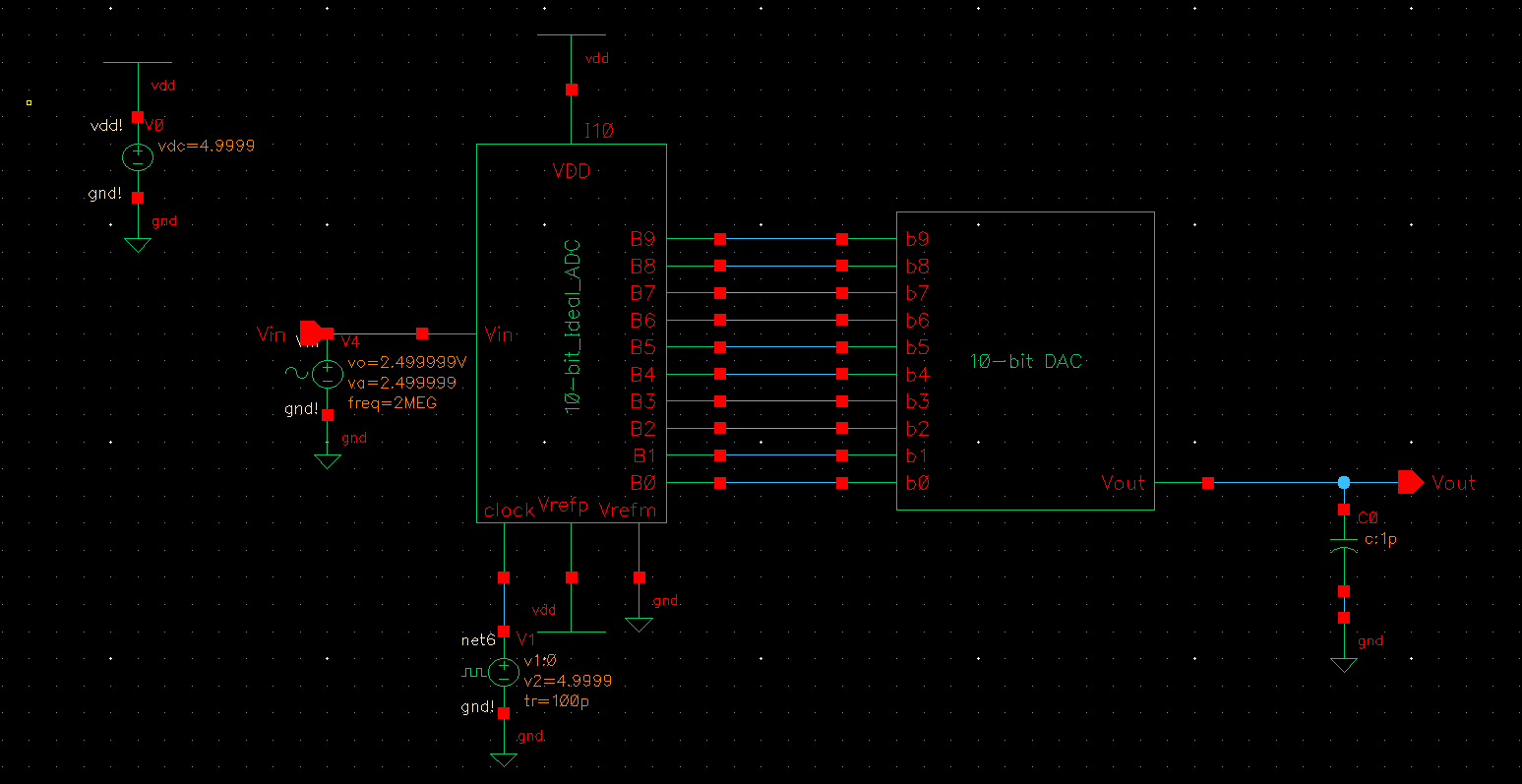
Simulation results:

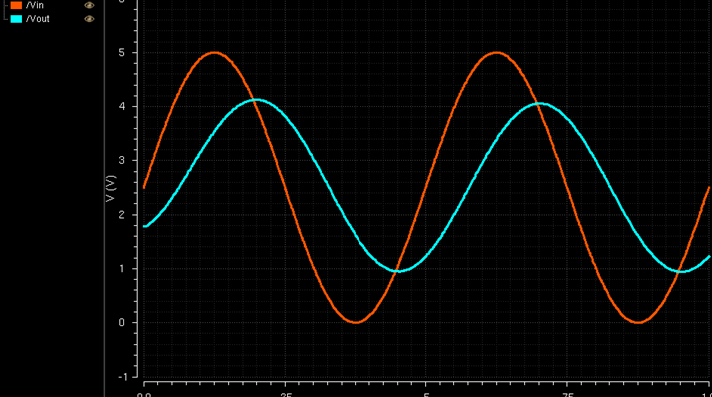
The added capacitor smooths out the result, and the magnitude is closer to the top becaue the resistor from previous simulation is now gone. However, the capacitive load also causes a slight DC offset as well. The input now lags as well.

Schematic with R/C load:

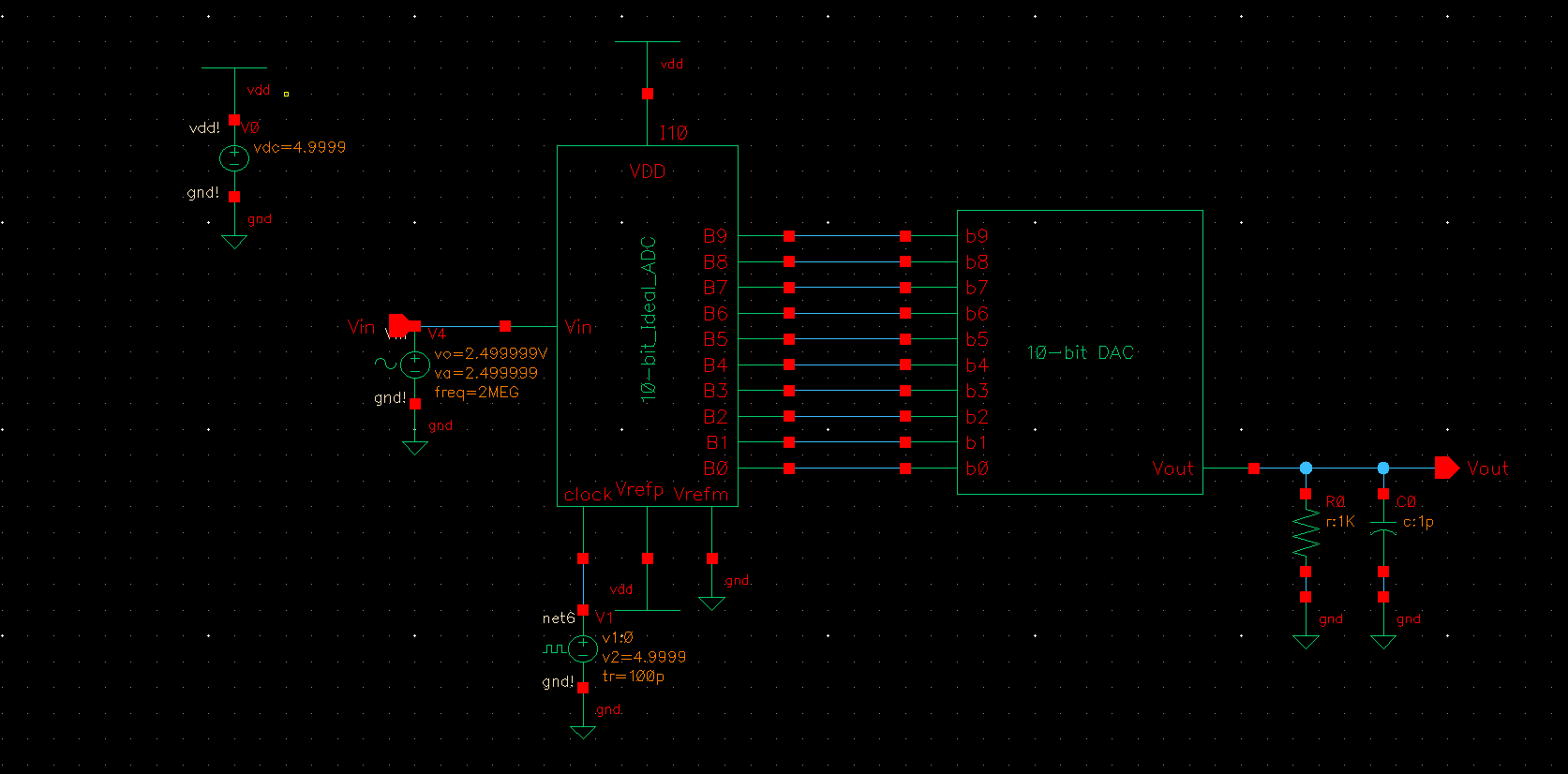
Simulation results:

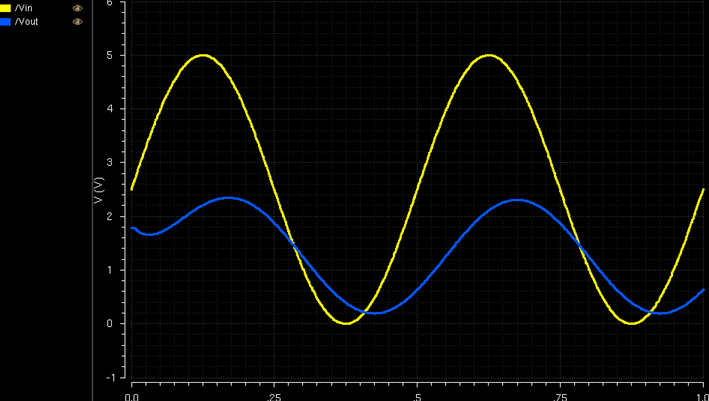
Over here, the capacitor smooths the output, and the resistor shrinks the magnitude, this gives us a halved amplitude as well as a smoothed and delayed curve.

As an overall conclusion, it is safe to say that there is no lagging for the output when there is no capacitor present, however adding a capacitors smooths the responce which the engineer desigining the DAC might want to implement because otherwise, the output will be a jaggedy binary representation of an analog signal.

In a real circuit that is implemented, if the switch resistance is not small when comparing to R, then the overall equivilant resistance would not be equal to R and the output will be messed up. In order to fix this, the resistance of the DAC should be recalculated to match the load resistance in order to ensure the output is closest to the value the user needs.

I did have problems with my simulation convergence, so I forced the simulation to convergae by changing parameters in Cadence as advised in the lab 2 instructions.

I backed up all my lab work as well, and emailed it to myself throughout the duration of this lab.

Return to all of Batya's Labs