Lab 7 - EE 421L 

Authored by Josh Jensen

jensej3@unlv.nevada.edu

10/25/23

  

Lab 7: Using buses and arrays in the design of word inverters, muxes, and high-speed adders

   

Prelab: Go through Tutorial 5

   

This tutorial walked through the steps of building a ring oscillator schematic, symbol, and layout
from basic components (such as the inverter).
   

Schematic:

    

prelab_ring_osc_schematic.png

   

Symbol:

    

prelab_ring_osc_symbol.png

   

Layout: (click for a larger picture)

   

prelab_ring_osc_layout_small.png

   

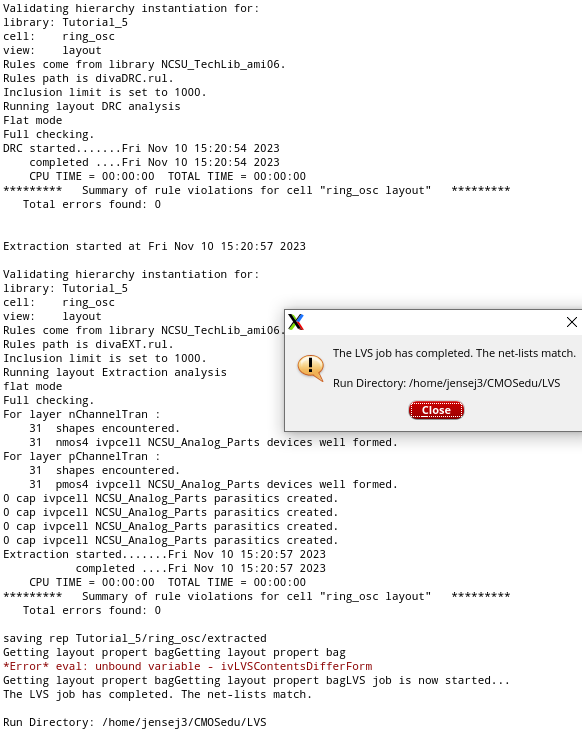
Last but not least, the design rule verification:

    

prelab_ring_osc_checks.png

   

Lab:

   

First, I followed the outlined process of simulating the 4-bit inverter array.

   
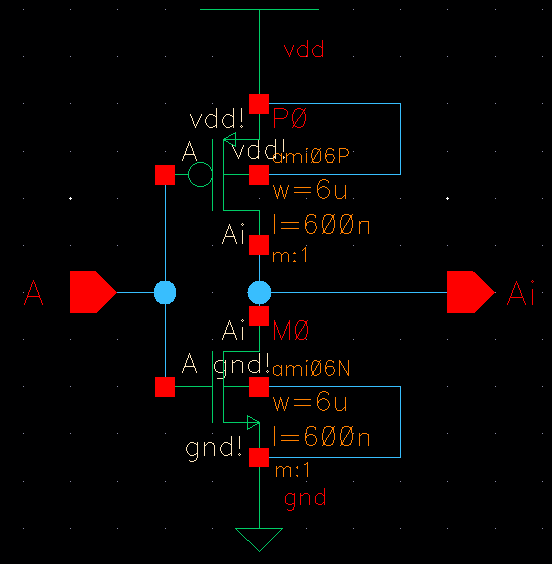
Inverter schematic:
    
inv_schematic.png

   

4-bit inverter array, using the inverter symbol:

   

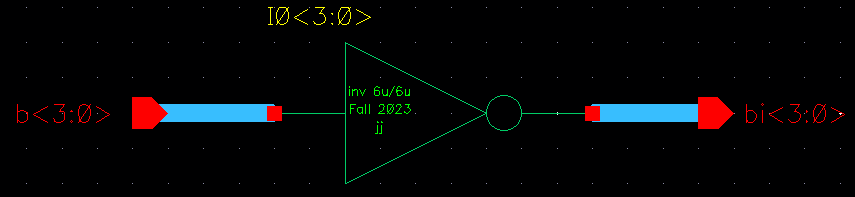
inv4_schematic.png

   

Simulation schematic for the 4-bit inverter array:

   

sim_inv4_schematic.png

   

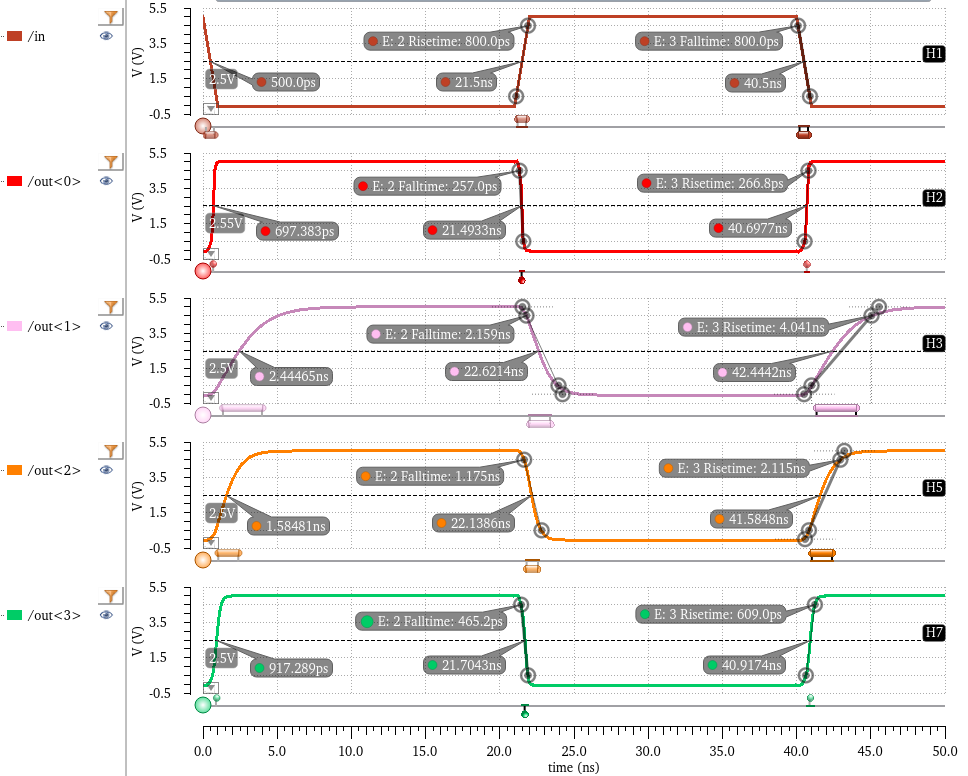
Results for this simulation:

   

The effects of the capacitive loads are seen in the delays as well as the rise and fall times of the signals.

   

*For the following measurements, I used a 10%-90% definition for rise and fall times.

   

We see that without any capacitor, out<0> has barely any delay, and in the middle of this section even appears to cross the 2.5V

midpoint before the input signal (21.4956ns vs 21.5ns). The rise/fall times are also rather small at less than 50ps each. However,

the fall time is noted to be about half that of the rise time. This is because the transistors used are all 6u/0.6u, so the PMOSes

have less resistance (by about half) than the NMOSes. As rise time is proportional to the PMOS resistance and fall time is

proportional to the NMOS resistance, this leads to the rise time being about half of the fall time. This general trend will continue

for the rest of the inverter signals and probably for the rest of the lab as well, because the transistors will remain the same size.

   

This doubling can also be seen in the delays for rising signals vs falling signals, for the same reason.

   

Comparing this to the out<3> signal, which runs through a relatively weak 100fF capacitor, we see increased delays of about 400ns

(rise) and 200 ns (fall), as well as increased rise times (about 600ps) and fall times (about 470ps).

   

Now looking at the heaviest capacitor in this simulation, out<1> has to run through a much larger 1pF capcitor. This is reflected in

delays of 1.1ns (rise) and 1.9ns (fall) as well as edge transitiions of 4ns (rise) and 2.2ns (fall), which are again much larger than those

of out<3> or out<0>.

   

sim_inv4_plot_2.png

   

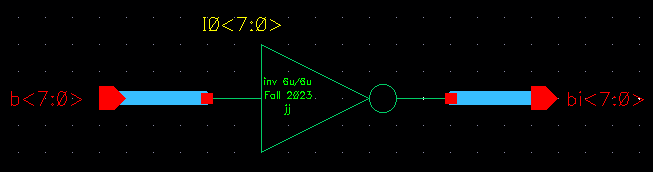
Next, I moved on to making 8-bit versions of NOT, NAND, NOR, AND, and OR gates.

   

8-bit inverter schematic:

   

inv8_schematic.png
   
1-bit NAND gate schematic:
   
nand2_schematic.png
   
8-bit NAND schematic, using the 1-bit NAND symbol:
   
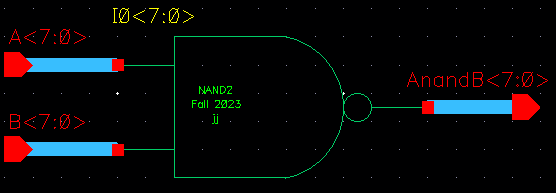
nand2x8_schematic.png
   
1-bit NOR schematic:
   
nor2_schematic.png
   
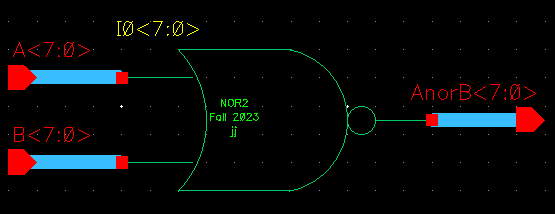
8-bit NOR schematic, using the 1-bit NOR symbol:
   
nor2x8_schematic.png
   
To make the AND and OR gates, I simplified my work by reusing the NAND, NOR, and NOT symbols.
   
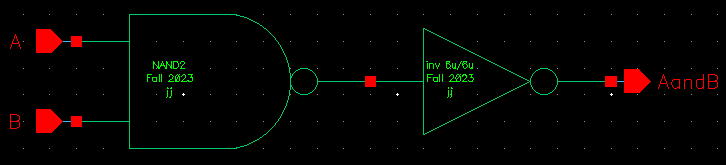
1-bit AND schematic, using the NAND and NOT symbols:
   
and2_schematic.png
   
8-bit AND schematic, using the 1-bit AND symbol:
   
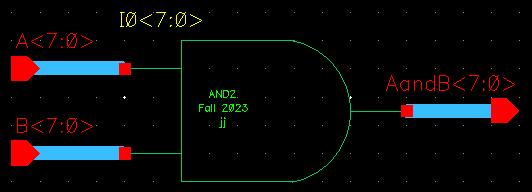
and2x8_schematic.png
   
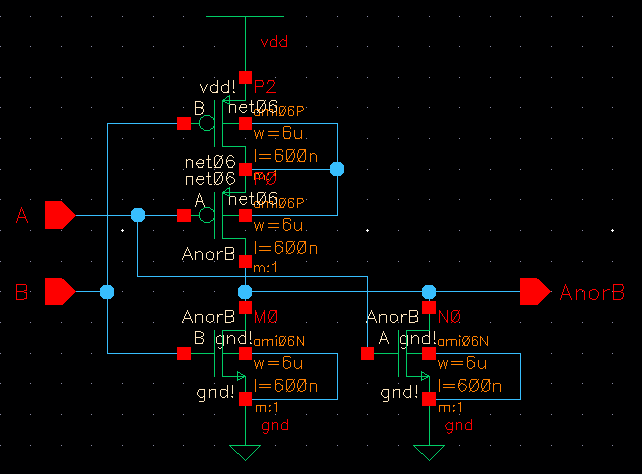
1-bit OR schematic, using the NOR and NOT symbols:
   
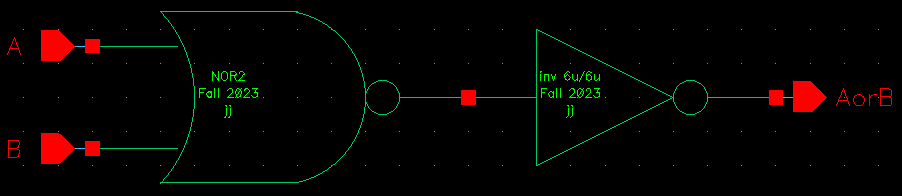
or2_schematic.png
   
8-bit OR schematic, using the 1-bit OR symbol:
   
or2x8_schematic.png
   
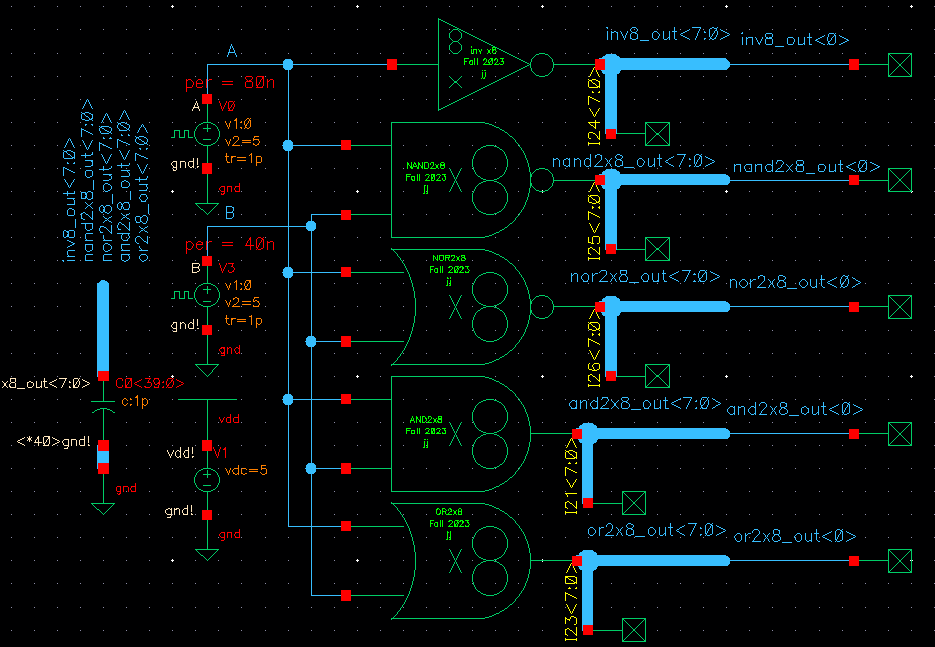
Next, I simulated the 8-bit NOT, NAND, NOR, AND, and OR gates all together.
I went ahead and used a 1p capacitor per output signal to mitigate signal spikes (it was rather extreme for the NOR gate in
particular). I only plotted one output bit from each gate since all 8 bits in each set would be the same anyway.
   
Gate simulation schematic:
   
sim_gatesx8_schematic.png
   
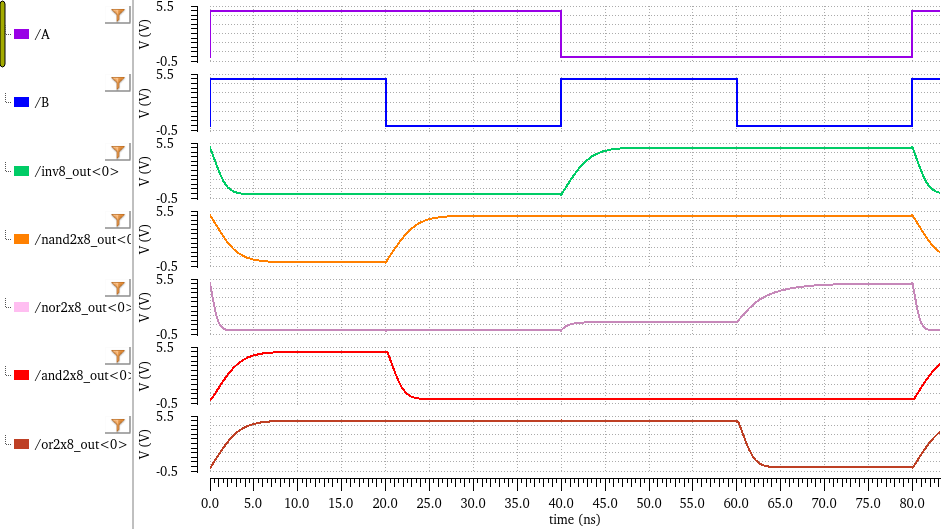
Gate simulation results:
   
sim_gatesx8_plot_2.png
   
Next, I created an 8-bit full adder using the AOI design from Figure 12.20 in the textbook. For reference...
   
Schematic: (click image for a larger version)
   
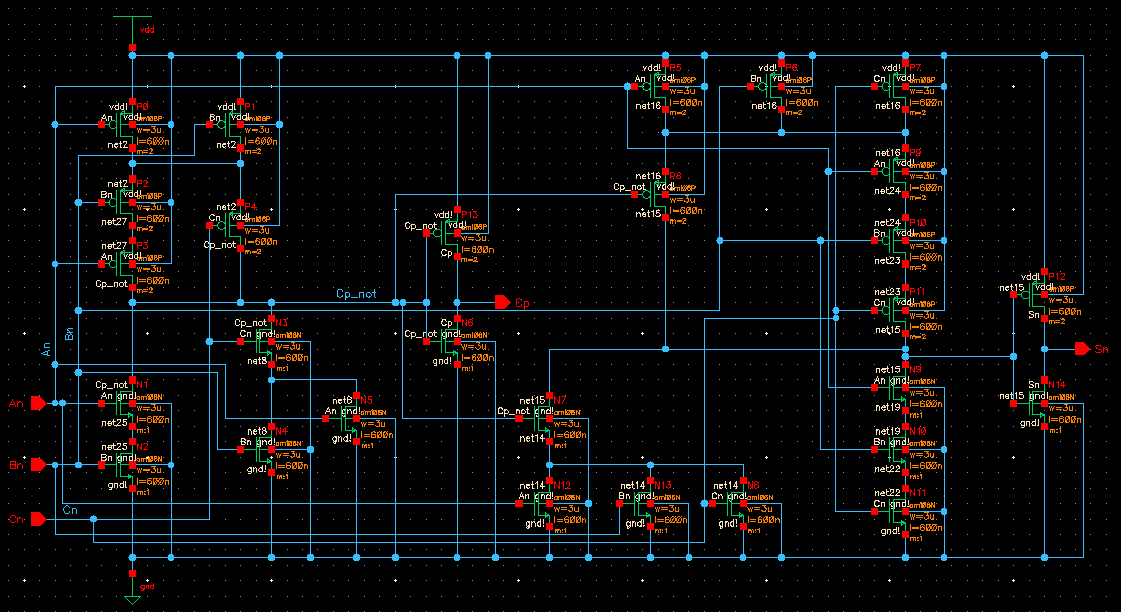
full_adder_schematic_small.png
   
As this is a new schematic I wasn't entirely familiar with, I decided to simulate it just to make sure it worked as expected.
   
Simulation schematic:
   
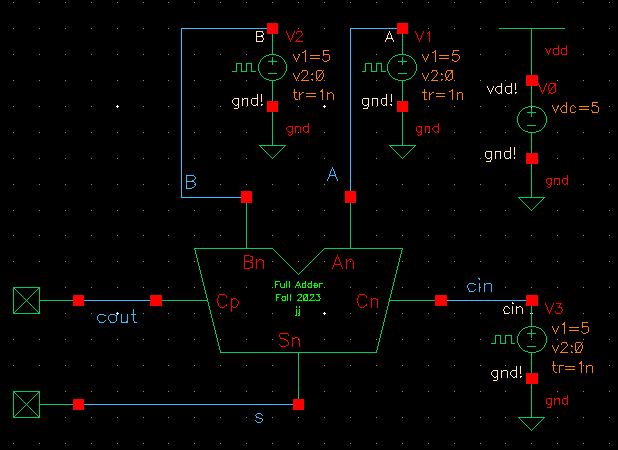
sim_full_adder_schematic.png
   
Simulation results:
Yes, this works correctly.
0+0+1 gives a carry out of 0 and a sum of 1 (01).
0+1+1 gives a carry out of 1 and a sum of 0 (10).
1+1+1 gives a carry out of 1 and a sum of 1 (11).
   
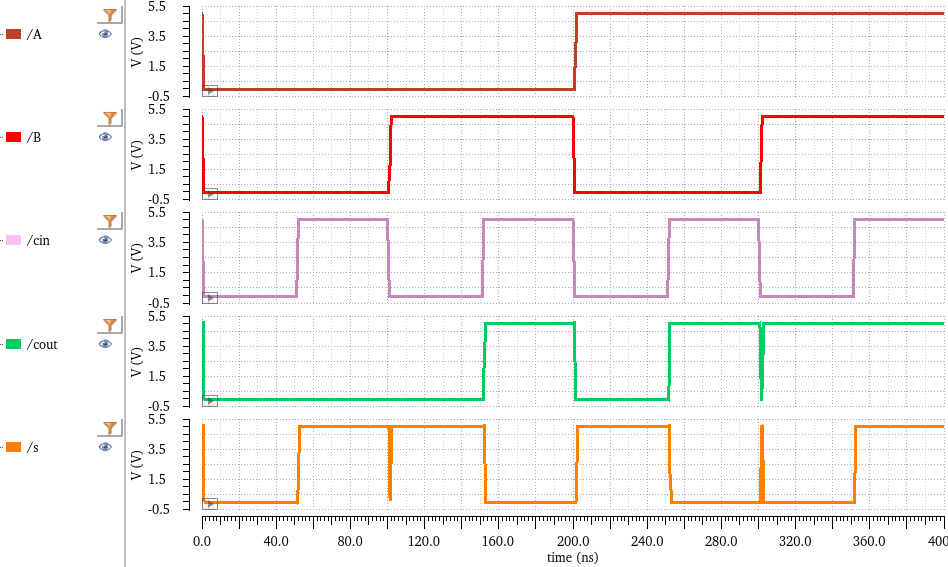
sim_full_adder_plot.png
   
After confirming that it worked, I made the layout for a single-cell full adder. The inputs and outputs are on the metal 2 layer.
   
Layout:
   
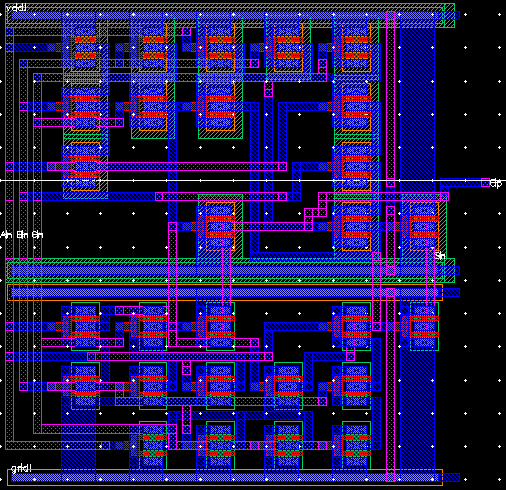
full_adder_layout_small.png
   
Next, I made an 8-bit version of the full adder.
   
Schematic:
   
I used Ci to represent the initial carry in, Cp to represent Cn+1, and Co for the final carry out.
   
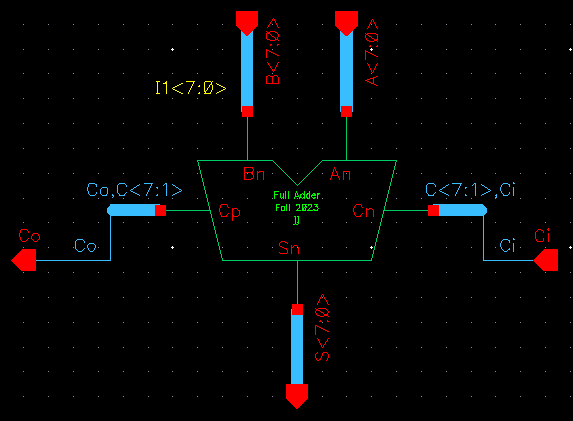
full_adderx8_schematic.png
   
Symbol:
   
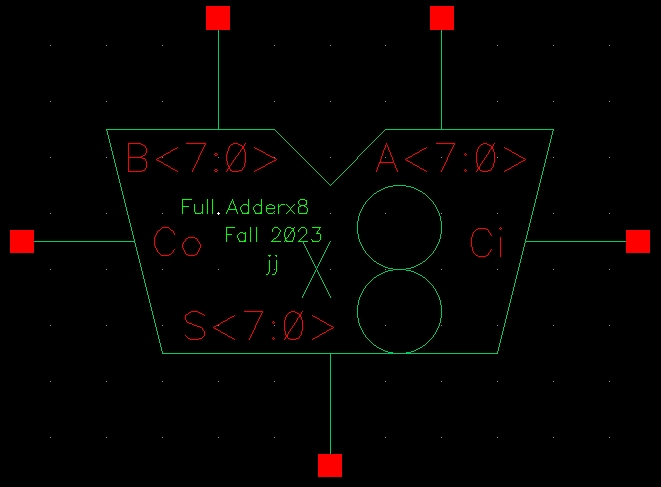
full_adderx8_symbol.png
   
Layout: (click for a larger version)
   
full_adderx8_layout_small_far.png
   
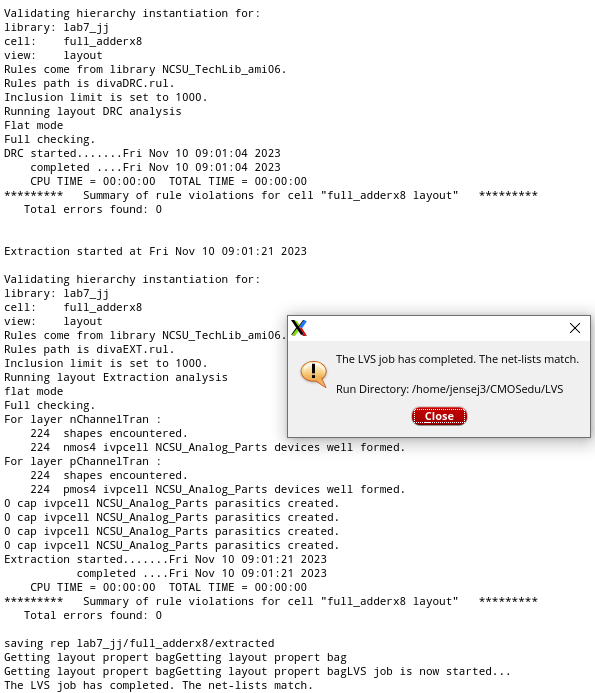
Design rule checks:
   
full_adderx8_checks.png
   
To simulate the 8-bit adder, instead of simulating all possible 2^17-1 input combinations,
I just varied A<7:4>, A<3:0>, B<7:4>, B<3:0>, and Ci as if it were any other 5-variable
logic function.
   
For example, at 36 ns, A = 1111 1111, B = 1111 0000, and Cin = 0. I would expect that the lower four bits of A would stay intact,
while the upper four bits of A and B would sum to produce 1110 and an overflow to carry out.
We see that this is what happens, as S = 1110 1111 and Cout = 1 at 36 ns.
   
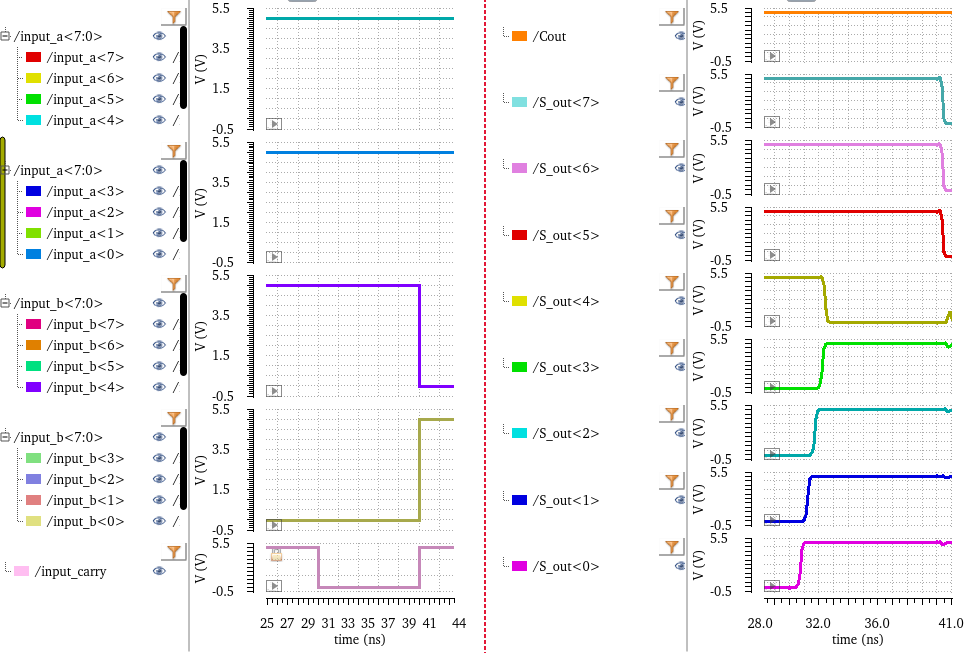
sim_full_adder_36n.png
   
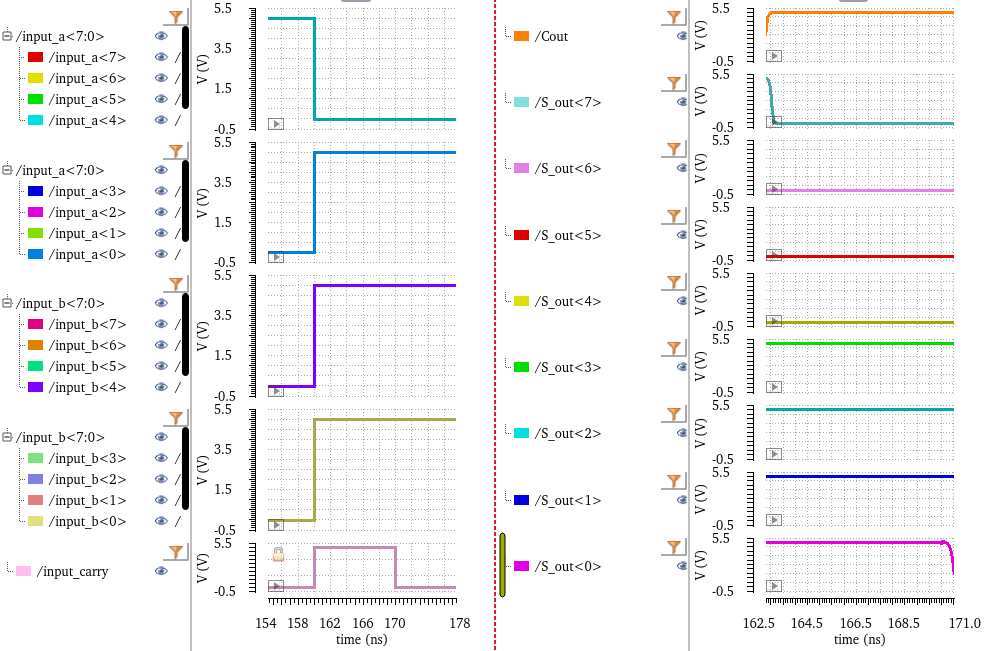
For another example, here is the plot at 166 ns. At this point, A = 0000 1111, B = 1111 1111, and Ci = 1. Performing the binary addition
by hand, I would add Ci to B, which would reset B to 0000 0000 and sending the overflow 1 to Cout. After that, A + 0000 0000 is
simply A, or 0000 1111. This is reflected in the graph, as we see S<7:4> is 0000, S<3:0> is 1111, and Cout = 1.
   
sim_full_adder_166n.png
   

   

Instruction for Lab 7

Return to list of my EE421L labs