Lab 2 – EE-421L 

Authored by Matthew Daniel McDonagh

EE-421 Fall 2021
email: mcdonm6@unlv.nevada.edu

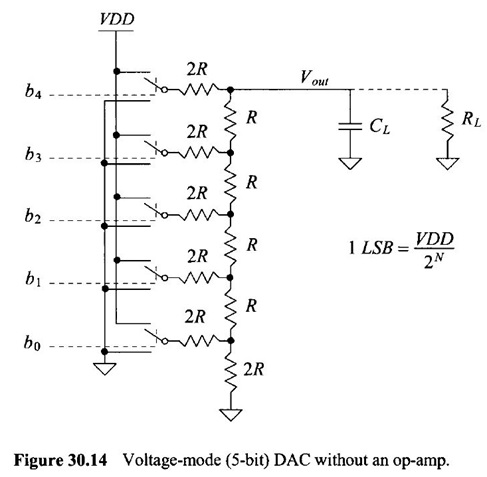
Lab description: In this lab we will be using n-well resistors to implement a 10-bit DAC. This is a laboratory introduction to digital-to-analog-converters as well as analog-to-digital converters. The design in this lab will be based upon the topology seen in the figure below, which is also in the CMOS book. CMOS technology allows multiple important implementations of these devices. The controlling input bits in the figure below are from the ADC, meaning that the inputs to the DAC are the left side of the 2R resistors. Implementation here is achieved with the R-2R ladder:

Pre-lab work:

Continuing on with tutorial 1, place all files in the proper directories using mobaXterm or terminal application of choosing. The conceptual behavior behind the converters can be elaborated on with a few short descriptions. Simple DAC are implemented with R-24 string in voltage mode. For an ADC to collect external information, analog signals must be converted to digital signals, which is completed by sampling. An analog signal can be sampled without aliasing (an effect that causes different signals to become indistinguishable). The ADC range is max input to input, its precision is the number of distinguishable inputs 2^N (where N is the number of bits). The ADC resolution is the smallest distinguishable change in input V_in.max / 2^N where a change in input causes output to change by 1. Clock speed will determine how quickly the converter can sample.

The accuracy of the sampling is computed in the following formula: 0.5 LSB / Full scale range (V_DD) = V_DD / 2^(N+1) * 1 / V_DD and the time constant associated with the DAC and the capacitive load is r = RC_L. The output formula for Vout = Vout.final(1-e^(-t/t)) the required setting time, t_setting = RC_L * ln(2^N+1) and the max clock frequency, f_clk.max = 1/t_setting.

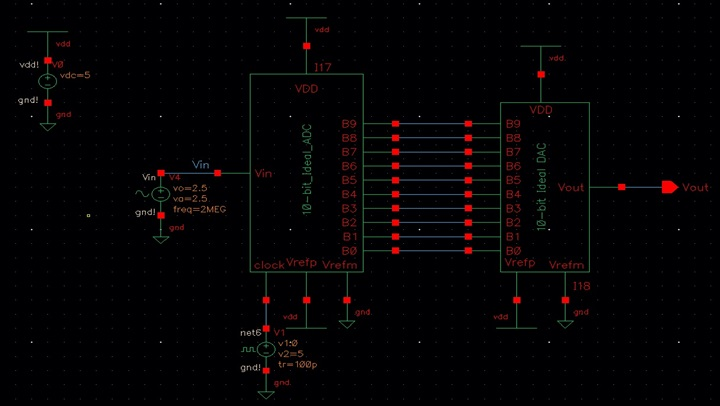
Opening the sim_Ideal_ADC_DAC schematic under cell menu:

After running a simulation (following launchàADE LàSessionàLoad stateàCellviewàOKàGreen start button (simulation of input of sin and no load):

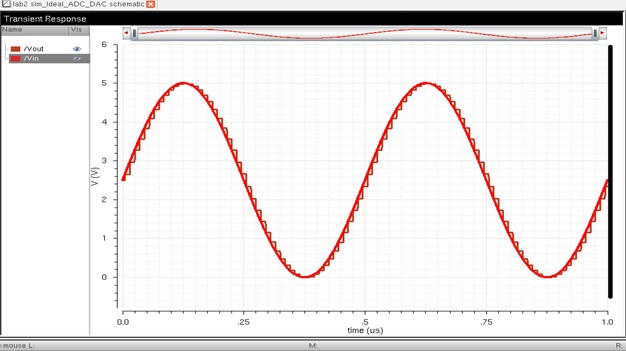
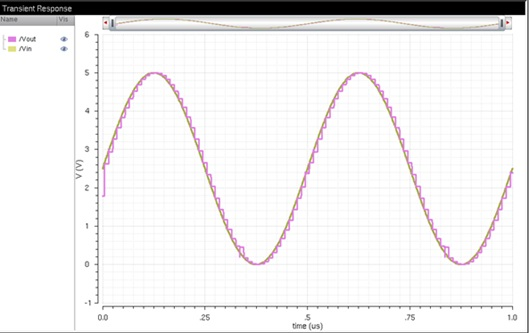
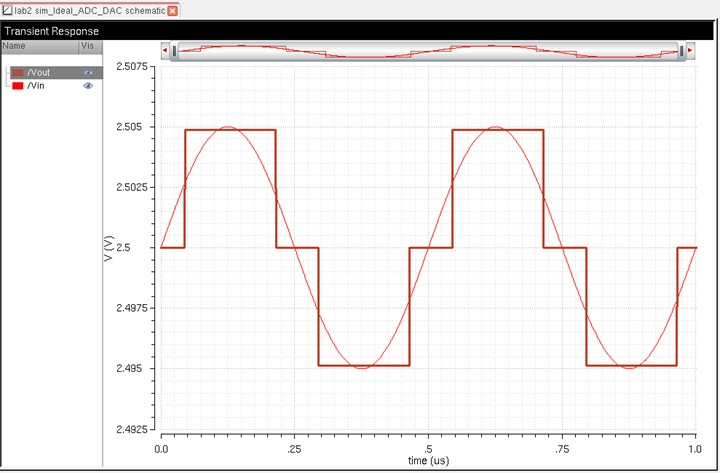
The simulation results above show the relationship between Vin and B[9:0] is that the ADC takes the input from the Vin and converts this input to a digital signal that produces a 10-bit binary value which is then received by the DAC and outputs an analog signal Vout. To discover the least significant bit (LSB) we simply use the equation shown below where we plug in our VDD and N: LSB = Vred / 2^N which delivers a value of Vout to be around 5mV. That value represents the LSB and graph below:

This concludes the pre-lab portion.

Part 1: Creating a Digital-to-Analog Converter

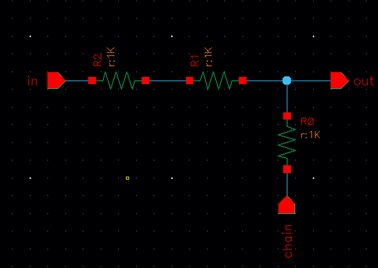
Beginning by creating a new schematic to fill in the ladder and chain the 10 together:

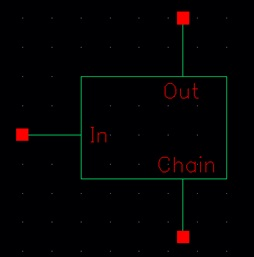
Then creating a symbol for the schematic from cellview:

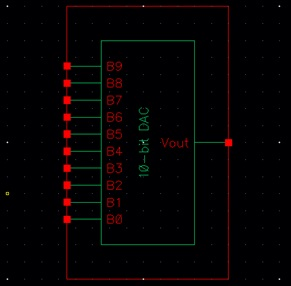
Using the symbol above to fill in a new schematic for the 10-bit DAC:

top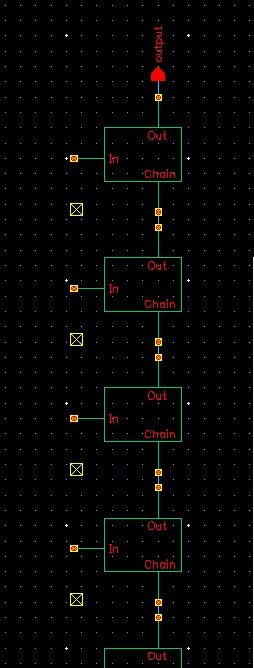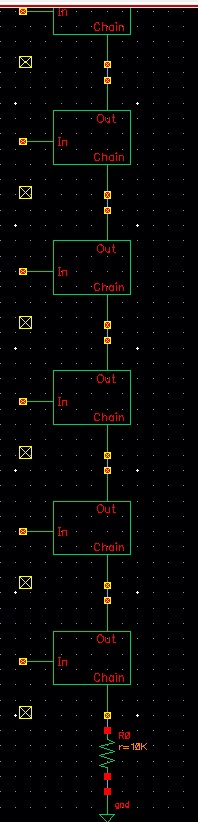bottom

To re-use the symbol which was created for the lab 2’s ideal 10-bit DAC, I copied it into the custom 10-bit DAC schematic. This is the result:

Now to calculate output resistance Rout:

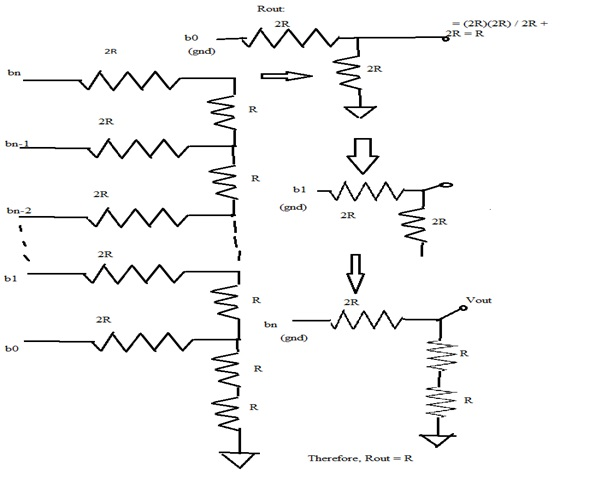
Next calculating the delay with all the pins to ground barring B9 with a capacitance of C = 10pF. The formula is: t_d = (0.7)RC à t_d = (0.7)(10k ohms)(10pF) = 70ns. The maximum output voltage for this node is determined by the following formula: Vout.max = Vin*(R/(R+R)) = ½ * Vin where Vout = ½ Vout.max. By setting 2V = Vin, at halfing that, we should see Vout.max = 1V and Vout = ½ Vout.max = 0.5V when the delay t_d = 70ns.

Here is the DAC design:

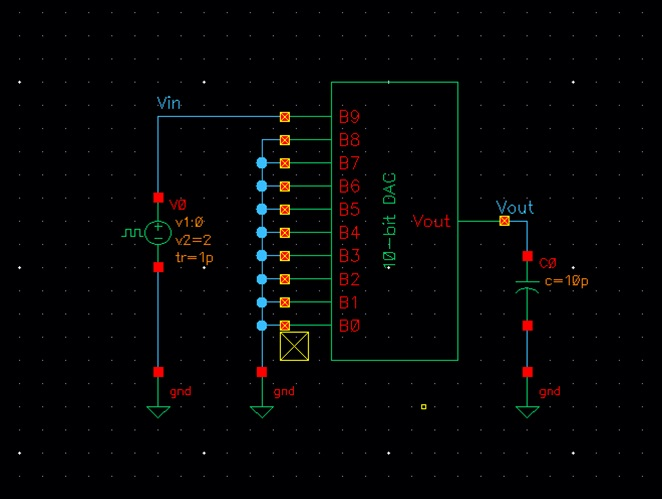
Corresponding circuit:

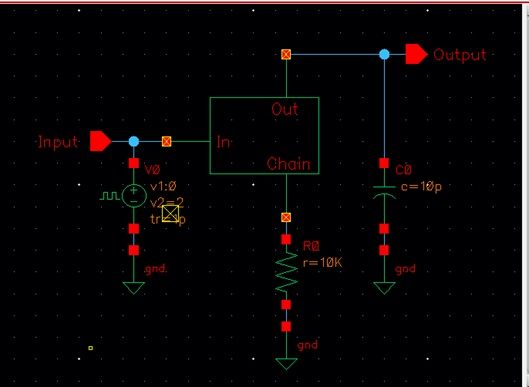
Now creating sim2_ideal_DAC and replacing the DAC component with our own:

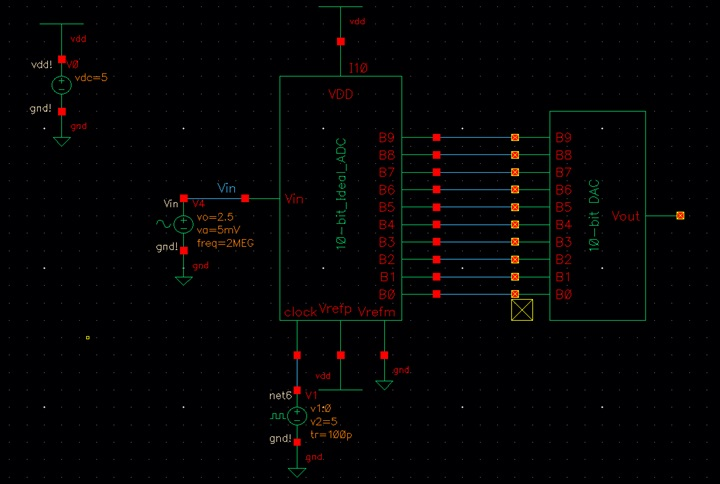
Here is the circuit under no load and its simulation result:

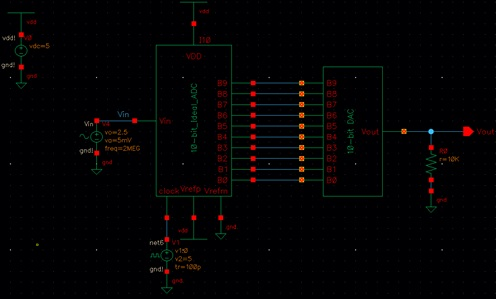
Here is the circuit under a 10k resistive load and its simulation result:

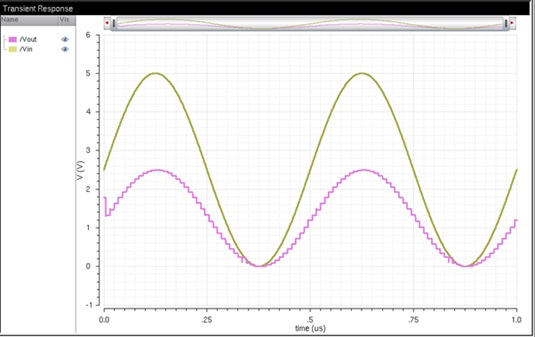
Here is the circuit under a 10pF capacitive load and its simulation result:

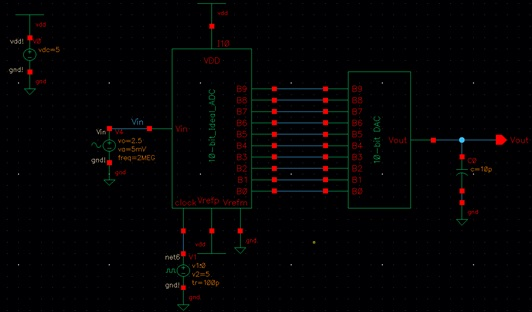
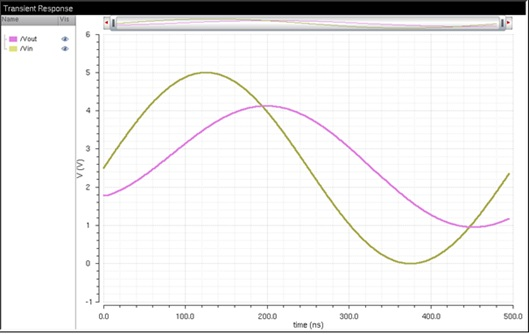
Here is the circuit under both a 10k resistive and 10pF capacitive load, and the resulting simulation:

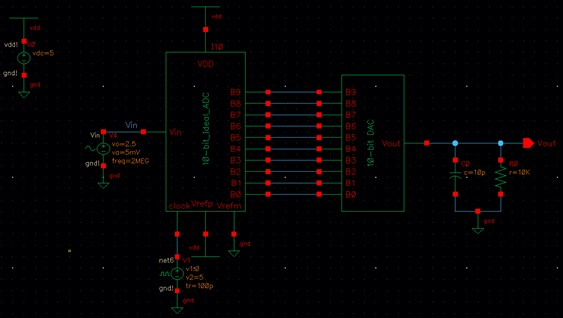
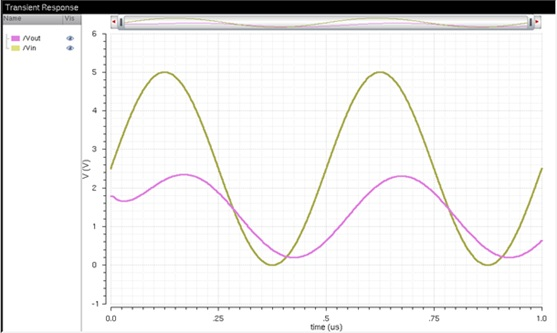
Conclusion: Compared to the value of the resistance R, if the switches are transistors or the resistance value of the switches is larger than R, there would be a different equivalent resistance of DAC. An equivalent resistance value that is larger than R would be caused by the resistances in series being higher themselves. The smaller output voltage value (Vout) would be caused by a higher resistance from the larger voltage drop across the transistor. Each new equivalent resistance value must be calculated and considered for the load of the 10-bit DAC. These simulations show that the DAC works as expected. Without a load there is simply a tiny lag, with a resistive load only the output is halved, with a capacitive load only the output resolves smoothly with a delay, and when both are present the DAC’s output experiences minimal lag and a reduced voltage value.

I will back the work up on my google drive as instructed.