Lab 6 - EE 421L 

Authored by Christopher Mikhael,

Email: Mikhaelc@unlv.nevada.edu

10/28/2014



Objective:

The objective of this lab is to become familar with the use of buses in order to use arrays for inputs. This is useful because it allows us to make test out multiple outputs easier and creates a simpler prcoess flow than duplicating components.

For this lab we will be creating 8-bit input/output arrays for: NAND, NOR, AND, inverter, and OR gates.

To create these, we must first create the schematic and for a single instance of each. We will then create another schematic that will use that instance but will include an input and output bus of 8 bits. This process is shown below for the NAND, NOR, AND, inverter, and OR gates.


NAME
 Schematic
 Symbol
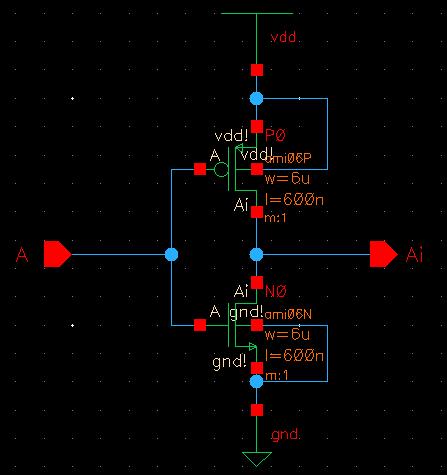
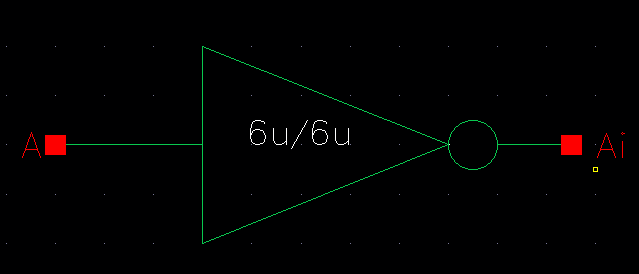
Inverter

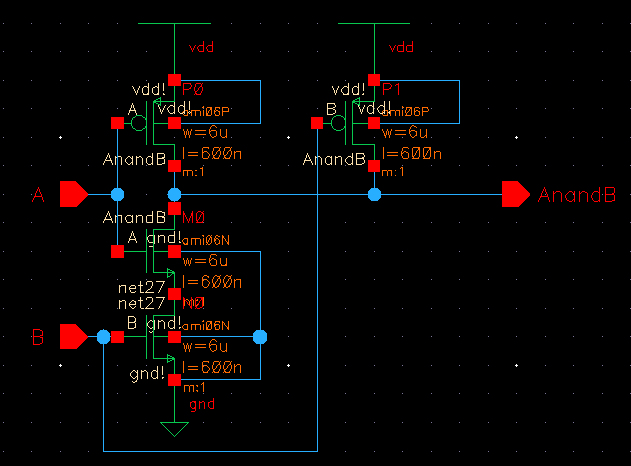
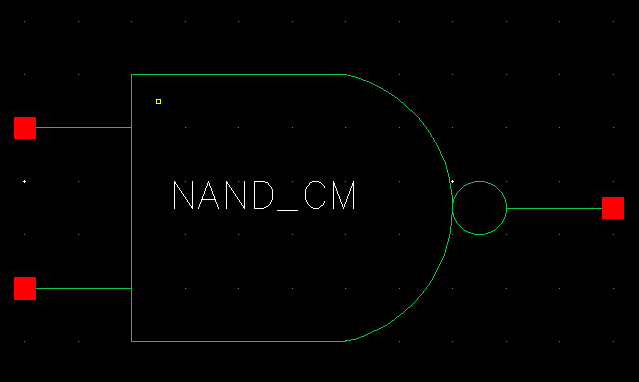
NAND

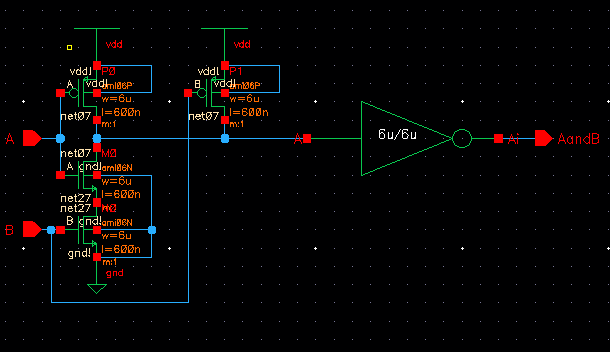
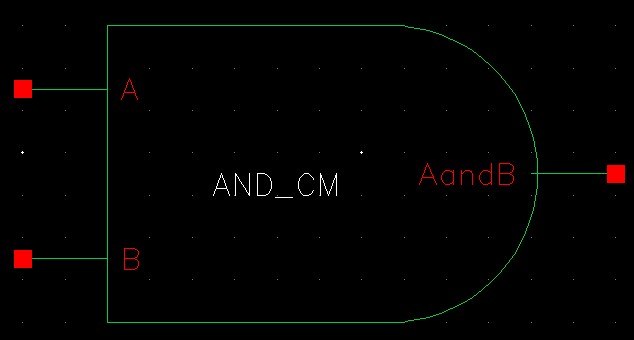
AND
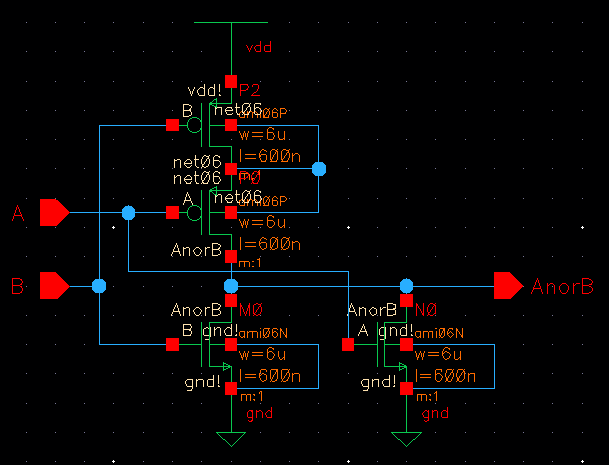
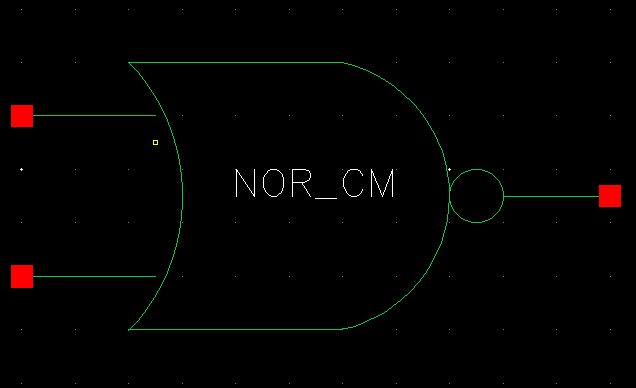
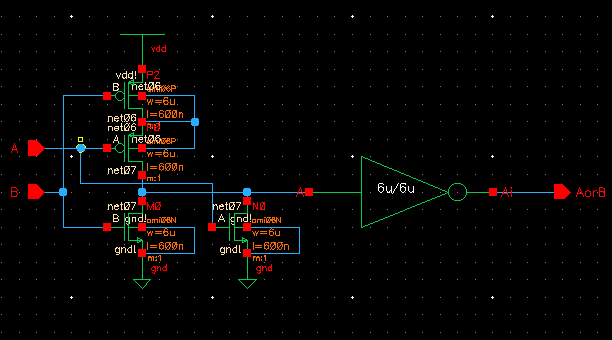
NOR

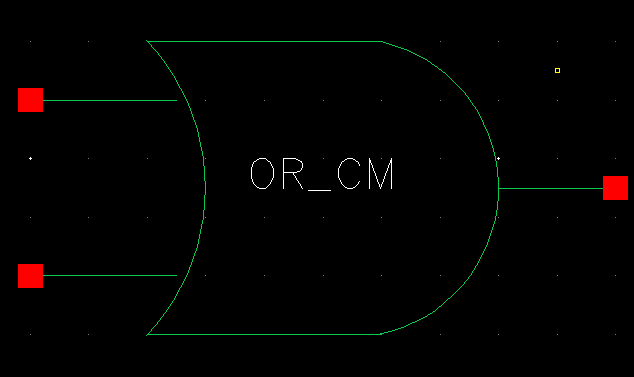
OR



We then took these instances and connected 8bit busses to the inputs and outputs of each termianl as shown below:



NAME
 Schematic
 Symbol
Inverter

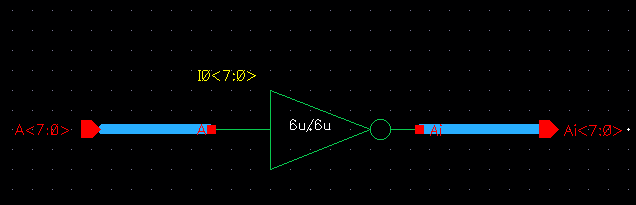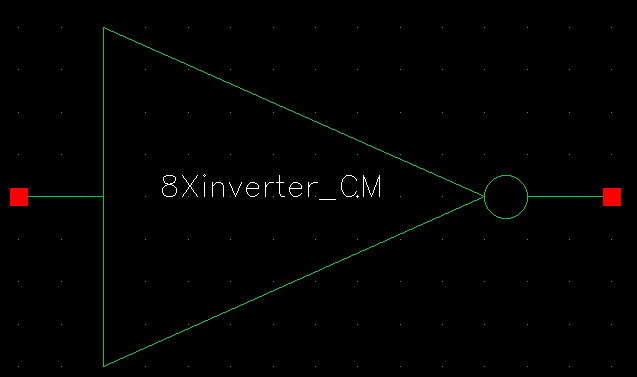NAND

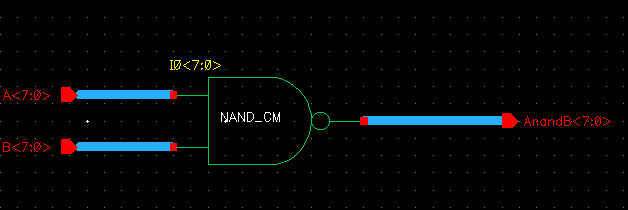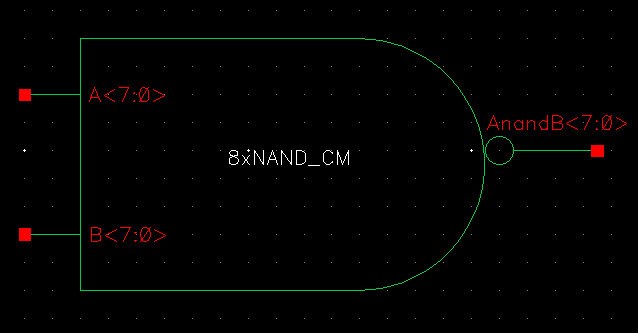AND

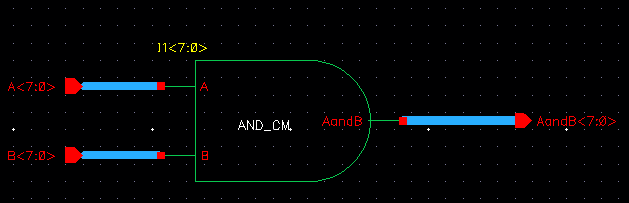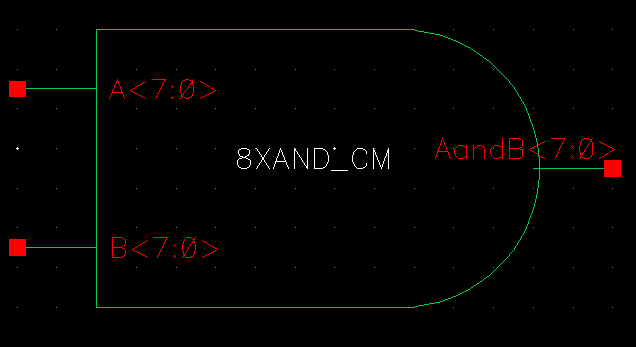NOR

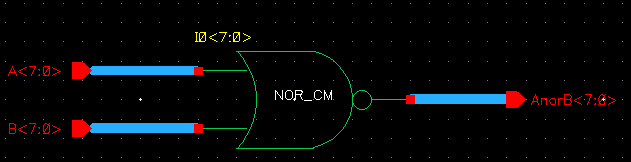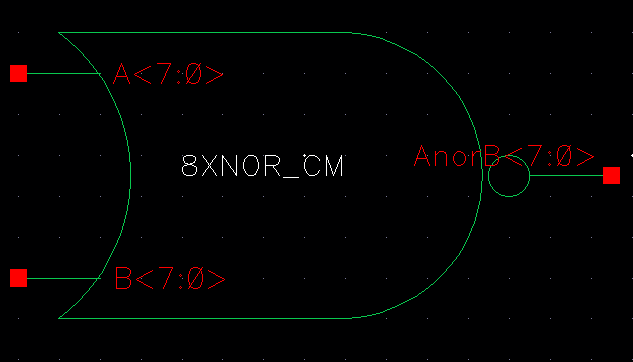OR



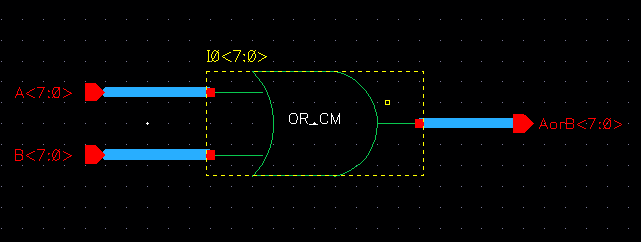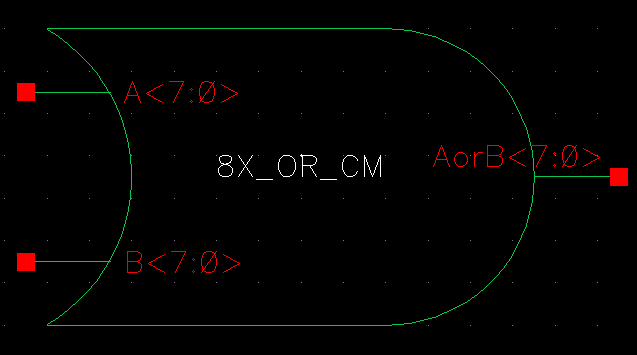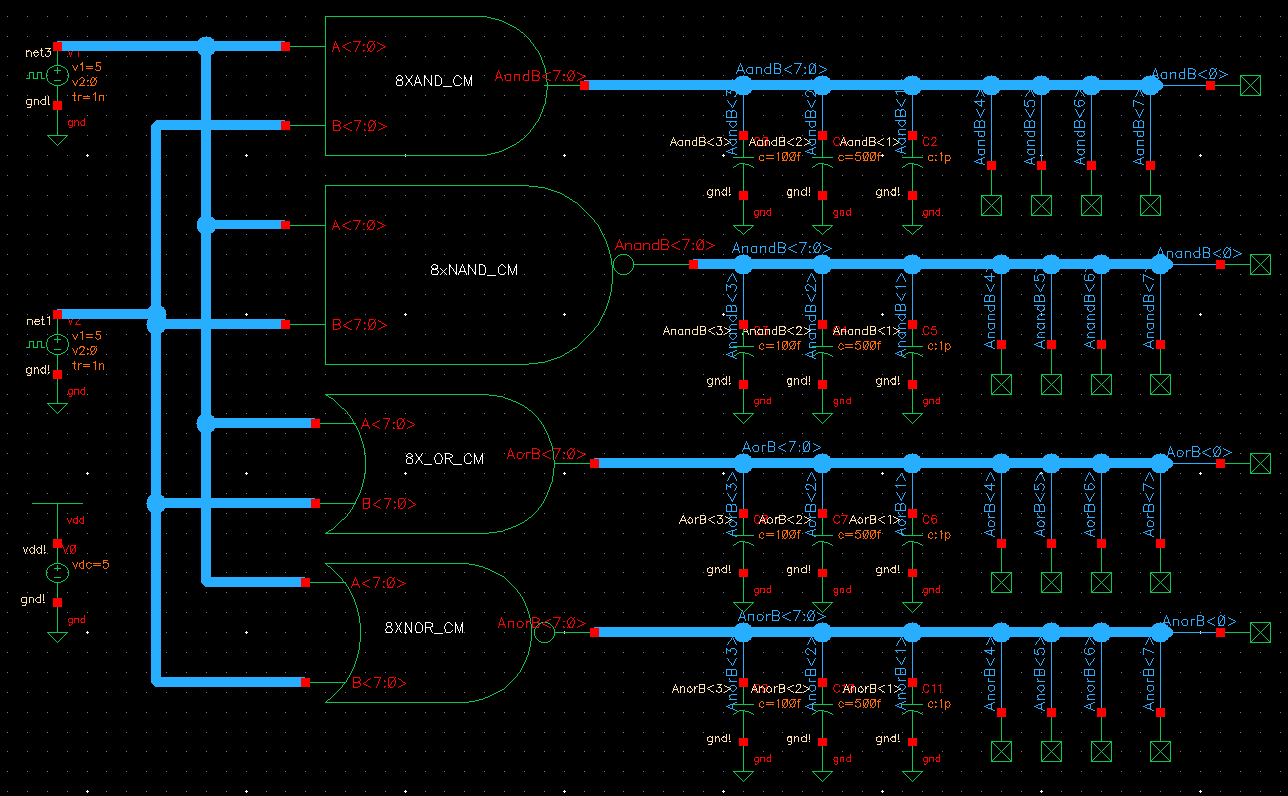
After the above schematics and symbols were created, they where simulated by placing 3 capacitors of different sizes onto seperate branches of the output bus. This is shown below. To perform this be sure to labe the bus as well as each branch created. Even though some of the branches aren't being used they still have to be labeled and connected to no connects for the schematic to pass DRC and sim correctly. The simulation schematics and Sims are shown below:



INVERTER Schematic




AND, NAND, OR, NOR Schematic




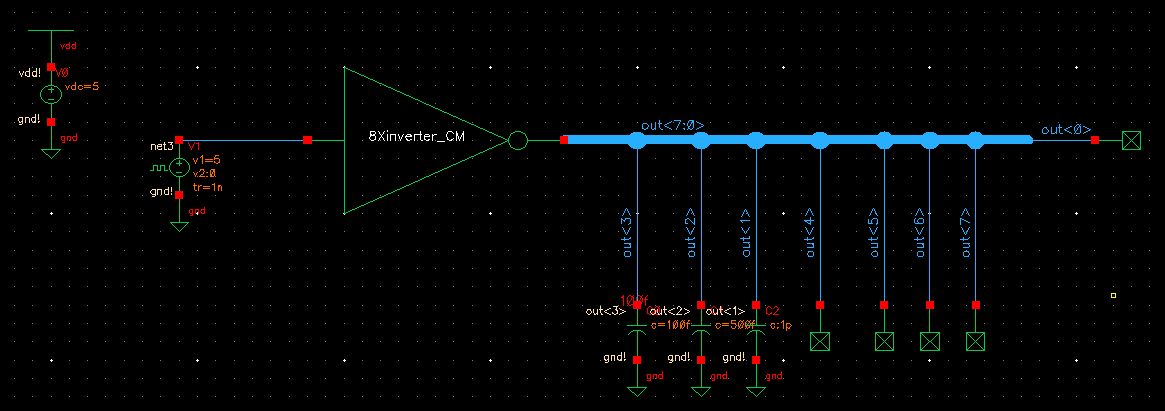
Simulations:

NAME
 Simulation
Inverter
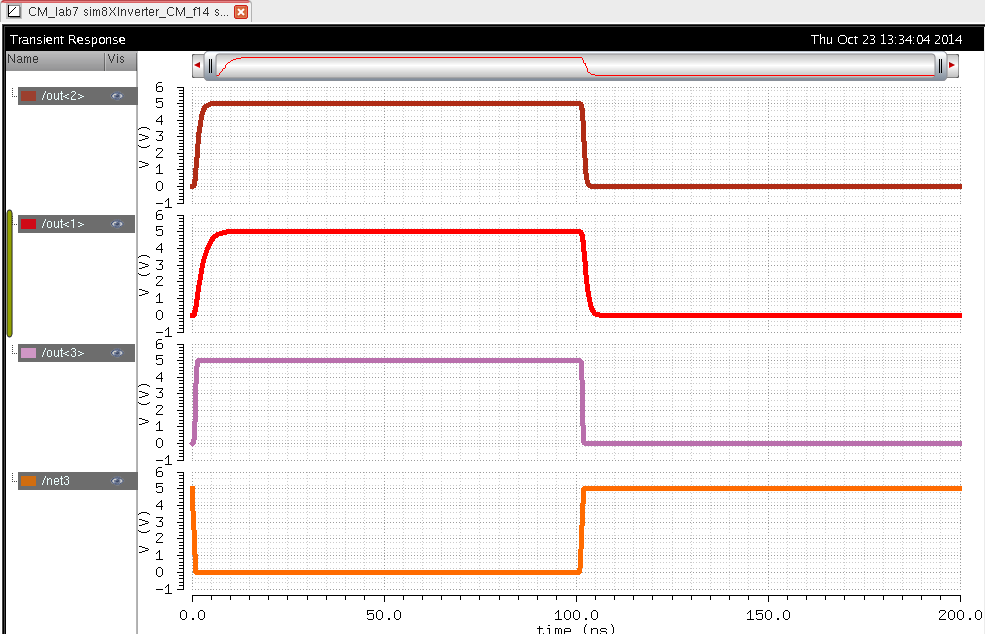AND
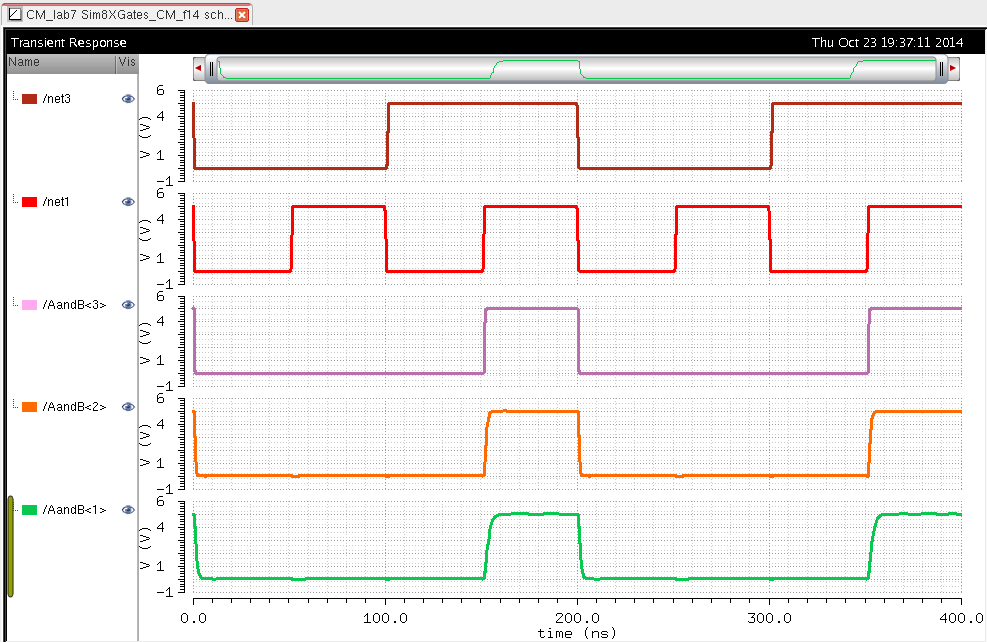NAND
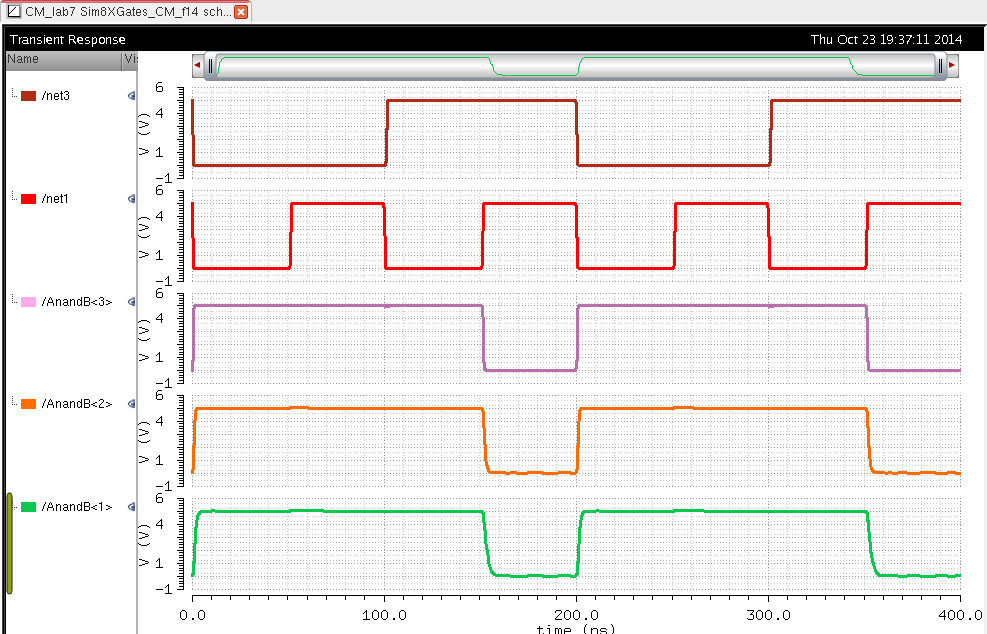OR
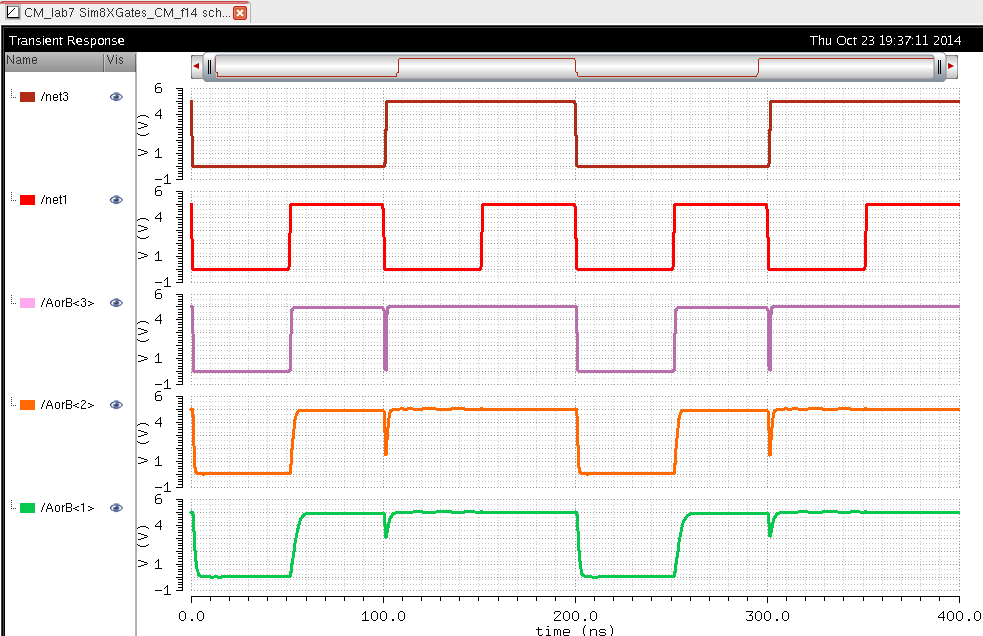NOR


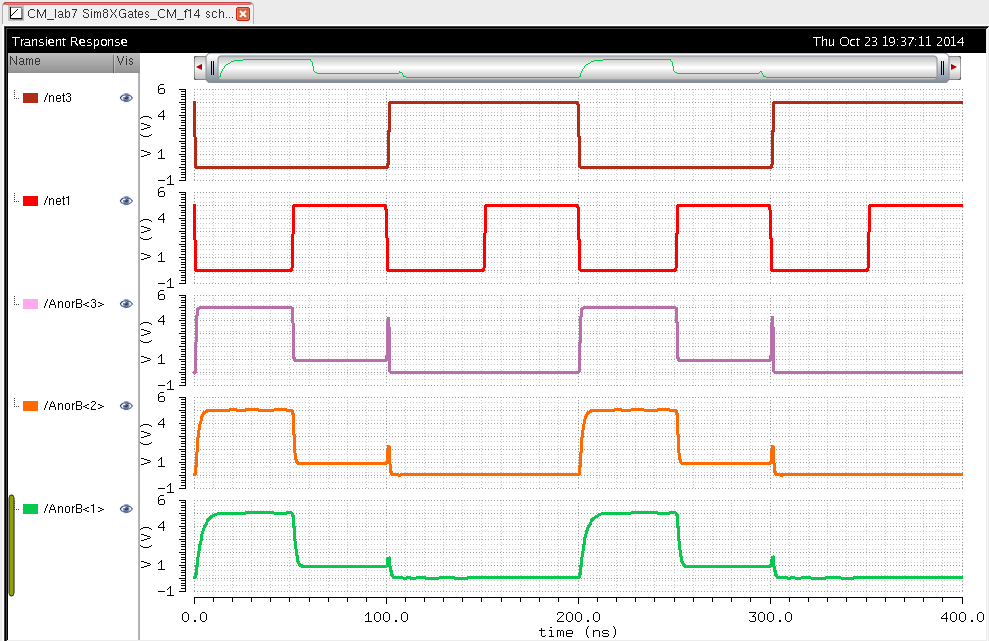The logic for this bit was still correct. As we can see from the simulations when the capacitance is high we get a rounder output with a larger delay. When the capacitance is shorter the shape of the the output is more square like and has a smaller delay. This is very important to know in order to understand how paracitic capacitance can affect the circuit being used.



All the simulations above performed the correct logic for their respective gate. The only wierd effect was the NOR gate which operated correctly but had a voltage of about 1.5 volts when it should have been 0V when A=0 and B=1. 


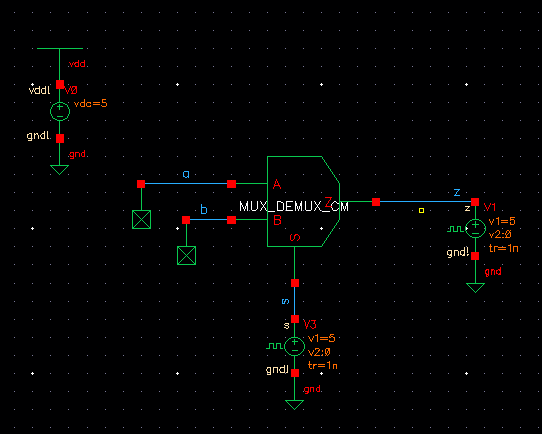
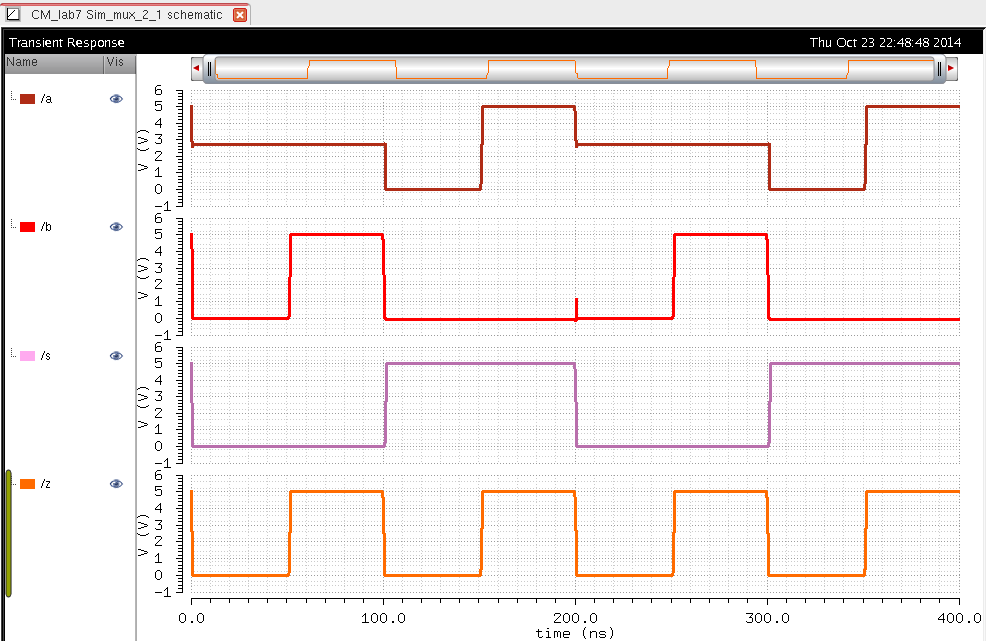
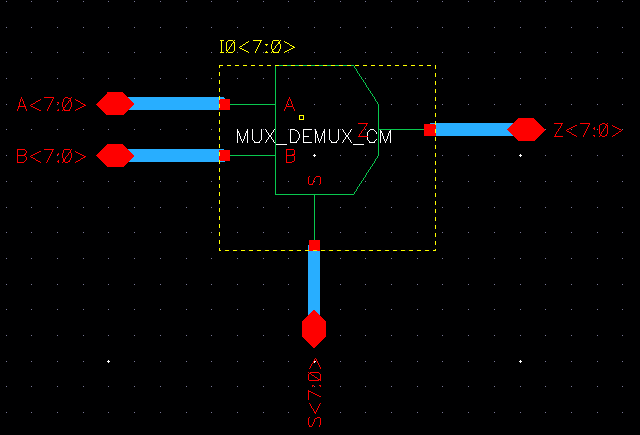
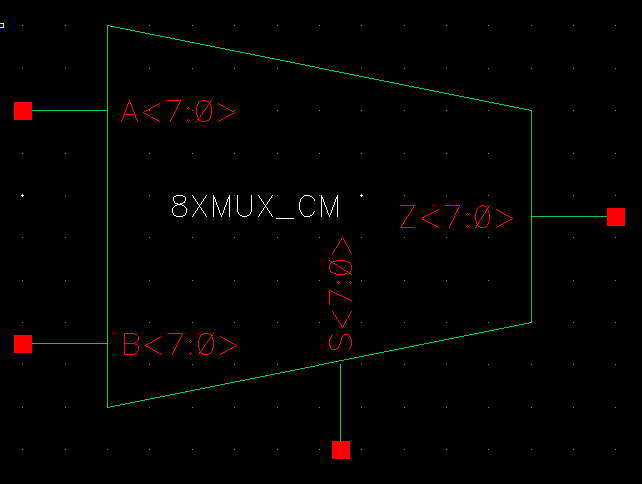
MUX/DEMUX


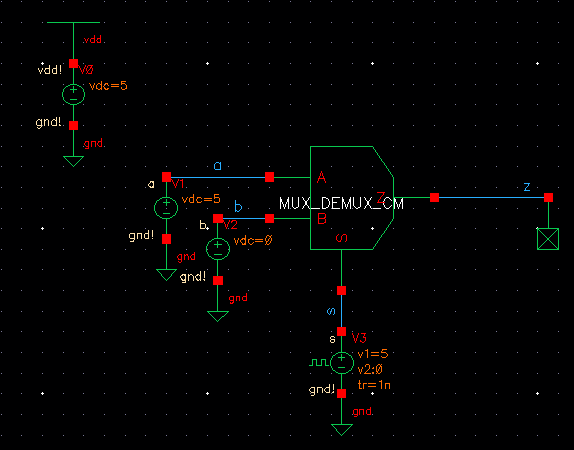
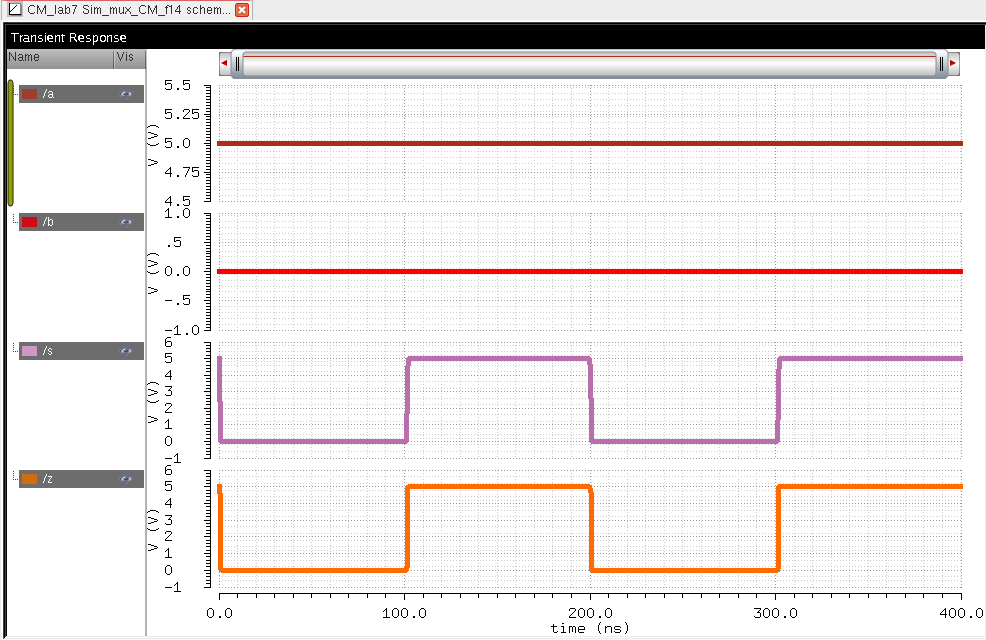
The next part of the lab was to create a MUX gate and a DEMUX using the same schematic. Then to perform the same with an 8 bit MUX/DEMUX. These are shown below:



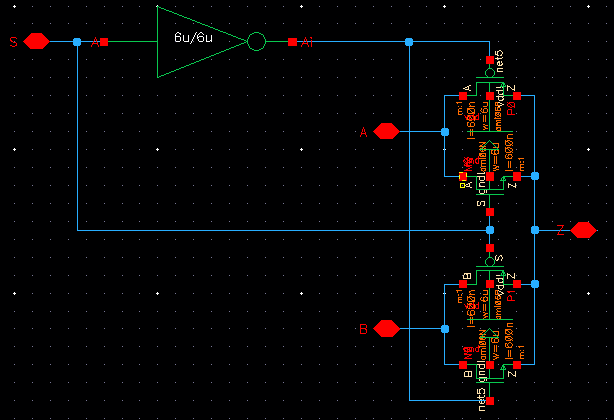
MUX/DEMUX Schematic (Be sure to make all the therminals input/output so that it can be used in reverse)

MUX/DEMUX Symbol

Simulation Schematic
 Simulation
MUX
DEMUX

The way a MUX works is there are two inputs A and B and a selecter bit S. Whenever S is 1 or  0 it allows A or B to be displayed in the output Z. This is shown in the simulation of the MUX.

The DEMUX acts slightly differently. The Z input signal  will be sent to A or B depending on whether the selecter bit is set to 1 or 0. When S=0 the signal goes to B when S=1 the signal will go to B.


8-Bit MUX/DEMUX
Next the 8 bit version of the MUX and DEMUX will be created and simulated as seen below:





Name
 Simulation Schematic
 Simulation
MUX
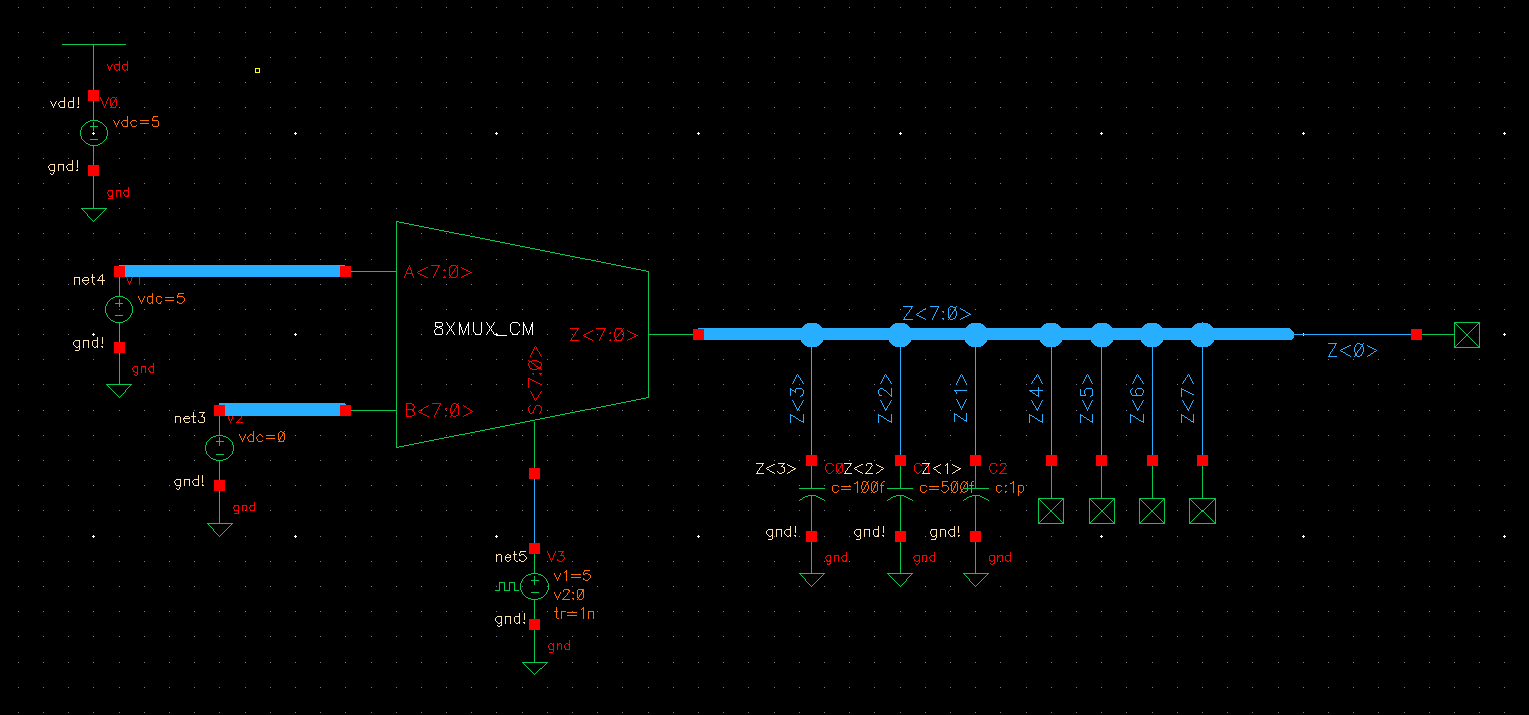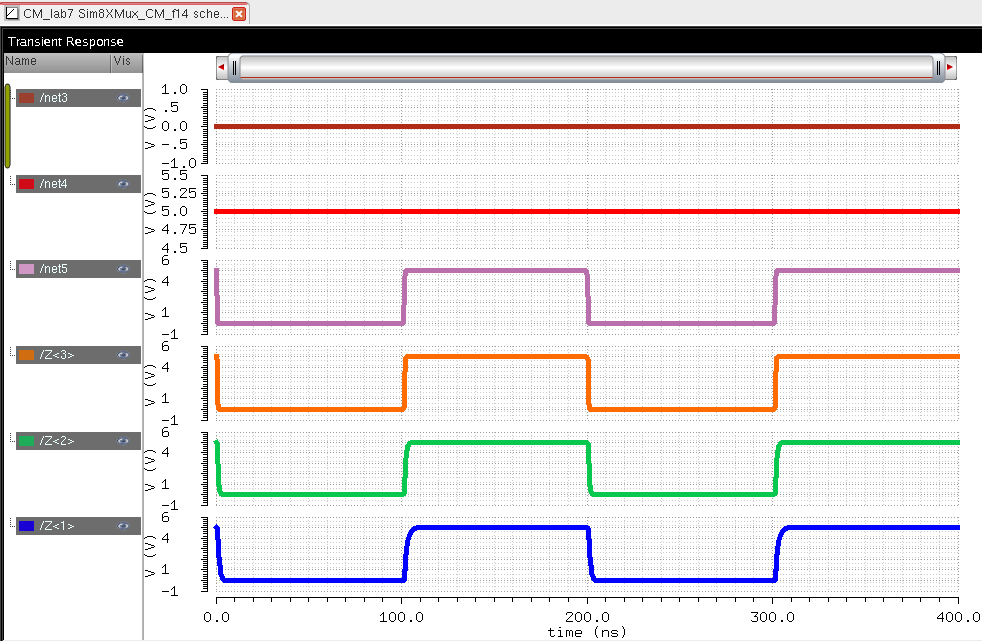DEMUX


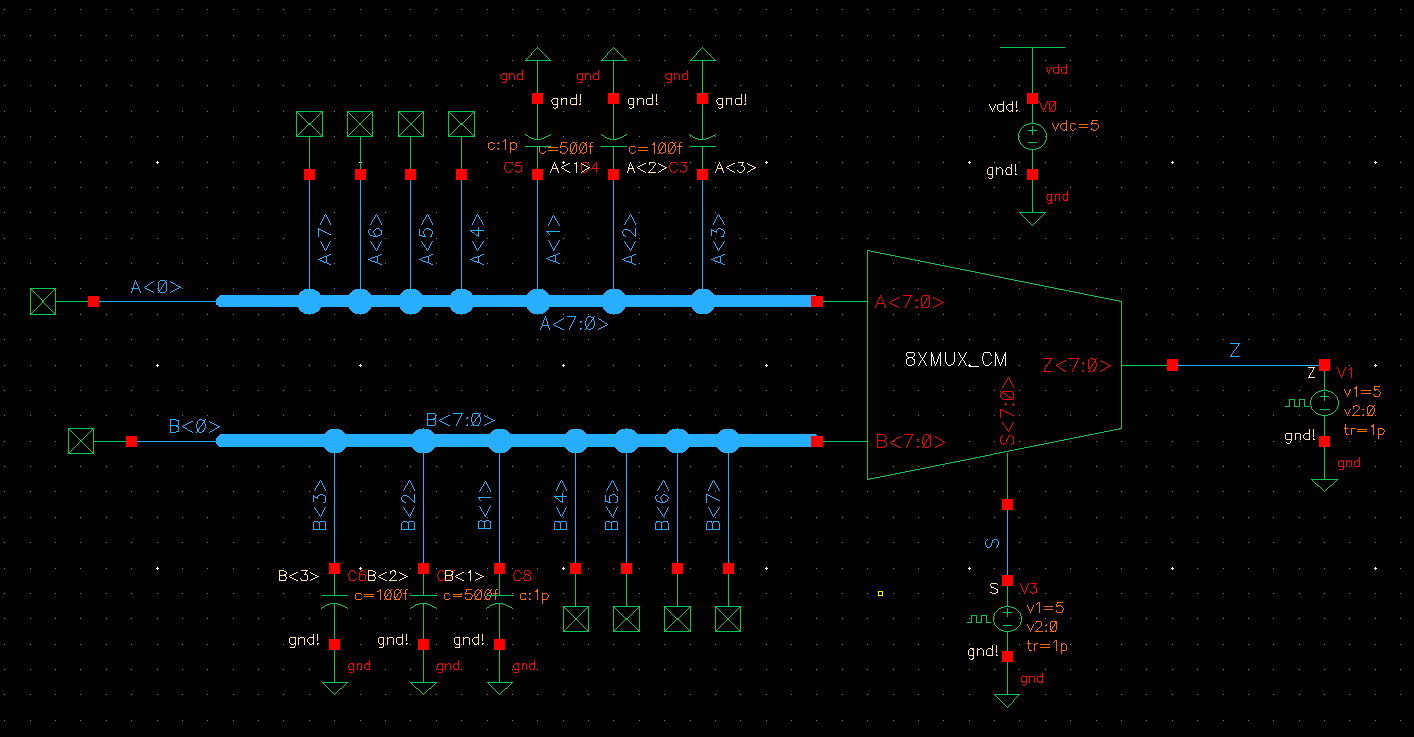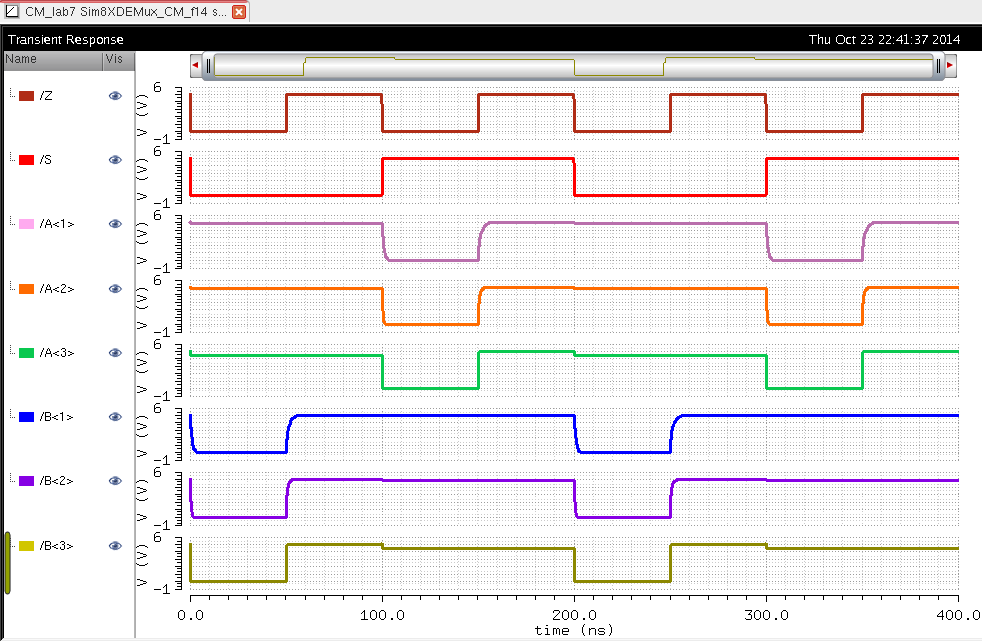As seen above the 8 bit MUX/DEMUX works exactly the same except more inputs and outputs can be connected.




FULLADDER


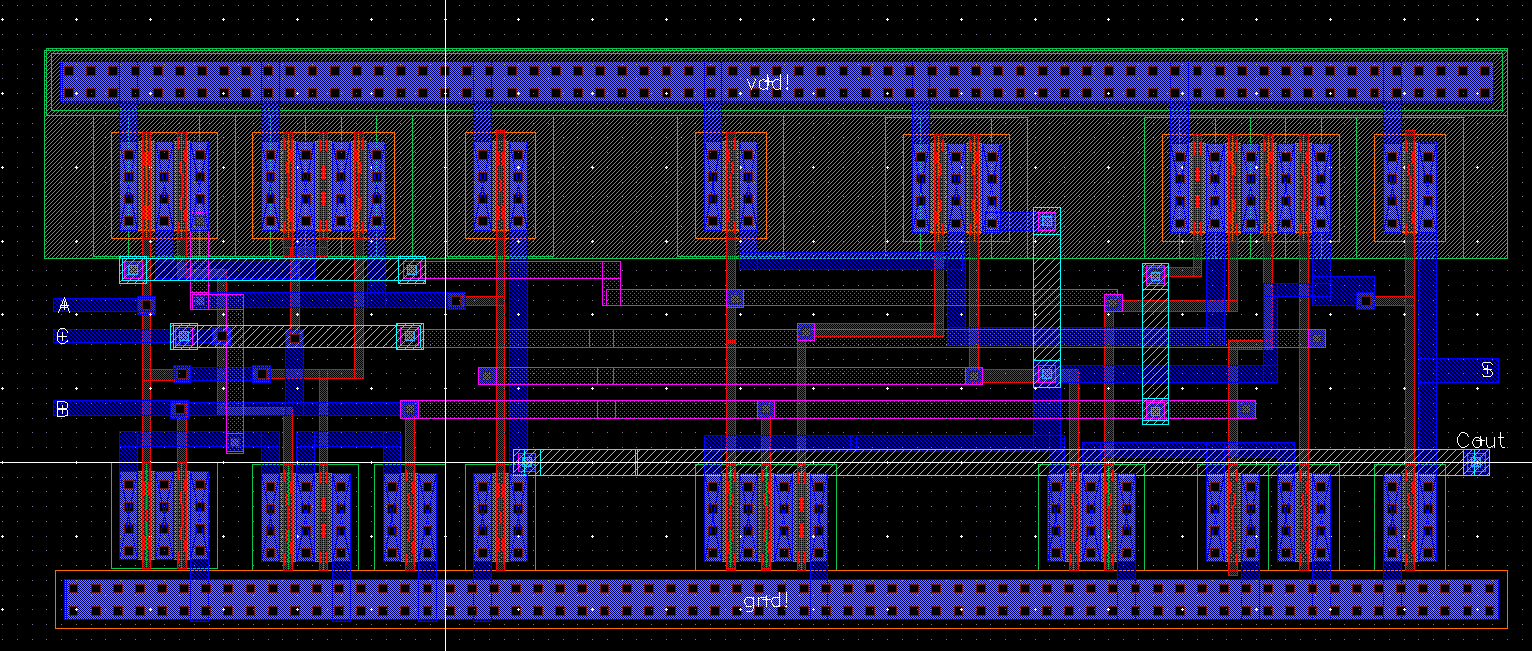
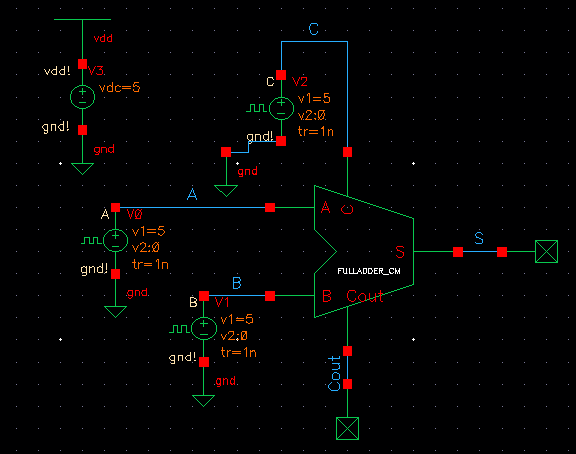
Next we created the schematic and symbol for a full adder as well as the simulation and layout. The operation of a FULLADDER takes an input to A and B terminals as well as a C in bit. These bits are summed together. If the sum has more than one bit than the bit is carried, similar to normal addition. This is shown below:


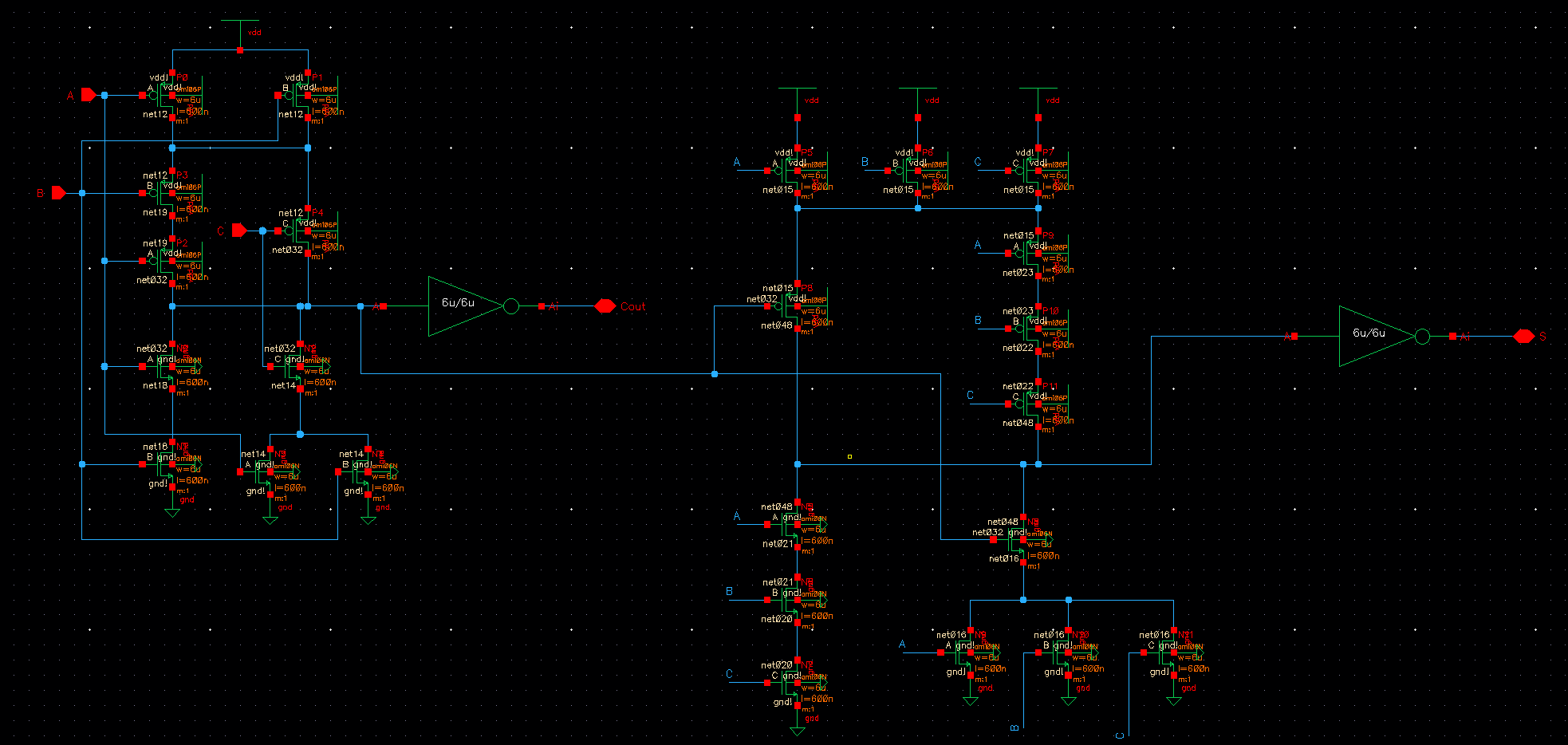
FullADDER Schematic for 1 instance


FULLADDER SYMBOL


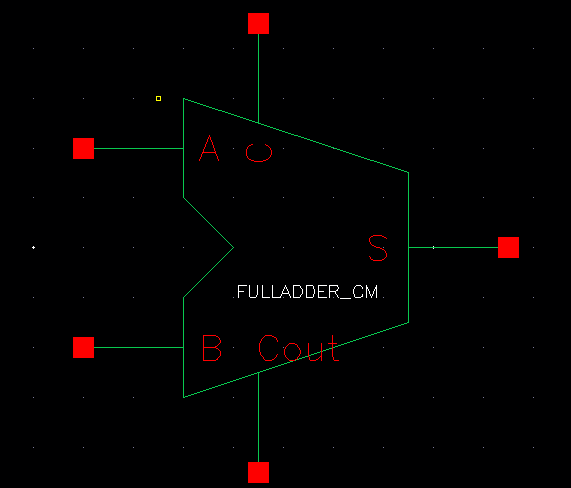
Full Adder Layout



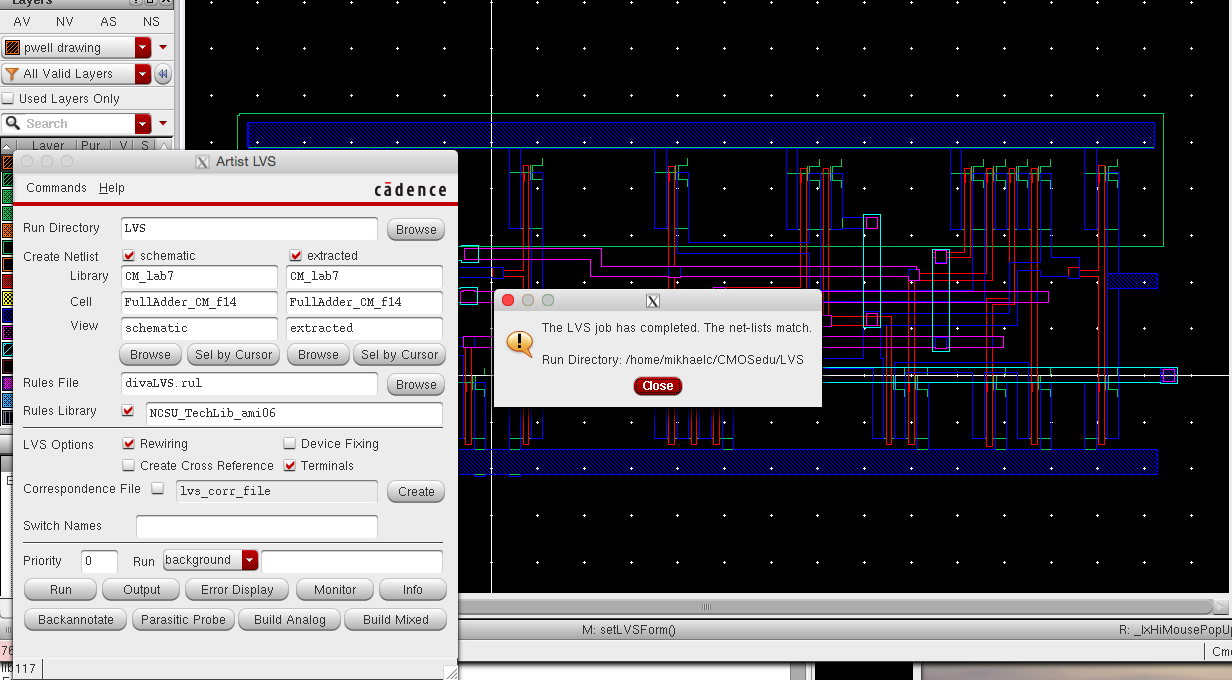
LVS was Sucessfull!!!!!!!!!!!





Simulation Schematic
 Simulation



The adder works as expected example of addition is shown below:

A+B+C:
1+ 0 + 1: Sum=0  Carry=1
1+ 1 + 1: Sum=1  Carry=1
1+ 0 + 0: Sum=1  Carry=0

8Bit FULLADDER

To create the 8 bit adder using the buses we must first understand how an 8 bit adder works. for an 8 bit adder to work correctly the carry of each opperation must be sent to the next adder so it can be summed with the new bits. This is done by connecting Cin with Cout. Since we also want to use buses the connection must be set up logically using the arrays. This is shown below:

Schematic (Notice the notation used at Cin and Cout)

Symbol



8-Bit Full Adder Layout


Front of Layout


End of Layout



LVS


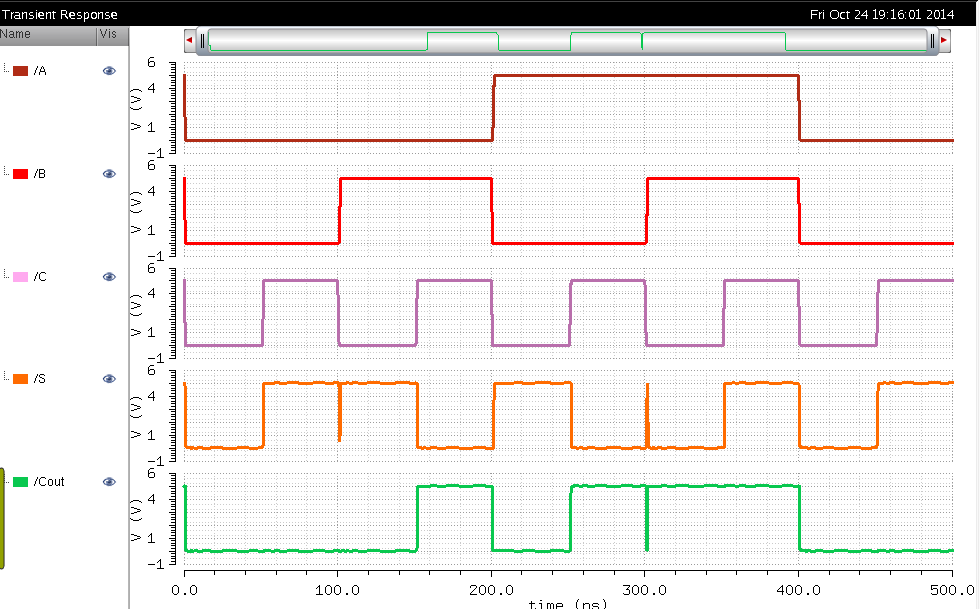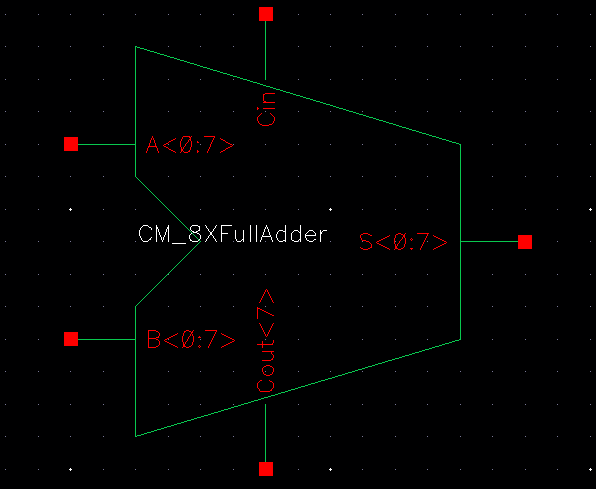
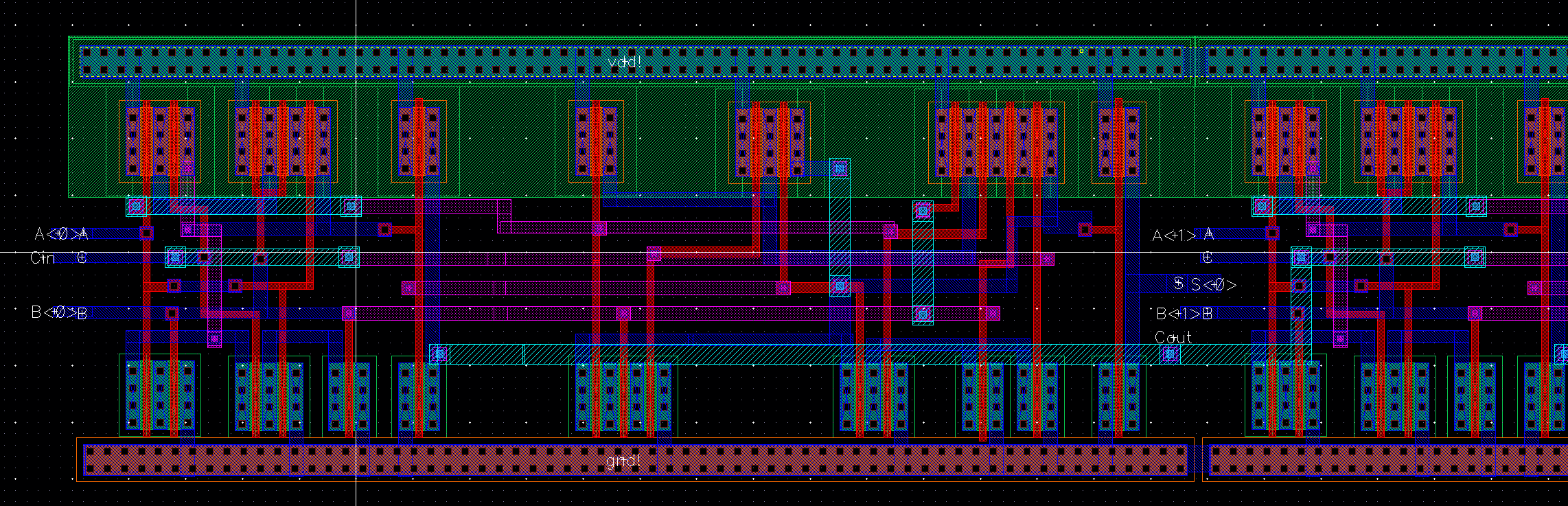
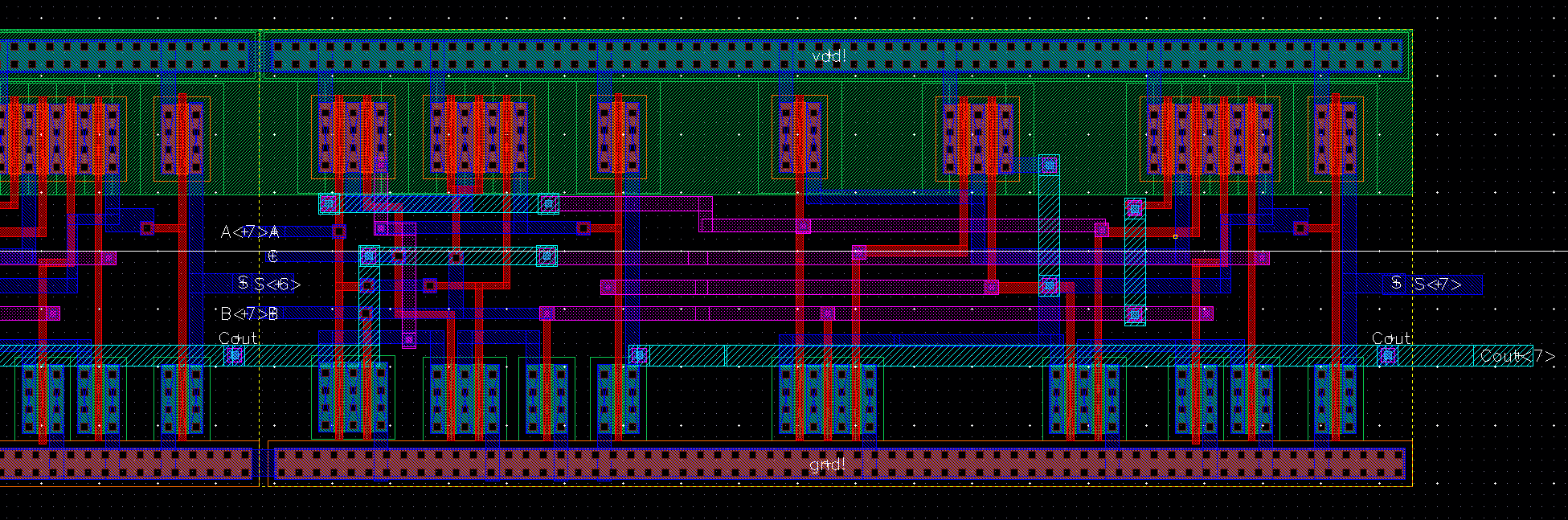
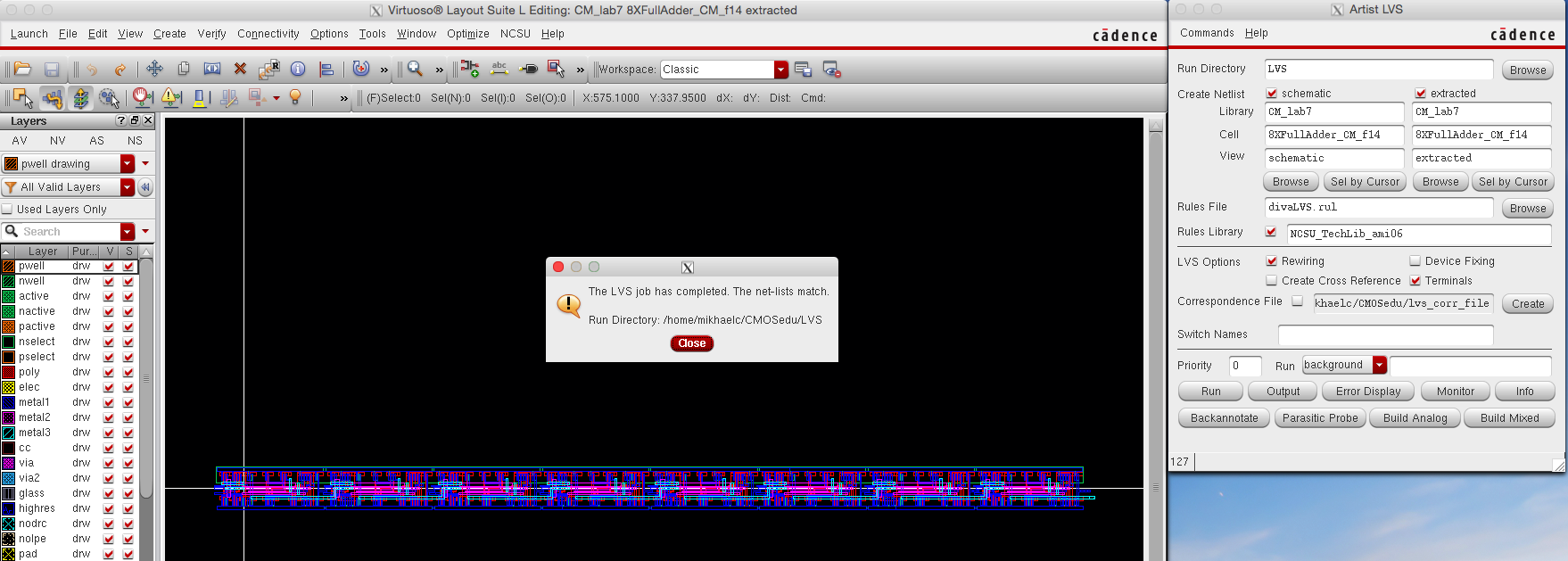
LVS Completed and match !!!!!!!!!!!!!!


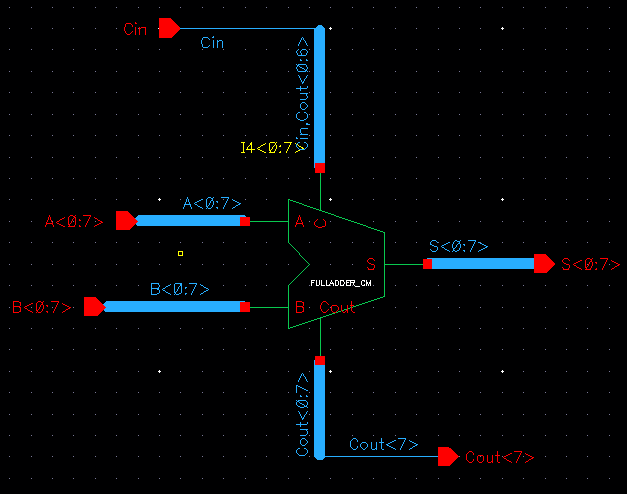
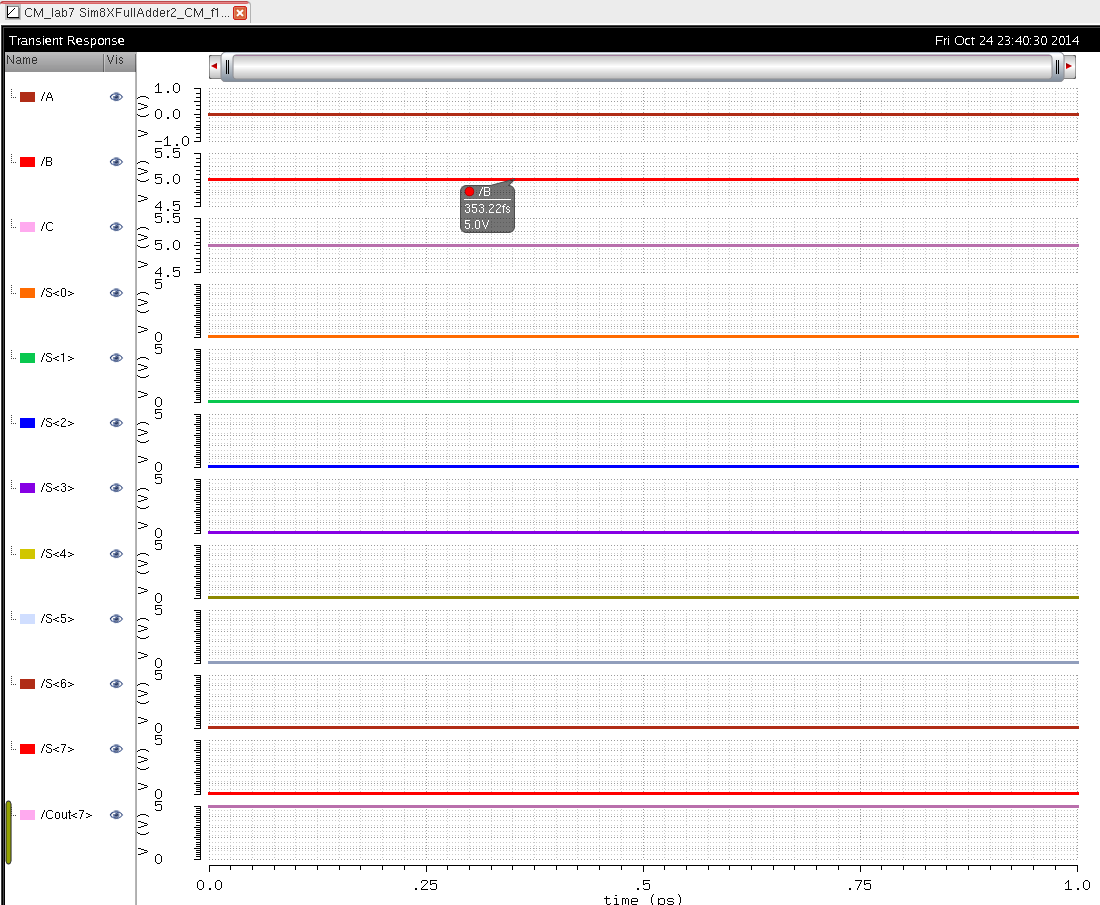
Simulation Schematic of 8 Bit Full Adder(Adding A=00000000 +B=11111111 +C=1)




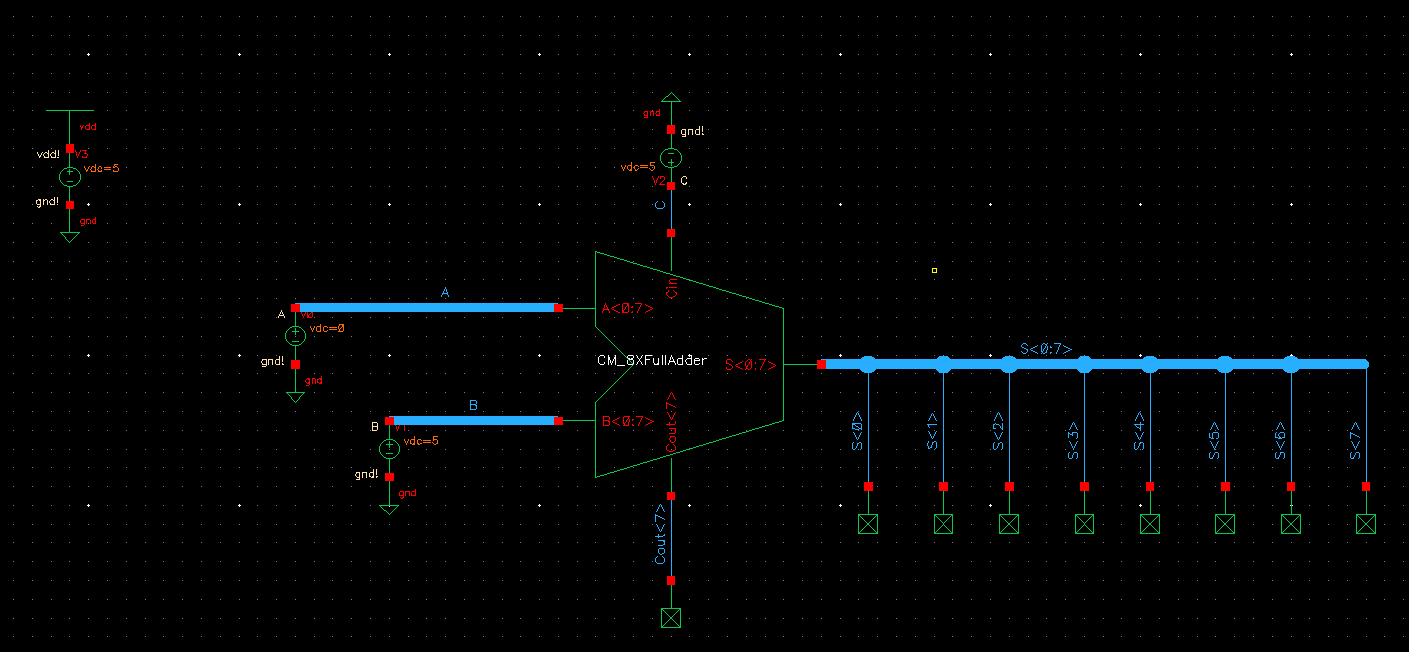
To simulate this we can place any 8 Bit numbeer into A and B but to keep things simple I added A=00000000 +B=11111111 +C=1.

The results should be as follows


     Carry over  1 1 1 1 1 11 11

     Carry Bit                      1

     A                   00000000

   + B                  1 1 1 1 11 11


                       1  00000000


                  Carry    SUM


This is shown below in the Simulation:





Lab 7 directory: CM_Lab7

            

BE SURE TO BACK UP ALL OF YOUR LAB 7 CONTENTS 

(zip and email your work to yourself).