Lab 10 – Final Project

EE 420L Analog IC Design

Lab Date: 4/24/19 Due: 5/08/19 at 5:30pm

By David Santiago – Email: santid4@unlv.nevada.edu

Last Edited on 5/05/19 at 9:22am using Word

Lab description:

After reading, reviewing, and practically building many different types of circuits in the EE420 Analog Integrated Circuit Design Laboratory, we are ready to proceed to do the final project.

In this lab, we will be designing a Voltage Amplifier with at least a gain of 10 using either the ZVN3306A or ZVP3306A MOSFETs, with as many resistors and capacitors that we need. This will be a fast design, and be able to drive a 1kΩ Load and have an Input Resistance greater than 50kΩ and a large output swing as possible. We can also use AC coupling at the input and the output of the amplifier, as long as we can pass 100Hz.

The design constraint is that our amplifier (with no input signal) can draw no more than 1mA from a 9V DC power source.

While building this amplifier, it will be build with the current condition as a high priority.

From studying previous labs and reviewing informational text, the design will be using a Push-Pull Amplifier:

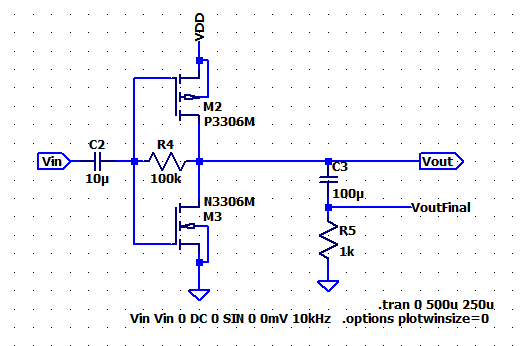
In Lab 6, this type of amplifier can give out one of the highest voltage gains with a very large output swing that goes to about GND and VDD (assuming that the V_DS,SAT and V_SD,SAT are small).

The biggest drawback is that there is no current-limiting resistor in the circuit and we would be relying on the 1/gm resistance of the transistors. Since this amplifier gives out a gain in the 60dB range, the Transconductance will be very large, meaning that 1/gm will be a small resistance (possibly 10Ω), and thus there will be a small resistance connecting from VDD to ground. This means we will have a lot of current flowing through the circuit and we would need to use current-limiting resistors at the top and bottom of the amplifer.

From the above circuit, we get around I_D = 168mA (oops) and a gm = 204mA/V (which means 1/gm = 5Ω!)

Lets add some resistors to our circuit:

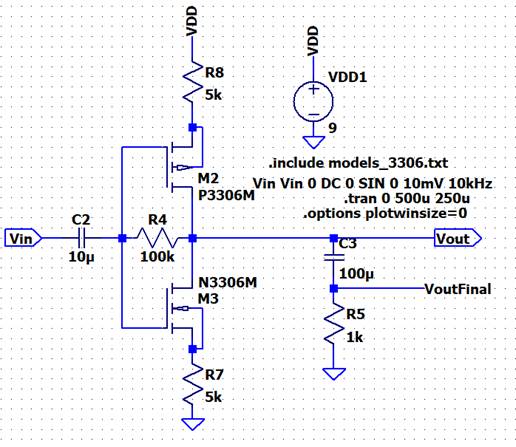
Assuming that we have around 10kΩ series resistance in the branch (plus the higher 1/gm resistance from the MOSFETs) we will get a much lower current of around 9Vx10kΩ = 1mA.

The consequence of having less current through the MOSFETs is that we have a lower gm and gains are decreased, especially when there is a small resistance at the load that will kill the gain.

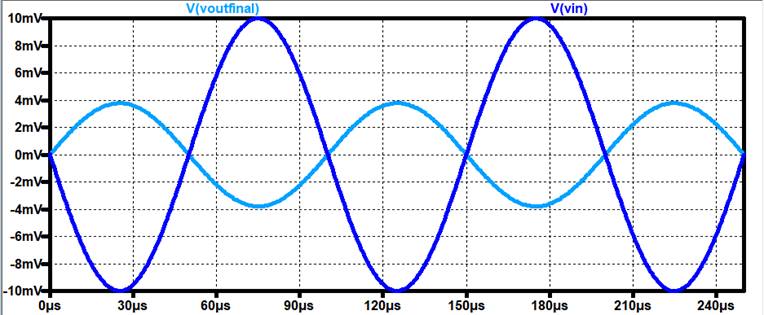
There are a few things we can do to improve this. Suppose we have the Following Common source amplifier:

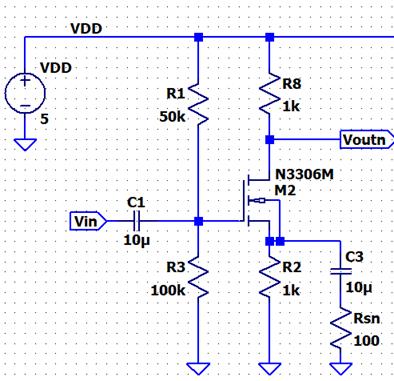
Deriving the gain equation for this topology we get:

V_in = V_gs + i_d(R₂ || R_SN) = i_d * [ (1/gm_N) + 1k||R_SN ]

V_out = 0 – i_d*R_D

V_out/V_in = (-1) [ R_D ] / [ (1/gm_N) + 1k||R_SN ]

= (-1) [ gm x R_D ] / [ 1 + (gm x 1k||R_SN) ]

If we made R_SN = 10Ω, then the parallel resistors at the bottom of the NMOS would practically go to 10Ω (which also means that the node would be near AC Ground) and thus we will have a much higher gain at Vout.

With this in mind, if we add a parallel capacitor at the top and bottom of the amplifier and try to pull the sources of the NMOS and PMOS to AC Ground, we will get a similar outcome.

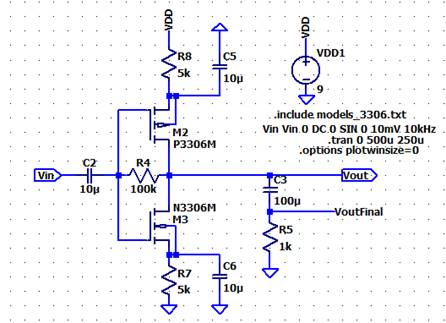
Now we have a much better gain with the 1kΩ Load.

Now the question comes: Why did we get this high increase of gain by pulling the Sources of the MOSFETs to AC Ground?

Lets do some math:

AC Analysis:

Assuming that the current in RBig is 0, Z1 = Rt || (CS1 + RS1), Z1 = Rb || (CS2 + RS2)

I_Out = In + Ip

V_Out = 0 - (I_Out x R_Load)

Equation 1 (Going down and knowing Vgs = id / gmn = in / gmn):

Vin = Vgsn + In x Z2 = (In / gmn) + In x Z2 = In x [ (1/gm) + Z2 ]

In = Vin / [ (1/gm) + Z2 ] = [ gmn x Vin ] / [ 1 + (gmn x Z2) ]

Equation 2 (Going Up and knowing that Vsg = id / gmp = -ip / gmp) Note: id flows down from VDD to GND

Vin = -Vsg + Ip x Z1 = - (-ip /gmp) + Ip x Z1 = Ip x [ (1/gmp) + Z1 ]

Ip = Vin / [ (1/gmp) + Z1 ] = [ gmp x Vin ] / [ 1 + (gmp x Z1) ]

Now With In and Ip,

Iout = In + Ip = {[ gmn x Vin ] / [ 1 + (gmn x Z2) ]} + {[ gmp x Vin ] / [ 1 + (gmp x Z1) ]}

Plugging this into our Vout equation (and making it look nicer):

Vout = - ( {[ gmn x Vin ] / [ 1 + (gmn x Z2) ]} + {[ gmp x Vin ] / [ 1 + (gmp x Z1) ]}) x R_Load

Vout = - Vin x 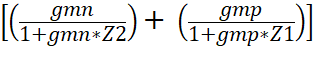x RLoad

And thus, our Voltage Gain for this Push-Pull Amplifier is:

A_V = Vout / Vin = 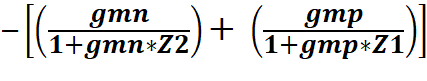x R_Load

What this means is that if we short the top and bottom impedances to AC ground (Assuming that the capacitors are big enough to let AC flow through), then the bottom denominator terms theoretically go to 1 and the gain will be:

Av = x R_Load

This looks very familiar to the Gain equation of the Push-Pull Amplifier from Lab 6, where the gain was determined by the transconductances times Rbig. However, the load resistance will kill the gain to where the big resistance would not make any difference in how much gain we will get. [However if Rbig=0, then it will definitely kill the gain :-( ]

Now with the gain of the push-pull finished, the input resistance will be:

Rin = Vin / Iin

For that, suppose we have this simple circuit model (for viewing purposes):

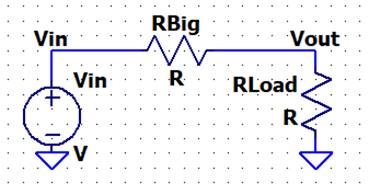
Iin = [ Vin – Vout ] / RBig = [ Vin – A_V x Vin ] / Rbig = Vin x [ 1 – A_V ] / Rbig

Plugging this current into our Rin equation and assuming A_V = 11:

Rin = Rbig / [ 1 – A_V ] = Rbig / [ 1 – 11 ]

= - Rbig/10

Now for the amplifier design, suppose we would like to do a pre-amplifier stage for our Push-Pull Amplifier. A two-stage amplifier is great because the first stage helps to drive the input signal into the second stage so that the Load Resistance does not kill the gain too much and also the gain equation for the amplifier will be:

Av_Total = A1 x A2

For the preamplifier stage, lets use a Common-Source Amplifier:

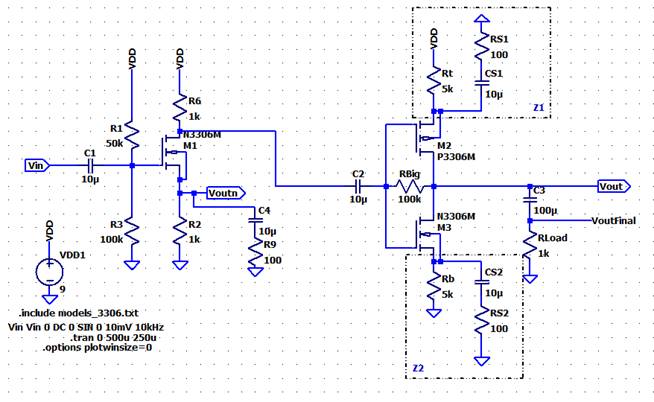
With this stage, we will not only have a higher gain, but the input resistance will not be a function of a gain but rather as a parallel combination of the two resistors at the gate of the first stage amplifier.

The last plus is that we can increase the Resistances of the first amplifier by a ratio and the current can go down but the gain will not since the gain is greatly changed by the small resistor at the capacitor. (And plus the math is a bit nicer at the end)

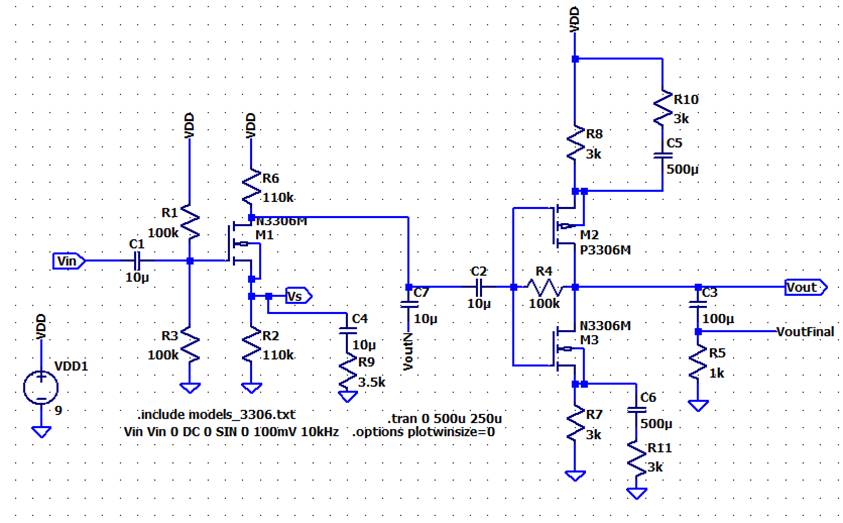
Designing so that there is a gain of 10 V/V and that there is less than 1mA of current:

LTSpice Sim:

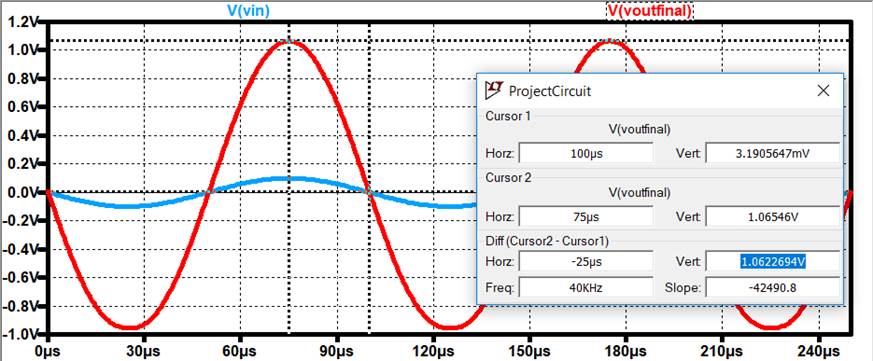
The Gain from LTSpice = 10.6V

AC Frequency Response:

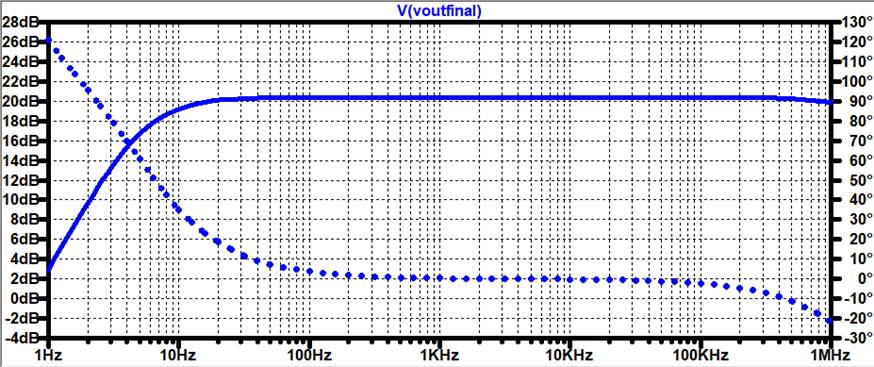
At 10Hz, we start to get 20dB = 10V gain

Hand Calcs :

Characteristics of the Transistor: Kp_N = .1233A/V², W/L Ratio= 1, V_THN = 1.824 V

V_G = 9V (100k) / (100k + 100k) = 4.5V

I_D in the Gate Resistors = (4.5V)/100k = 45μA

I_D = Vs/110k = (1/2) Kp (W/L) (V_GS – V_THN)² = (1/2) (.1233) * (1/1) * (4.5 – VS – 1.824)²

Vs/6.78k = Vs² – 5.352Vs + 7.16

Solving For Vs:

Vs = 2.71V, 2.64V

Solving for the 2 possible V_GS equations (So V_GS >= 1.824V)

V_GS1 = 4.5 - 2.71 = 1.79V, V_GS2 = 4.5 – 2.64 = 1.86V

Finally,

I_D = 2.64V / 110kΩ = 23.4μA

Gm = (Kp) * (W/L) * (V_GS – V_TH) = (.1233) * (1/1) * (1.86 – 1.824)

Gm = 4.5mA/V

Rinput of Amplifier: 100k||100k = 50kΩ

LTSpice:

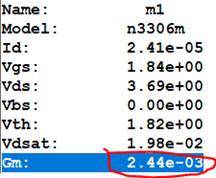
Looking at this, our Hand calcs and Simulations look great!

Now for the Second-Stage Amplifier, the Transconductance parameter is:

Gmp = 13mA/V Gmn = 14.2mA/V, I_D = 683μA

With the Transconductance, we can finally find out the gain of The Push-Pull Amplifier

Input Resistance into Second stage Push-Pull Amplifier :

Rin = Rbig / [ 1 – A_{V2 ]} = 100k / (1 – Av2)

Gain of Av2 (With test voltage Vin of 1V_AC) =

A_V2 = Vout / Vin = 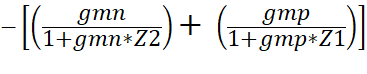x R_Load

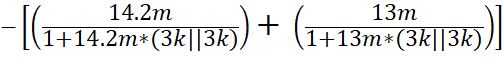= x 1kΩ

= -1.27 V/V Push-Pull Gain

Rinput of Push-Pull = 100k / (1 – (-1.27)) = 44.1kΩ Input Resistance

Gain Equation of First Stage:

V_in = V_gs + i_d(R₂ || R_SN) = i_d * [ (1/gm_N) + R₂||R_SN ]

V_out = 0 – i_d*R_D || Rinput

V_out/V_in = (-1) [ R_D || Rinput] / [ (1/gm_N) + R₂||R_SN ]

= - [ 110k || 44.1k ] / [ (1/4.5m) + 110k||3.5k]

= - 8.7 V/V Common Source Gain

So the overall Hand-Calculated Gain of the Amplifier is:

Av_TOTAL = Av1 x Av2 = (-8.7V) x (-1.27V)

= +11.05 V/V 2-Stage Gain (Non-Inverting)

So comparing this gain to our LTSpice gain again:

We can verify that all theoretical calculations work.

The last condition is to check the DC Current:

Current at the Gate Resistors of Input = 45μA

Current in First MOSFET stage = 23uA

Current in Second MOSFET stage = 683μA

Total Current = 751μA

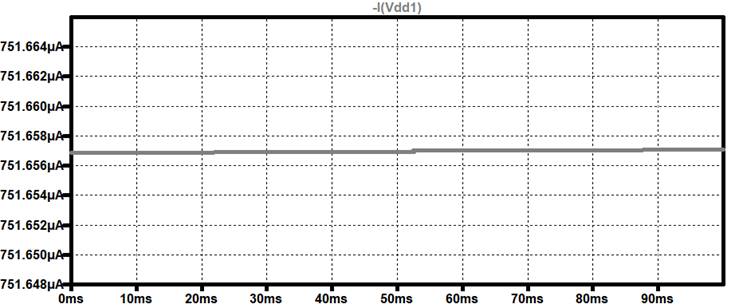
From this, we have met all of the requirements of the Lab Project.

--------------------------------------------------------

Experimental Results:

Note: Some Resistor values were changed so that we can get a gain of 10 V/V

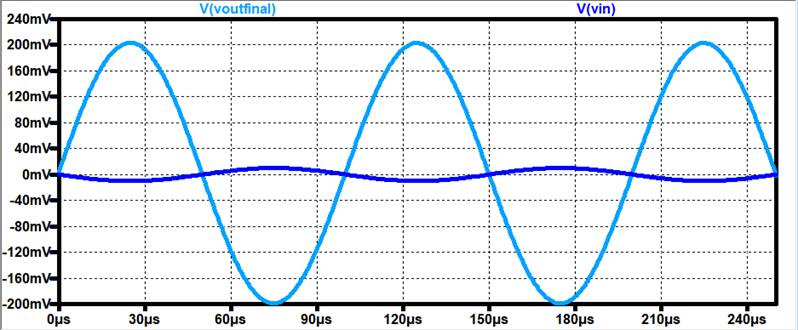
Voltage Gain (At 100Hz):

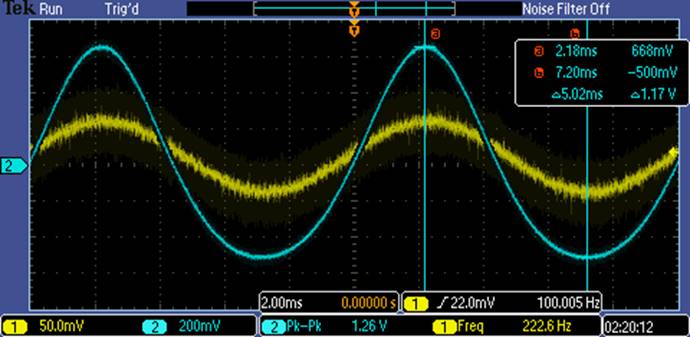
Vout / Vin = 11.7 V/V (Non-Inverting due to a 2-stage amplifier)

From this, we meet the required gain at 100 Hz.

Frequency Response:

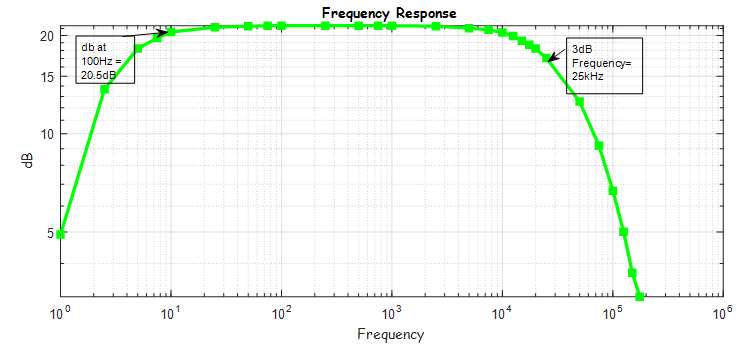
Looking at this plot, the high frequency pole is near 20kHz, which at a practical stance (suppose you were to build a speaker system, and the Human Ear can hear from 20Hz to 20kHz) is a good speaker amplifier.

Maximum Vout Swing:

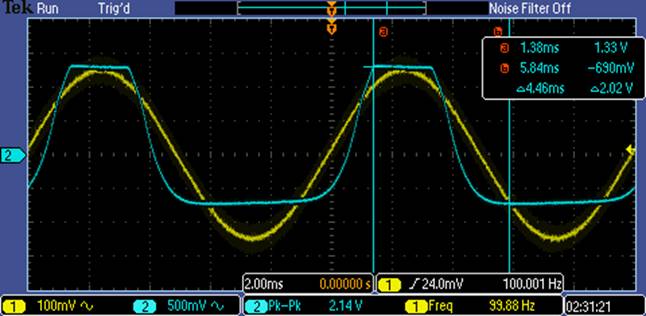
From this, we can see that we have a 2V output swing, and thus we can have a Vin of around 200mV before it starts to clip.

Here is a pic of a 200mV input AC voltage:

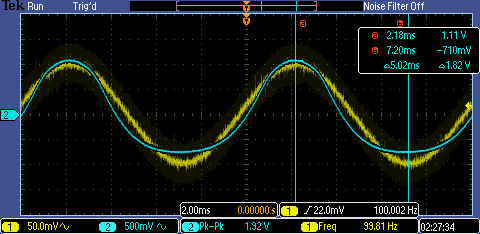
From here, we still have a good gain, but this is the point where Vout will start to clip.

The input Resistance of the Amplifier can be found by placing a resistor at the input and measuring the voltage drop across that resistor.

Inputting a 50kΩ Resistor:

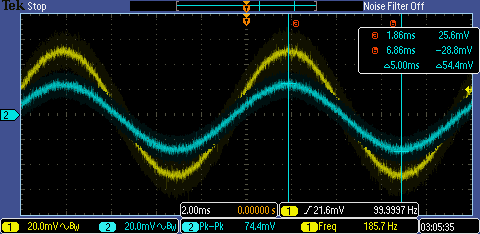
Knowing that:

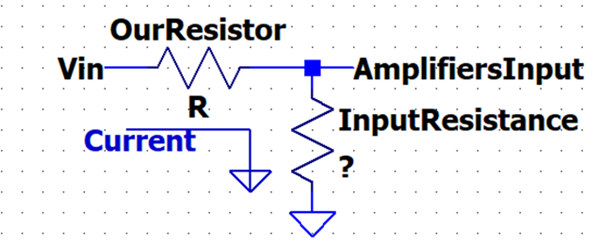
Solving for the total current and doing the Amplifier Input Voltage divided by the Current:

[Vs – Vinput] / 50kΩ = [100mV – 54.4mV] / 50kΩ = 912nA into Amplifier.

Amplifier Input Resistance = 54.4mV / 912nA = 59.6kΩ

This Value is close to our 50kΩ Theoretical Value, but it also passes the required 50kΩ input resistance requirement.

For learning enhancement, here is the slew rate of the Amplifier:

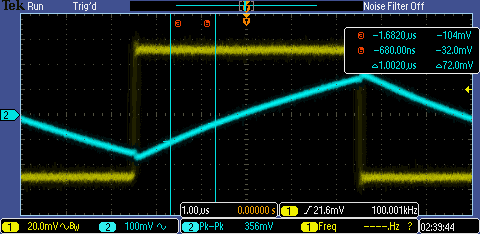
From this we can see that we have a 72mV/μs slew rate.

The final requirement is the Current that the amplifier draws.

From this, we are below the 1mA current and have a current that is around the hand-calculated current.

--------------------------------------------------------------

Conclusion:

The Low-Power Amplifier has shown me that there are many characteristics that must be taken account of such as how the gain equations are strongly dominated by having a heavy (small) resistor at the output. Also, learning to design (and experimentally test) a two-stage amplifier has shown me that there is nothing hidden (no magic), and that hand-calculations can prove to be near what the experimental results look like.

The Analog IC design Laboratory has taught me skills that will help with future research or in the Industry. From characterizing CMOS Transistor Trays to compensating a scope probe, this lab class has shown me that there is much more to learn and many things that can enhance (and worsen) designs in microelectronic circuits.

- Sources:

CMOSedu.com accompanied with: CMOS – Circuit Design, Layout, and Simulation

Return to EE 420L Labs...