Lab 2 – Operation of a Compensated Scope Probe

EE 420L Analog IC Design

Lab Date: 1/30/19 Due: 2/06/19

By David Santiago – Email: santid4@unlv.nevada.edu

Last Edited on 2/06/19 at 1:11am using Word

Lab description: In this lab, we will be learning about how to properly compensate a scope probe, and also compare different types of compensated cables using simple circuits.

When we are testing our nice circuits for voltage outputs, we want to know what is truly being outputted from a circuit. In the DC world, our oscilloscope will show us what is happening on the board, however, when testing for AC, there may be some slight variations for when we go to higher frequencies. Our probes are not perfect and contain a Parasitic Capacitance and we need to try to work around this nasty little obstacle. A Compensated scope probe will help us try to eliminate that parasitic capacitance so that we can accurately get what we see from an AC circuit, but the takeaway is that we will get maybe a 10^th of the output into our Oscilloscope. To fix that error, we change the Oscilloscope’s attenuation to do some “math” and give us our desired output.

--------------------------------------------------------

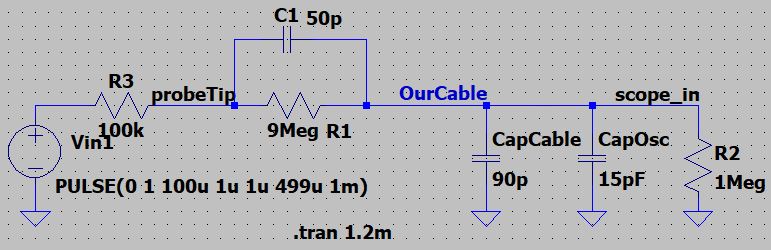
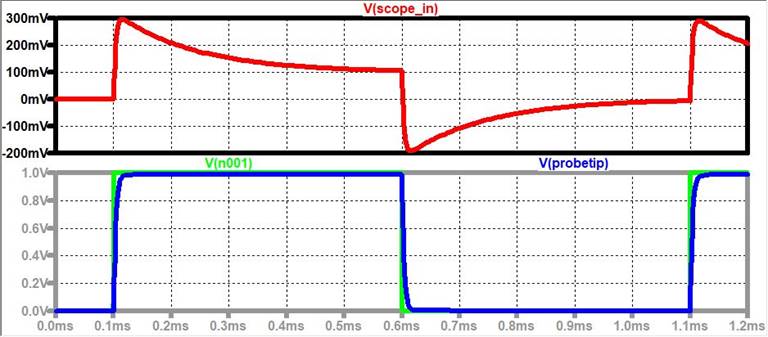
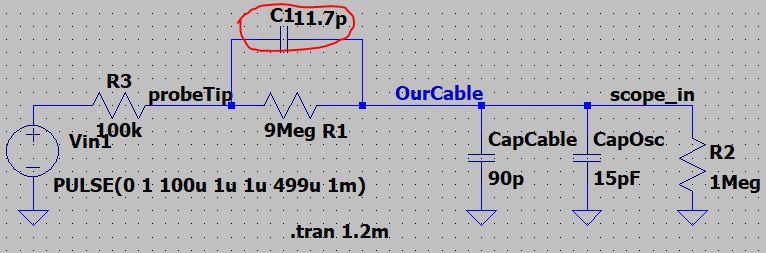
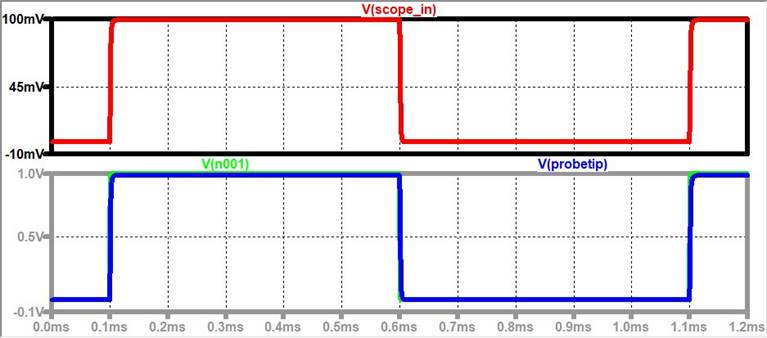
Experiment 1: 10:1 Probe Pic

Here we will be showing what types of compensating probes we can get.

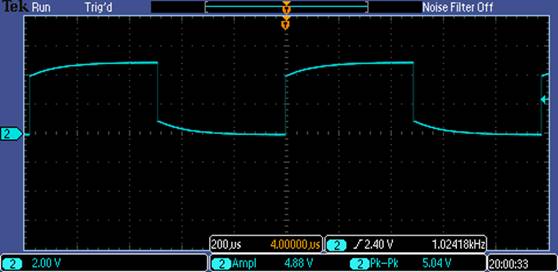
Undercompensated Probe:

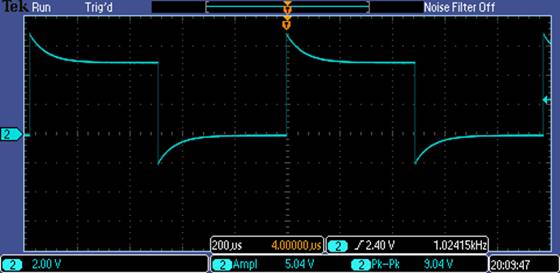
Overcompensated Probe:

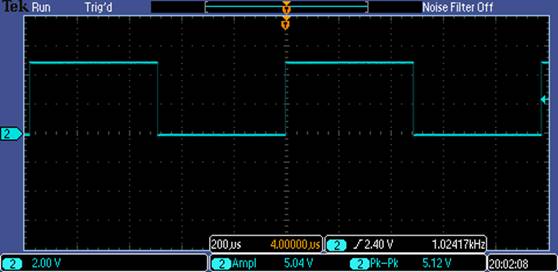
A Nice Compensated Probe:

Comment on the Probe:

The reason for the undercompensated probe is for the capacitor being too small at the probe tip.

LTSpice: C1 =1pF

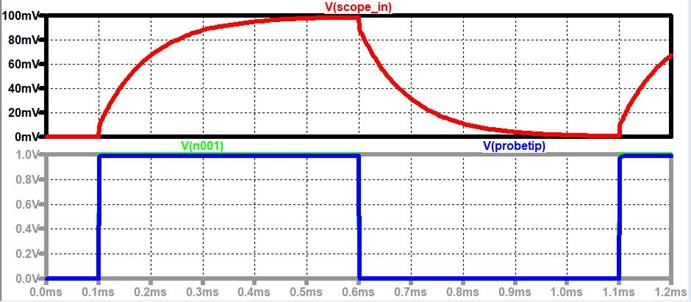
For the Overcompensated probe, the capacitor is too big at the probe tip.

LTSpice: C1 = 50pF

It makes sense looking at the Overcompensated Probe that the Output spikes up because if we assumed that C1 is super BIG, the current will fully pass through the capacitor and the scope_in voltage will equal the probe tip voltage.

Going back to the Undercompensated Probe, the opposite will occur and we will have it to where the voltage will slowly climb up.

For the Nice compensated probe, we will have a clean signal at the scope_in that will look like what is being seen at the probe tip.

Comment on the type of Scope probe:

On the Scope, we have the attenuation set to x10. The probe is a 10:1 probe, which means that the voltage that travels through the cable is a 10^th of the voltage that is on the Probe Tip. Once the 10^th of a volt gets to the input of the oscilloscope, the oscilloscope does a simple math multiplier of 10 so that the voltage that on the probe wire mimics the voltage that is at the Probe tip.

Probe Tip Attenuation:

Here, this special probe can either be set to x1 or x10 attenuation. If set to x1, the voltage that is on the Probe tip will be the same on the probe wire cable. If set to x10, then the impedance at the tip will drop the voltage to a 10^th of the voltage at the probe tip.

Oscilloscope Menu:

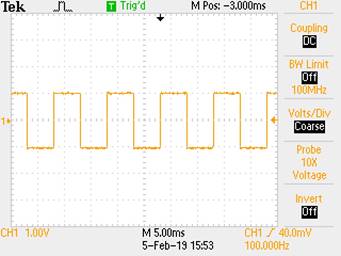
Here we can see that our Probe attenuation is set to x10, and we are getting a 1V amplitude read on the screen. This also means that the voltage that is actually received by the oscilloscope is really a 10^th of a voltage from the Probe tip.

--------------------------------------------------------------------------------------------------

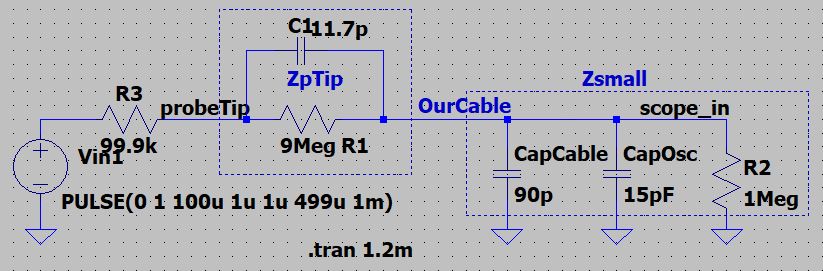
Maths and all That (Our Draft of The Circuit):

So are we really telling the truth that there is at least 0.1 Volt seen at the scope input?

Lets do some very simple math…

BEFORE THAT:

First we need some simple theory. We will be creating a voltage divider, to where we want a 10^th of a volt at the Output. So, we start off with:

Z_ProbeTip = 9 * Z_Small

Assuming that the Source Voltage and Probe tip are at the same Voltage potential (So very low Current):

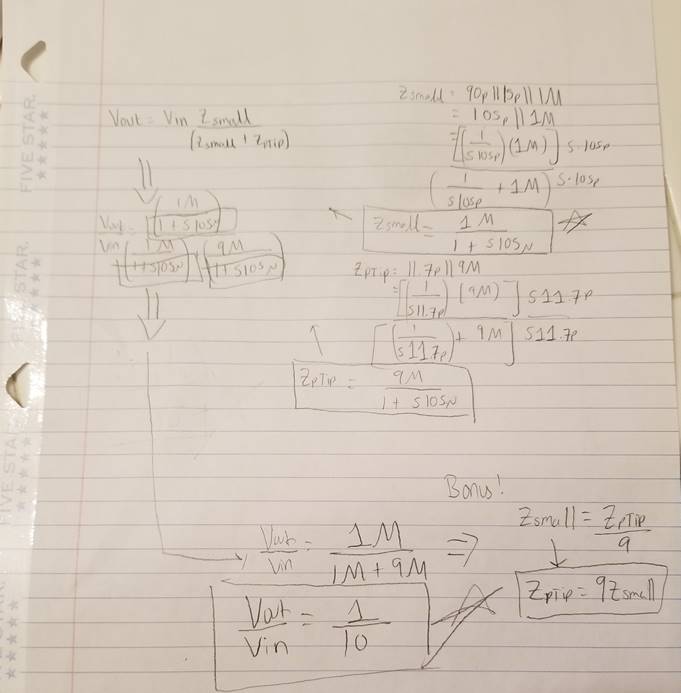
The whole point of the hand calcs was to prove that if Ztip = 9 * Zsmall, that the voltage at the input of the scope will always be 0.1*Vin.

IN OTHER WORDS:

R_Probe = 9*R_Scope , ZC_Probe = 9 * ZCsmall --> C_Small / 9

---------------------------------------------------------------------------------------------------

Experiment 2: Solving for the Parasitic Capacitance of the Cable & Probe

For this Part of the experiment, we will be doing a super simple circuit, and that is the RC time constant circuit.

By remembering that one Time Constant is equal to about 63% of a voltage input, we can measure the time constant on the Oscilloscope, and knowing the Resistance, we can experimentally solve for the Capacitance of the cables.

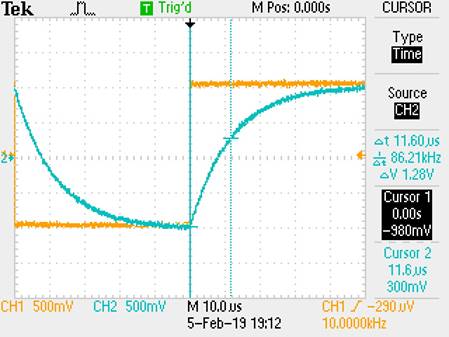
Oscilloscope Probe Capacitance:

R = 99.9k, Vin = 1V, freq = 10kHz

One time Constant = 1.6us

T = RC

C= T / R = 8.4u / 99.9k = 84.1pF Oscilloscope Probe Cable

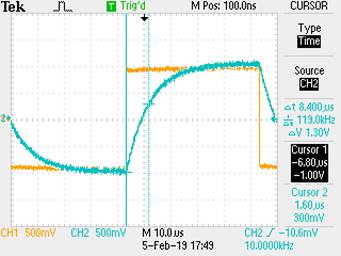
Measured Capacitance of Probe from LCR: 85.5uF

Power Cable Capacitance:

One Time constant = 11.6us

T = RC,

C = T/R = 11.6u / 99.9k = 116pF Power Cable

----------------------------------------------------------------------------------------------------

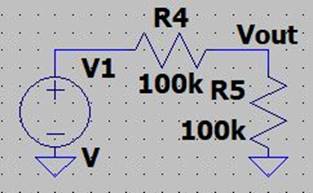
Experiment 3: Voltage Dividers!

For this Experiment, we will be going high speed and testing out 2 different cables:

-An uncompensated Power Cable,

-A nice compensated Oscilloscope probe cable.

Here is our Very simple circuit:

We will be doing this at freq = 1MHz, so that we will be able to see the effects of the cables’ capacitances.

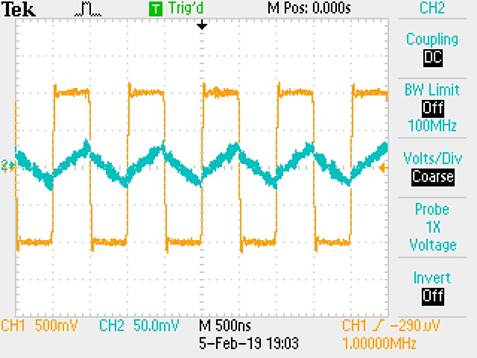
Uncompensated Power Cable:

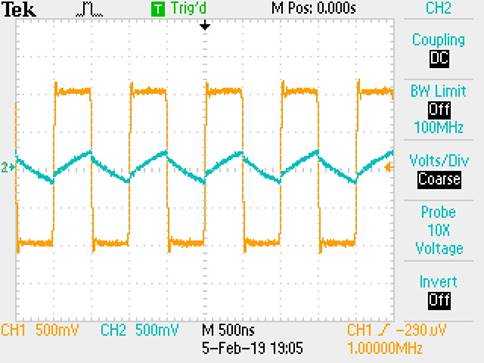
Compensated Oscilloscope Probe Cable:

Observations:

For the Uncompensated cable, we can see that there is some nasty noise that we do not like in our cable, and that it is fairly accurate, however, we used about a 1-meter wire, which can correlate to ~100pF/meter. This means, it will somewhat look like our compensated probe, however, with some noise and maybe not as high of an amplitude since it will need more time to charge up with the RC time constant. Also, the Attenuation is set to x1.

For the Compensated Probe cable, there is a cleaner signal and that it is a bit higher than our uncompensated cable. The Impedance from the probe tip helped clean up the signal so that we can be more accurate at the scope input. Even at a 10^th of a volt, this is very accurate and even though there can be some more fine tuning at the probe, our result is acceptable since at a smaller capacitance, we will get some zero points at the Megahertz range.

------------------------------------------------------------

How to implement a test point on a PCB given the length of a cable:

For this, if given we do not have a probe tip at the end of our cable, we can build our own probe tip on the PCB! For that, we will set it up to where we have calculated the capacitance of the cable and the scope input, and to make Z_PCB = 9 * Z_External, where Z_PCB is the Large impedance located on the printed circuit board, and Z_External is the small impedances of the cable and the oscilloscope scope input.

Return to EE 420L Labs...