Lab 1 – Review of Basic RC Circuits

EE 420L Analog IC

Lab date: 1/23/18 Due: 1/30/19

By David Santiago – Email: santid4@unlv.nevada.edu

Last Edited on 2/01/19 at 10:07am using Word

Lab description: In this lab, we will be simulating circuits from the CMOS – 3^rd Edition Textbook and verifying the theoretical circuits with experimental measurements.

---------------------------------------------------------------------------

Circuit 1: Fig 1.21 (Page 18)

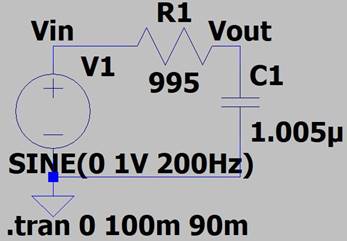
LTSpice:

On The BreadBoard:

R1: 995Ω, C1: 1.005uF

Theoretical Hand Calculations:

Z_C1 = -j / (2πf * C1) = -j / [2π (200Hz) * (1.005uF) ]

= -j791.82Ω

Vout = Vin * (Z_C1) / ( R1 + Z_C1)

= 1V * (-j791.82) / [995 + (-j791.82Ω) ]

|Vout|= /

= 0.623 Volts Theoretically

Phase = tan^-1(-791.82 / 0) - tan^-1(-791.82 / 995)

= (-90)˚ - (-38.5)˚

= -51.5˚ Theoretically

CMOS Book’s Simulation:

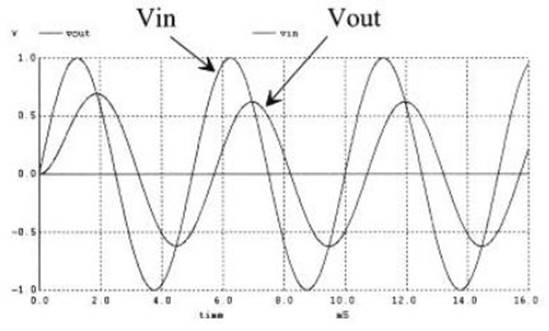
LTSpice Simulation:

LTSpice Values:

Vout = 0.617 Volts

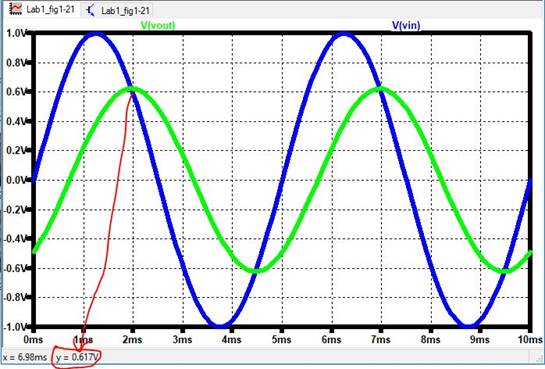
Experimental Oscilloscope Waveforms:

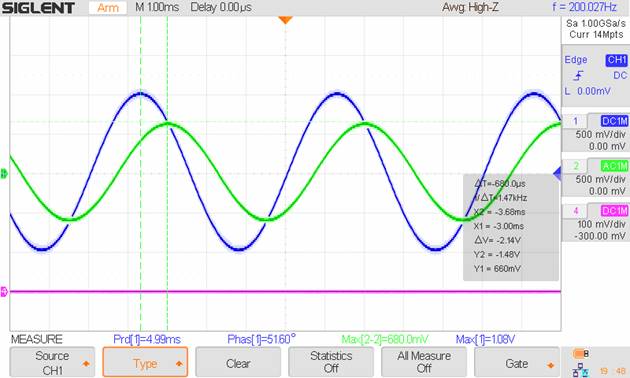
Experimental Values:

Vin (BLUE) = 1.08V, Vout (GREEN) = 0.680V, Phase = -51.6˚

Observations & Analysis:

Comparing the theoretical values from both LTSpice and my hand calculations to the experimental values from the breadboard, both experimental and theoretical values seem to agree with each other.

Calculating the percent error of Vout and phase using : [ (Theo – Exp) / Theo ] * 100%, we have:

Vout % Error = [ (623 – 680) / 623 ] * 100% = 9.1% Error

Phase % Error = [ (51.5 – 51.6) / 51.5 ] * 100% = 0.2% Error

-Here we can see that our voltage output is off by around 10%, and this can be due to one more thing that hasn’t been taken accout of, and that is the Internal Resistance of the power supply, and since we are dealing with low voltages, the small resitance inside the supply can affect our results. Adding a small resistance at the positive supply terminal in our hand calcs will provide us with a better percent error.

-Also, even though the power supply says it is outputting 1 Volt, experimentally we are getting to 1.1 Volts, which is theoretically 10% higher than our 1 Volt supply, which sounds a lot more responsible for the big error.

--------------------------------------------------------------------------------------------

Circuit 2: Fig 1.22 (Page 19)

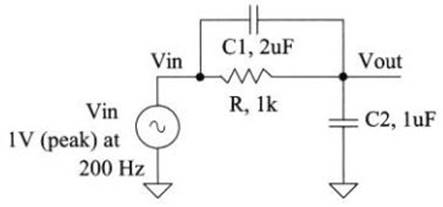
LTSpice:

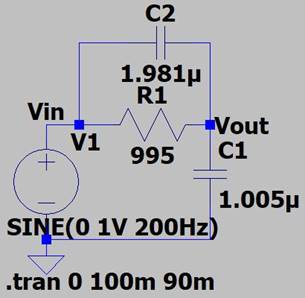
On The BreadBoard:

R1: 995Ω, C1: 1.005uF, C2: 1.981uF

Theoretical Hand Calculations:

Z_C1 = -j791.82Ω (From Circuit 1)

Z_C2 = -j / (2πf * C2) = -j / [2π (200Hz) * (1.981uF) ]

= -j401.7Ω

Z_R1||C2 = (R1 * Z_C2) / (R1 + Z_C2) = [ 995 * (-j401.7) ] / [ 995 + (-j401.7) ]

= 139.45 – j345.4 Ω

Vout = Vin * (Z_C1) / ( Z_R1||C2 + Z_C1)

= 1V * (-j791.82) / [(139.45 – j345.4) + (-j791.82) ]

= 0.686 – j401.7Ω

|Vout|=

= 0.691 Volts Theoretically

Phase = tan^-1(-0.084/0.686)

= -6.98˚ Theoretically

LTSpice Simulation:

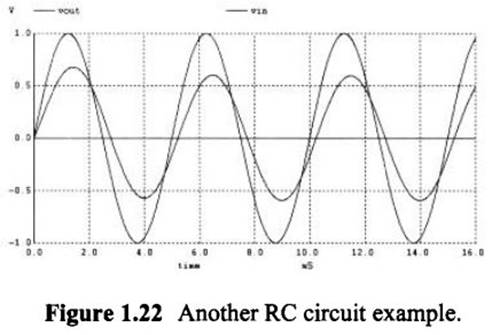
LTSpice Simulation:

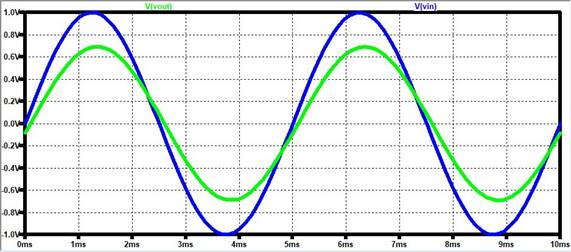
LTSpice Values:

Vout = 0.689 Volts

Experimental Oscilloscope Waveforms:

Experimental Values:

Vin (BLUE) = 1.10V, Vout (GREEN) = 0.80V, Phase = -6.58˚

Observations & Analysis:

Before we begin to evaluate the results:

% Error = [ (Theo – Exp) / Theo ] * 100%

Vout %Error = [ (691 – 800) / 691 ] * 100% = 15.8% Error

Phase % Error = [ (6.98 – 6.58) / 6.98 ] * 100% = 5.7% Error

-From the values, we have about a 15% error with our voltage, and this is most likely the result from having a non-ideal battery source and how the source is about 10% higher than the theoretical value. There could be a higher parallel capacitance with the resistor to where all of the AC current goes through the capacitor and can create that higher voltage potential at Vout.

Our experimental phase shift is also off by a short margin, however, it is close to the theoretical value and can be an -acceted value.

-------------------------------------------------------------------------------

Circuit 3: Fig 1.24 (Page 21) w/Book Output

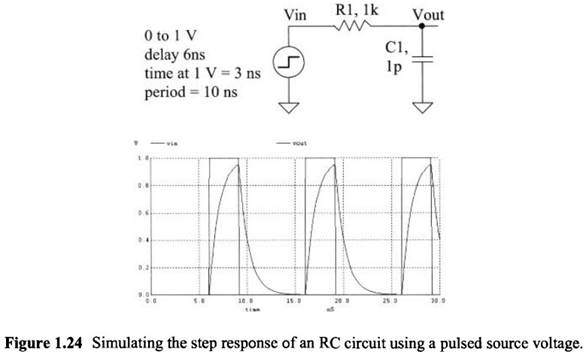
NOTE : Changed 1pF capacitor with 1uF capacitor

LTSpice:

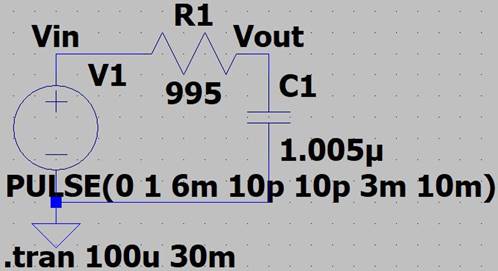
On the Breadboard:

R1 = 995Ω, C1 = 1.005uF

Theoretical Hand Calculations:

RC Time Constant: T = R*C = 995 *(1.005u) ≈ 1ms

Duty Cycle of Square wave = 30% of 1/100Hz = 3ms

Charging Formula: Vout = Vin * (1 – )

Vout = 1V * (1 – e^(-3m/1m))

Vout = 0.95V Theoretically

LTSpice Simulation:

LTSpice Values:

Vout = 0.95 Volts

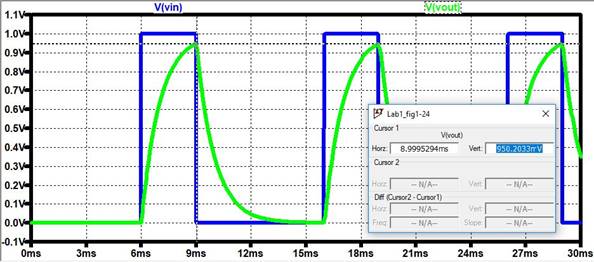
Experimental Oscilloscope Waveforms:

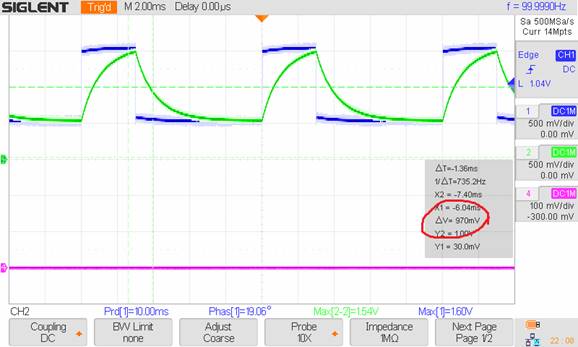
Experimental Values:

Vin (BLUE) = 1V, Vout (GREEN) = 0.97V

Vout = .97V Experimentally

Observations & Analysis:

% Error = [ (Theo – Exp) / Theo ] * 100%

Vout % Error = [ ( .95 - .97) / .95 ]*100% = 2.1% Error

From looking at our simple circuit, we can see that the capacitor is charging and that both the theoretical and experimental values match. The error could have been that the charger does not fully discharge at the end and so we charge from somewhere a bit over .01 Volts and get a small error that we can live with.

-----------------------------------------------------------------------------------------------

Circuit 4: Fig 1.23 (Page 20)

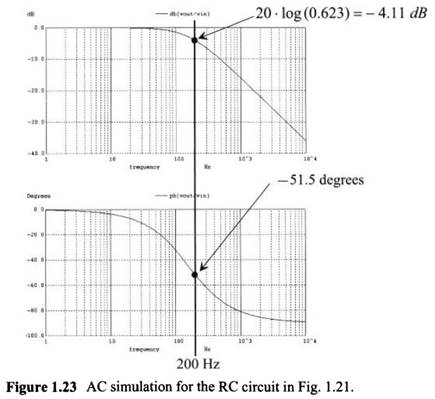
Respective Circuit:

LTSpice:

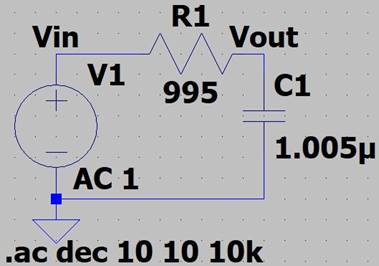
R1 = 995Ω, C1 = 1.005uF

Theoretical Hand Calculations:

Voltage Divider:

Vout = Vin * [1/(j2πf*C1)] / [R1 + 1/(j2πf*C1)]

Vout/Vin = 1 / ( 1 + j2πf*C1*R1) //Multiplied Top and bottom by j2πfC1

|Vout/Vin| = 1 /

20Log|Vout/Vin| = - 20Log

Phase = tan^-1(0/1) - tan^-1[(/1)]

=- tan^-1[(/1)]

f3db = 1/( 2π*C1*R1)

= 1/ (2π*1.005u*995)

f3db = 159.15Hz (Point where we have 3db and -45˚ Phase shift)

LTSpice Simulation:

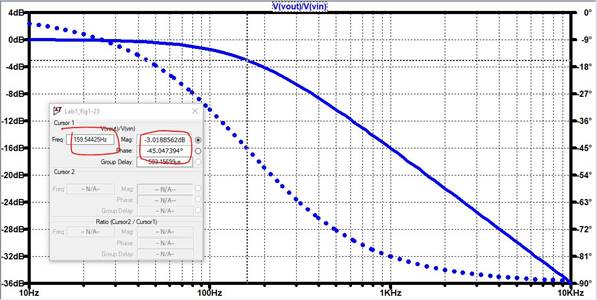
f3db = 159.54Hz

Experimental Part:

For this, we take the Oscilloscope’s calculated Maximum voltages for both Vin and Vout and take the magnitude, and we read the oscilloscope’s calculated phase shift.

Vin (BLUE), Vout (GREEN)

10Hz: Vout/Vin = 1.08V/1.1V, Mag = -0.16db Phase = -6.61˚

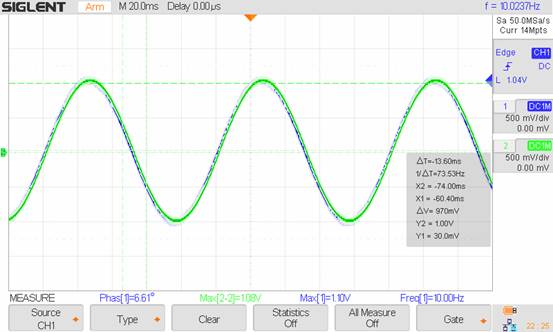
100Hz: Vout/Vin = .92V/1.1V, Mag = -1.55db, Phase = -30.64˚

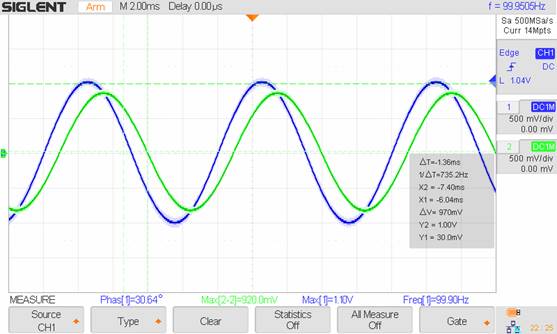
1kHz: Vout/Vin = 0.24V/1.06V, Mag = -12.9db, Phase ≈ -90˚

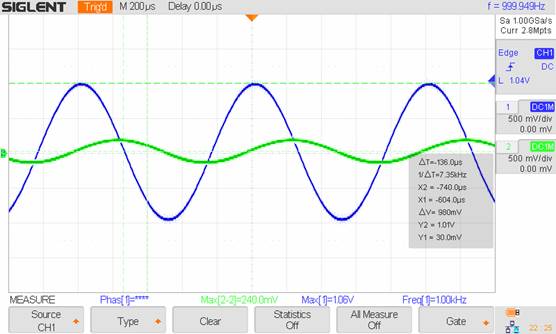
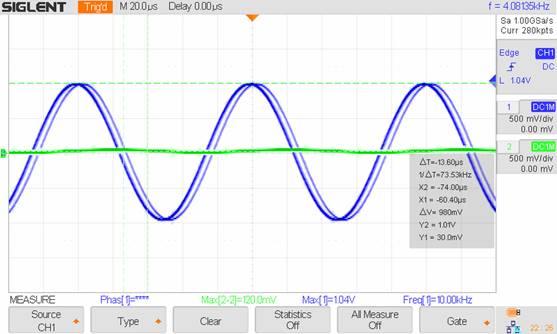
10kHz: Vout/Vin = 0.12V/1.04V Mag = -18.76db, Phase ≈90˚

Frequency	Magnitude	Phase
10Hz	-0.16dB	-6.61
100Hz	-1.55dB	-30.64
1kHz	-12.9dB	≈-90
10kHz	-18.76dB	-90

Observations & Analysis:

From the data, we can assume that both the hand calculations and the experimental values match. Even though there were some long shot data from the experiment, the 3dB frequency is in the general area of 150Hz.

Other things that can be taken account for would be that there is a capacitance in the cable that can cause the 3db frequency to shift. Also, more data points and specifically one at the 3db frequency would prove that the hand calculations are correct.

Furthermore, from the data, we can say that this circuit is for sure a Low Pass filter. For lower frequencies and by observation, we will generally have an accurate frequency pole, however, and in future labs, we will have to deal with parasitic capacitances in high frequency circuits, and these capacitances will cause a problem, however, future testing and teaching from the labs will help students with figuring out how to deal with these problems.

Return to EE 420L Labs...