Lab 4 - EE 420L
Engineering Electronics II
Author:
Matthew Meza
Email:
mezam11@unlv.nevada.edu
February
20, 2015
Op-Amps
II, Gain-Bandwidth Product and Slewing
Click on any picture for its
full size!
Pre-lab work
Lab Description
- Learn and experience how Gain-Bandwidth Product and slewing
affect non-ideal op amps
Lab Data
For the following questions and experiments
assume VCC+ = +5V and VCC- = 0V.
Part
1:
- Estimate,
using the datasheet, the bandwidths for op-amp topologies having gains
of 1, 5, and 10.
- GBW of the
LM324 op amp is 1.3MHz
- BW = GBW/|A|
where |A| is the closed loop gain of 1, 5, and 10.
- For a gain of
1, the BW = GBW/1 = 1.3 MHz
- For a gain of
5, the BW = GBW/5 = 260 KHz
- For a gain of
10, the BW = GBW/10 = 130 KHz
- These BW are
the same for both the non-inverting and inverting topology
Part 2:
| Non-Inverting Topology |
Gain
|
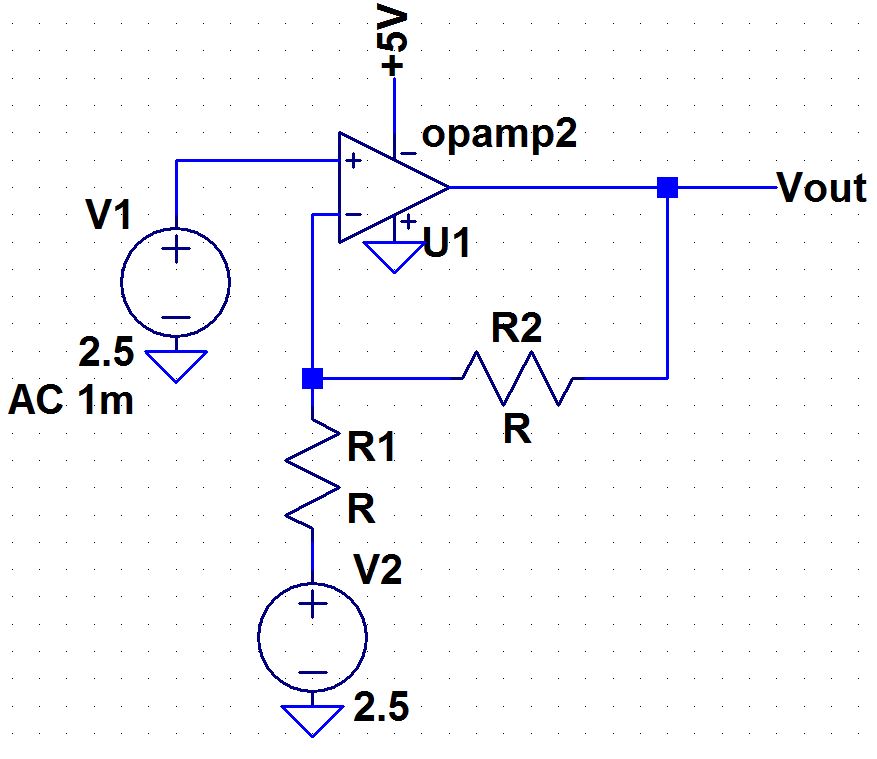 |
R1 is set to be 10K
For a gain of 1, R2 is set to be 0
For a gain of 5, R2 is set to be 40k
For a gain of 10, R2 is set to be 90k
|
Experimental Results
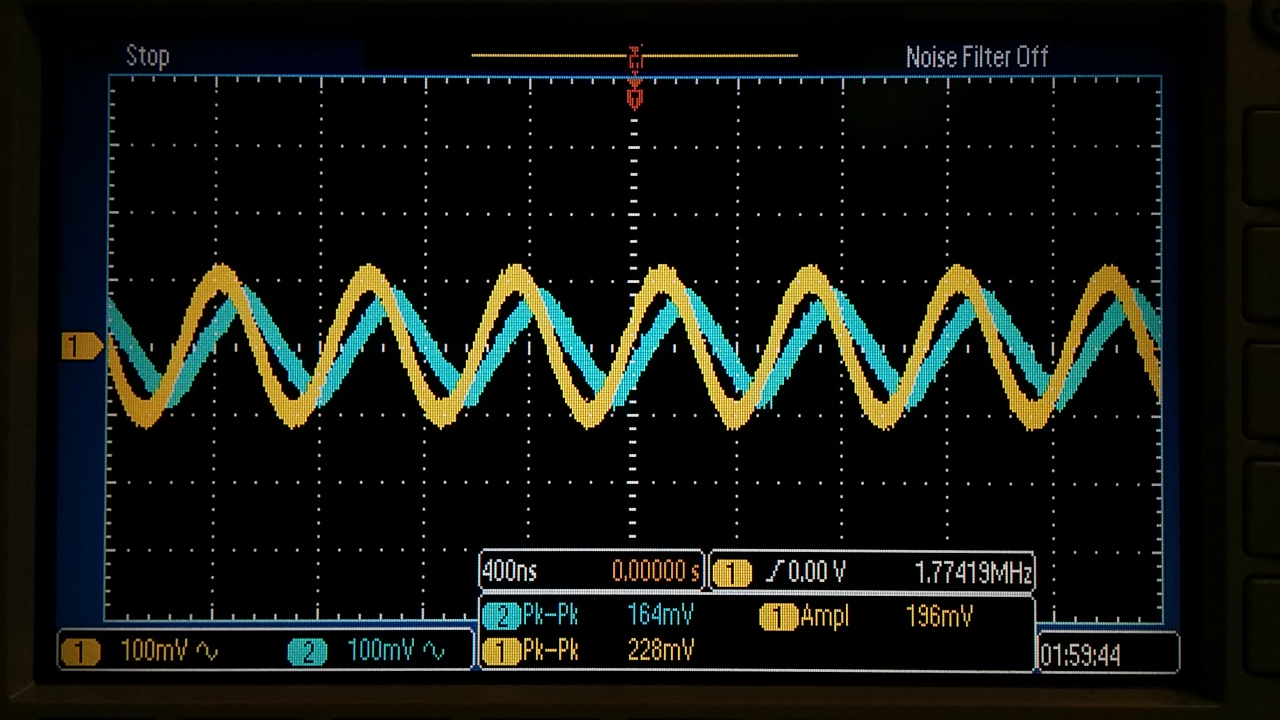
3dB @ 1.77MHz
|
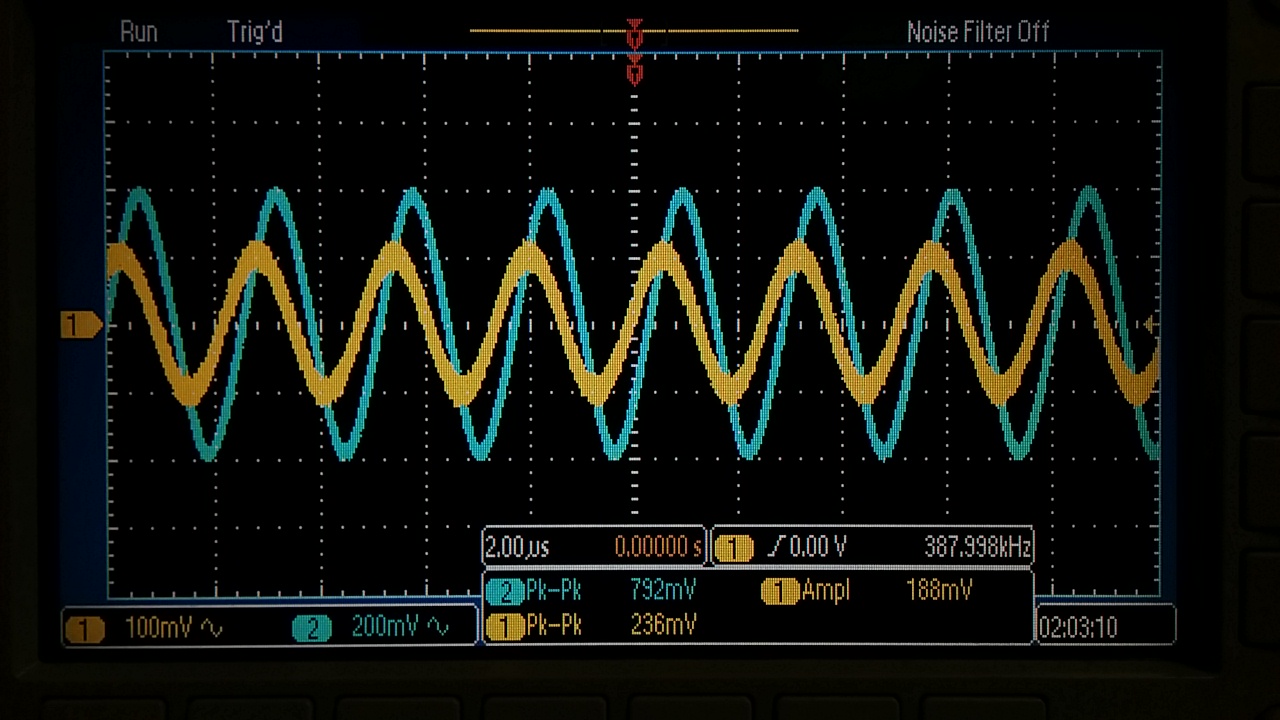
3dB @ 388 KHz
|

3db @ 203.5KHz
|
At a gain of 1, 3dB = 1.77 MHz
At a gain of 5, 3dB = 388 KHz
At a gain of 10, 3dB = 203.5KHz
|
Conclusion:
The op amp demonstrates a bandwith much higher that what was expected
from the datasheet and from what was calculated in Part 1. One can
assume that there is some variation in manufacturing of Op-Amps. Most
of the time, the GBP from a datasheet is higher than the actual GBP due
to the different testing done by the manufacturer but in our case the
experience was opposite.
Part
3:
| Inverting Topology |
Gain
|
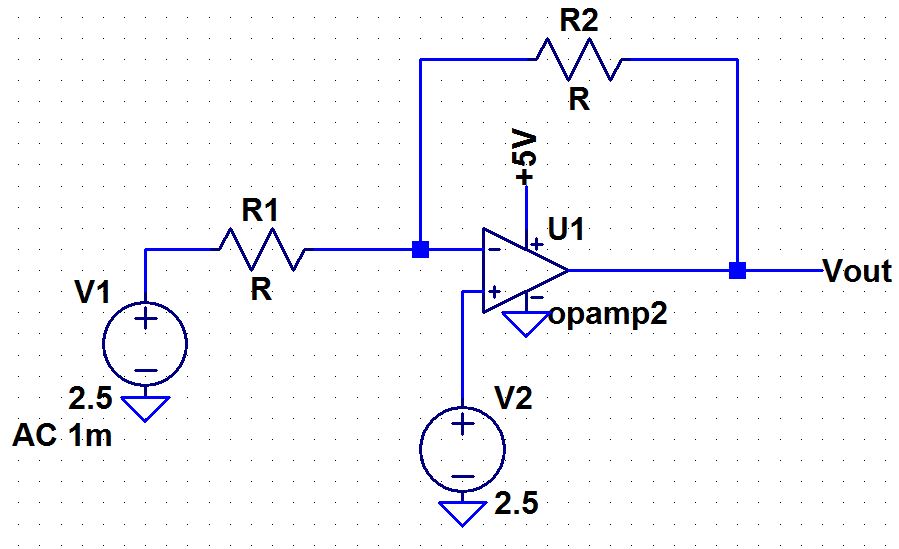
|
R1 is set to be 10K
For a gain of 1, R2 is set to be 10K
For a gain of 5, R2 is set to be 50k
For a gain of 10, R2 is set to be 100k
|
Experimental Results

3dB @ 1.26MHz
|

3dB @ 348 KHz
|
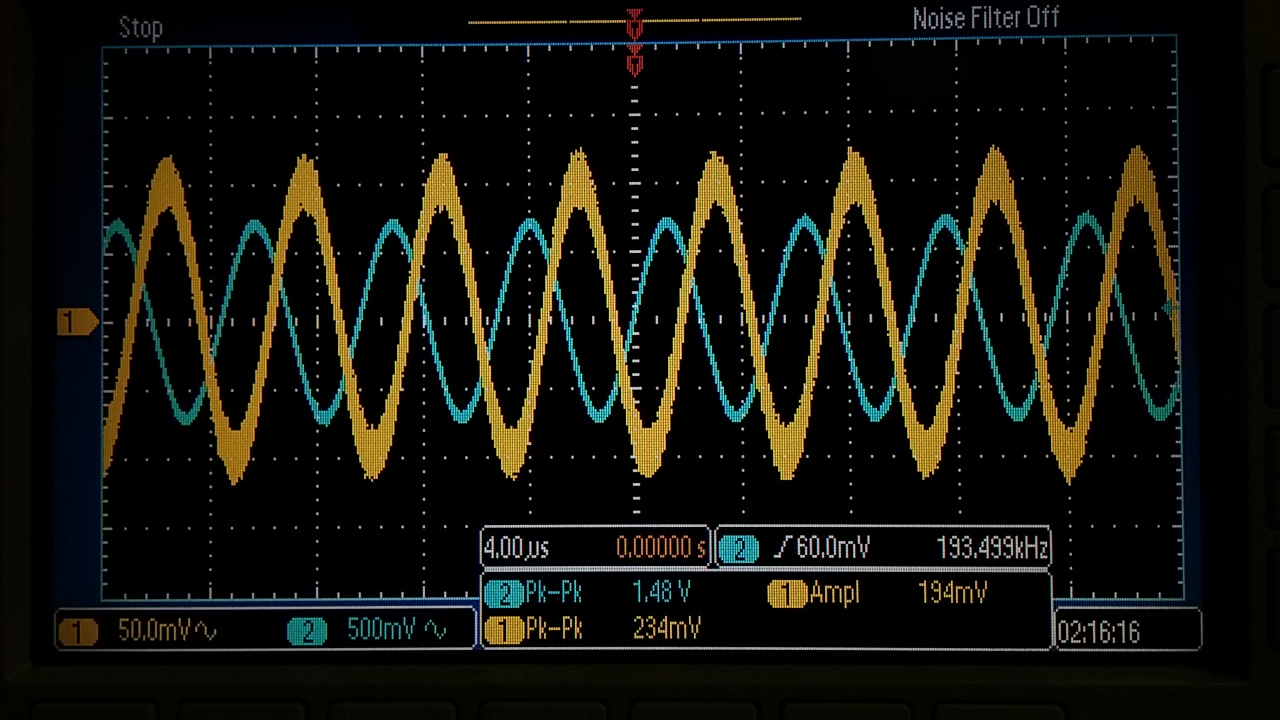
3db @ 193KHz
|
At a gain of 1, 3dB = 1.265 MHz
At a gain of 5, 3dB = 348.5 KHz
At a gain of 10, 3dB = 193.5KHz
|
Conclusion:
The op amp demonstrates a bandwith much more reasonable than the
previous experiment. 1.265 MHz is much more accurate to that of what
was expected
from the datasheet. Although, for the different gain values, we see
still see higher values that what we calculated in Part 1. Agian, one
can assume that
there is some variation in manufacturing of Op-Amps. Most of the time,
the GBP from a
datasheet is higher than the actual GBP due to the different
testing done by the manufacturer.
Part 4:
- Design two circuits
for measuring the slew-rate of the LM324. One circuit should use a
pulse input while the other should use a sinewave input.
Often times, the slew rate
issues are thought to be caused solely by high frequencies.
This idea is partially incorrect. Slew rate issues
occur when both an output's
signal is very large (high voltage) and changes quickly (high
frequency. If one outputs a voltage of 10V, slew rate problems
will occur at much lower frequencies. If one outputs a small voltage of
10mV, then slew rate issues occur at migh higher frequencies.
For
example in the 'Sinusoidal Slew Rate' shown below, the output must swing 2.56
volts (Pk-Pk) at a frequency of 202KHz. We can estimate the
"Sinusoidal
Slew Rate" to be the voltage of the input divided by the period of the
output (6.16/5) = 1.23 V/uS. Compared to the datasheet value
of 0.4
V/uS, the slew rate for a sinusoid is much higher. However, looking at the slew
rate of a pulse we can see that the slew rate is estimated to
be
(.704/1.8) = .39 V/uS. This slew rate is much closer to the slew rate found in the
datasheet.

Sinusoidal Slew Rate
|
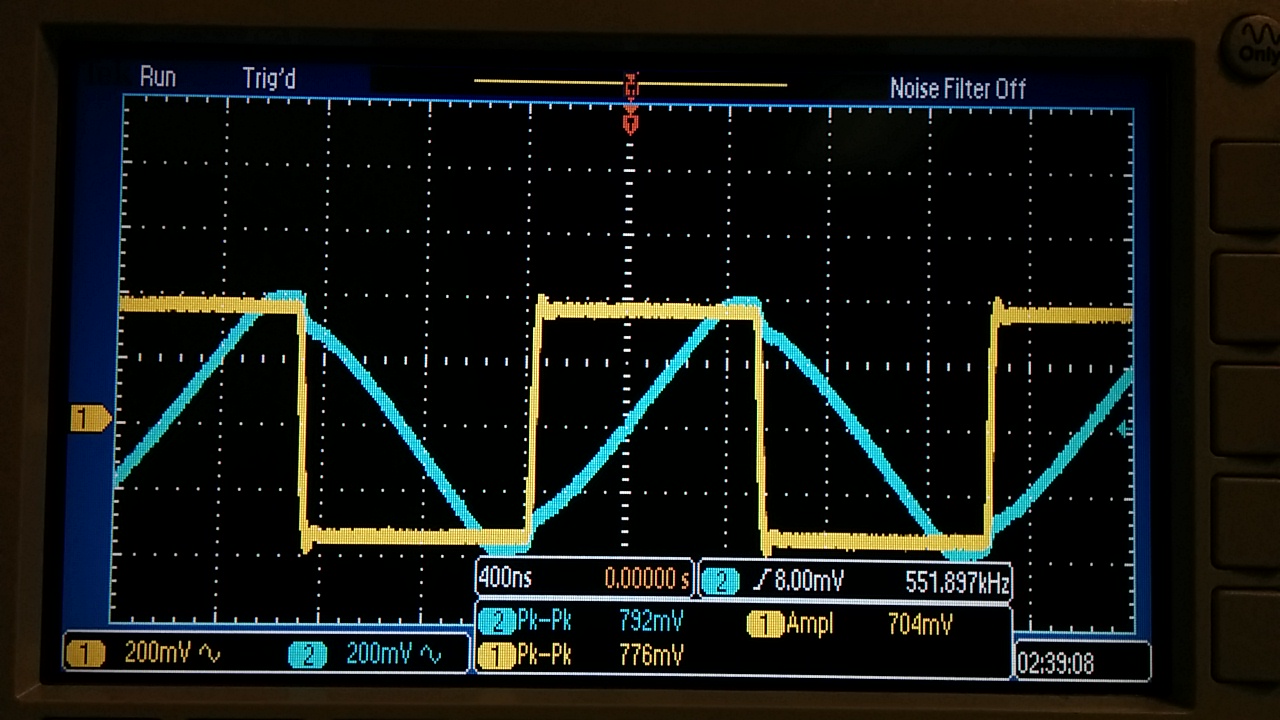
Pulse Slew Rate
|
Return
to EE 420 Labs







