Lab 7 - EE 421L 

Authored by Ricardo Rodriguez

UNLV E-mail: rodrir15@unlv.nevada.edu

November 3, 2021

         

Prelab Work: 

A ring oscillator without the use of arrays/buses
     
A ring oscillator with the use of arrays/buses
       
Symbol and schematic for simulation

     
 Simulation Results

                                        Simulation of the ring oscillator without using initial conditions
                                        Simulation of the ring oscillator using initial conditions (output/input is 0)
  
           
We can add our inital condition by going to Simulations > Convergence Aids > Initial Conditions
   



Now, to create the layout of the ring oscillator
     
 We connect 2 inverters together and then delete the 2nd inverter to copy the remains and make it easier to create 31 stages
     
     
We can then connect our output to our input to create a feedback loop by connecting them to Metal2 by via

       
and then we can connect our pins, but our LVS will fail as the schematic does not have a pin for osc_out, so we have to add it in
       
         


If we LVS again, we will see that it matches and we can run the simulation off of our extraction
   

     
     

     

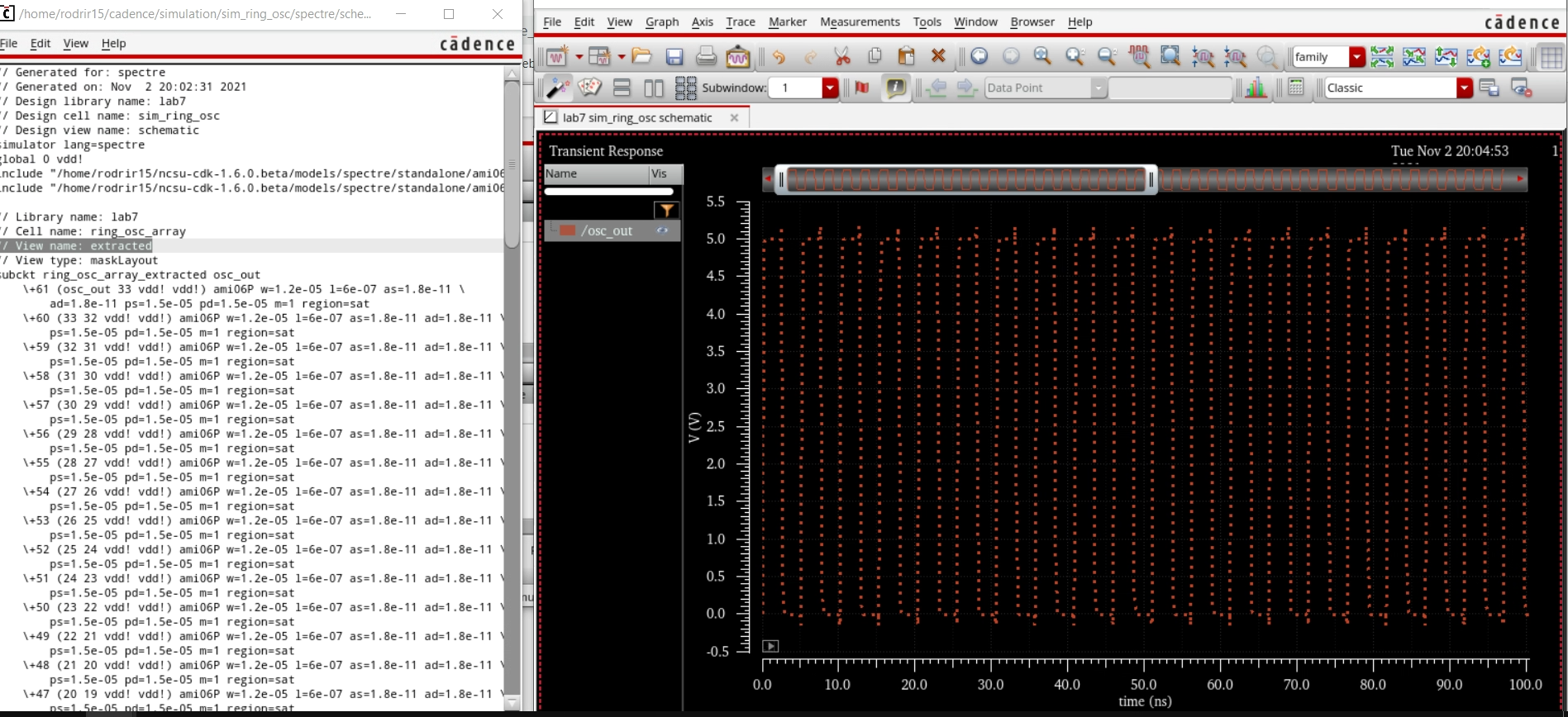
Lab Work:

For the lab we create a 4 bit inverter, an 8 bit inverter, OR, NOR, AND, NAND gates. This is done by the use of buses rather than creating many instances of gates

    4 Bit Inverter: 
Schematic

     
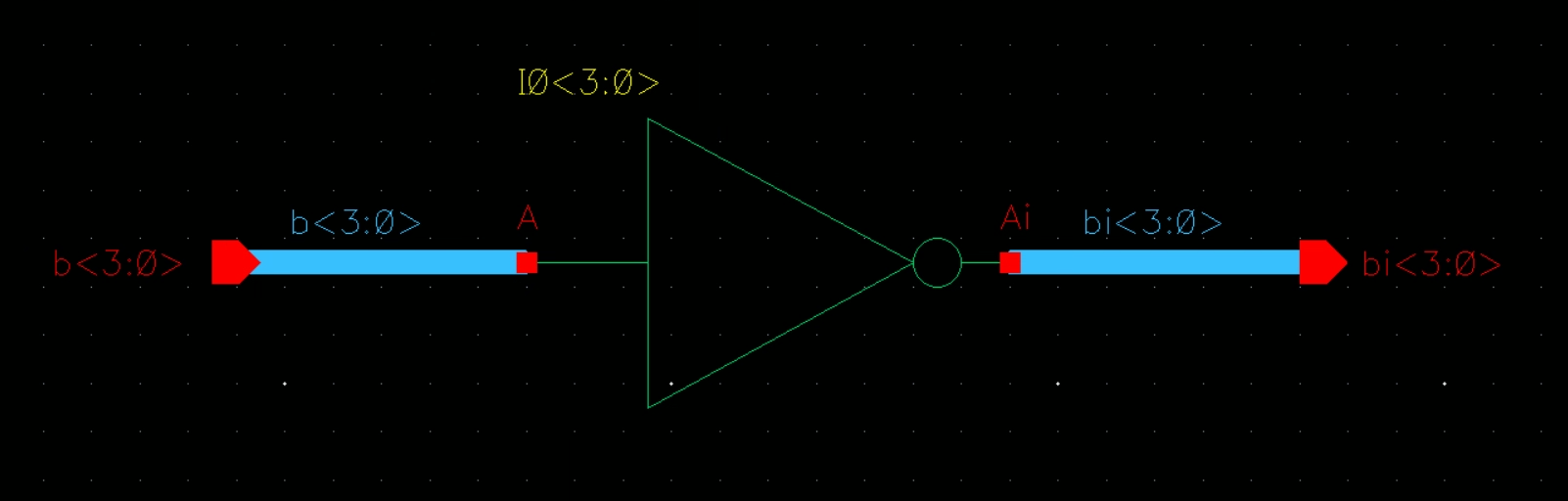
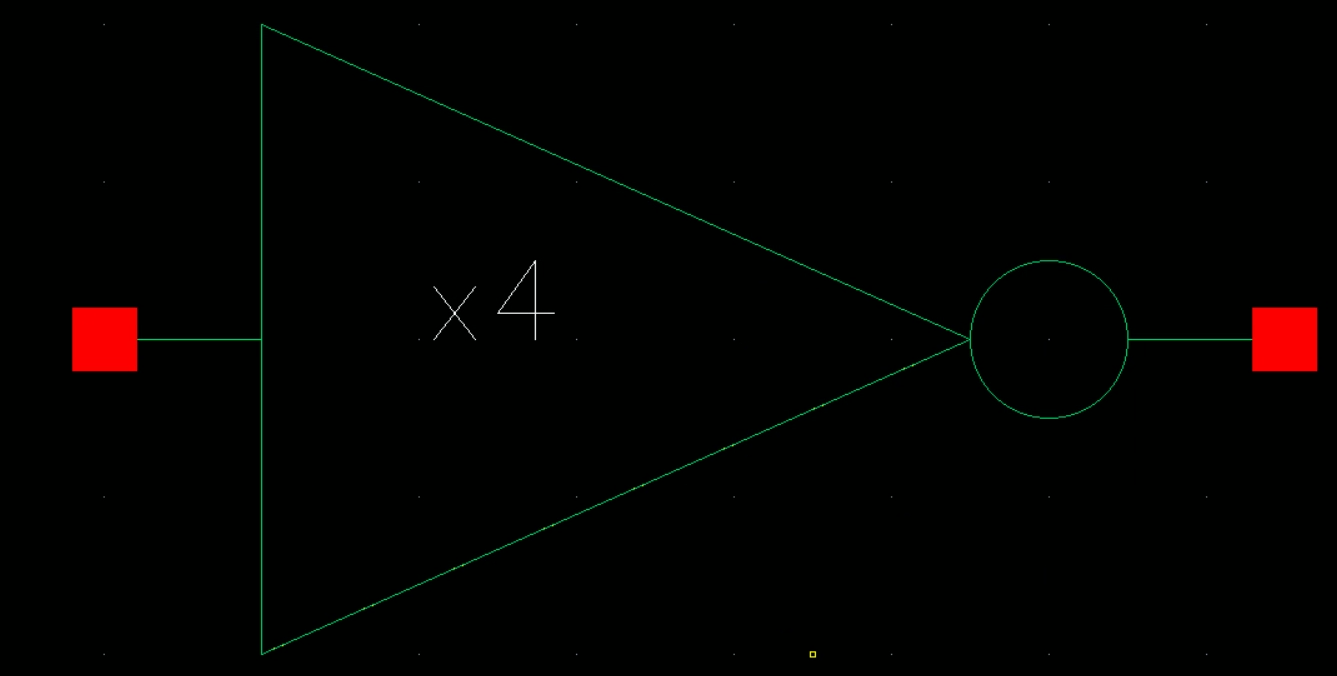
Symbol

       
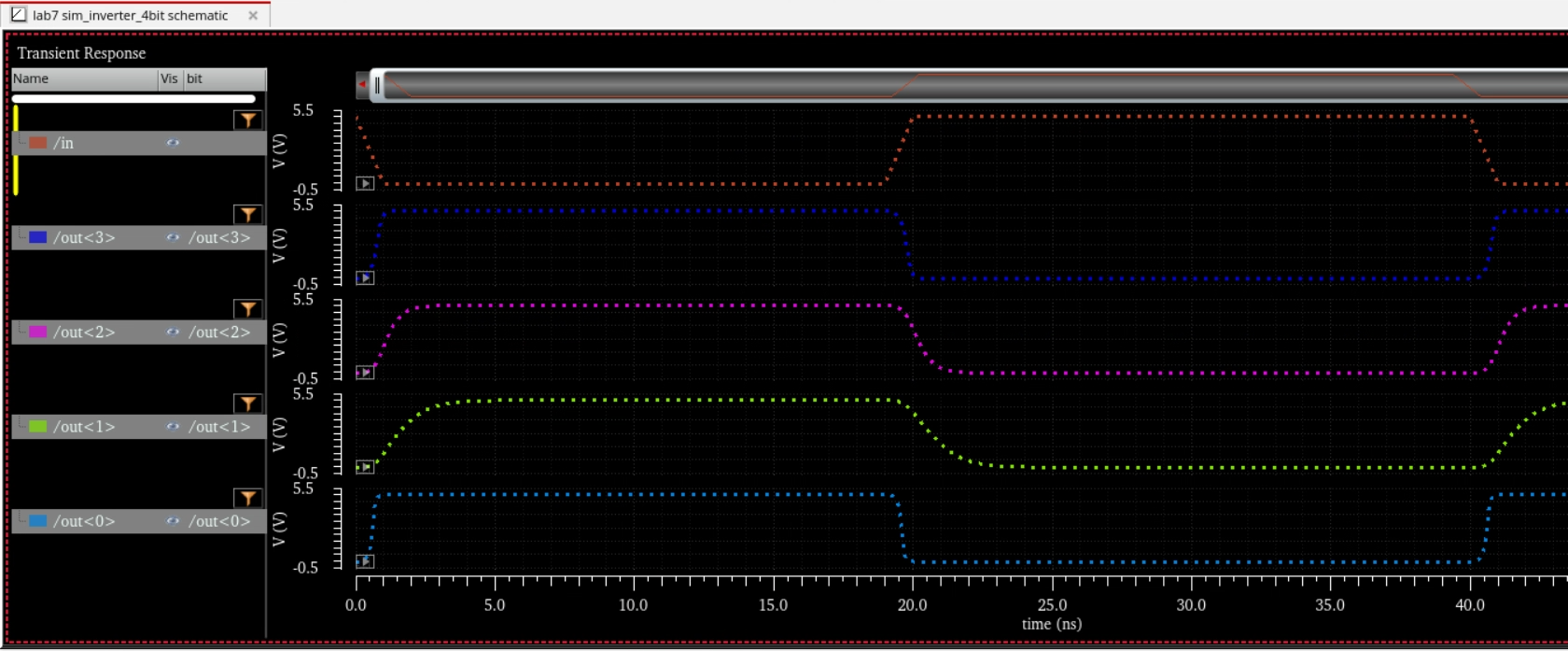
Simulation Schematic and Sims
   


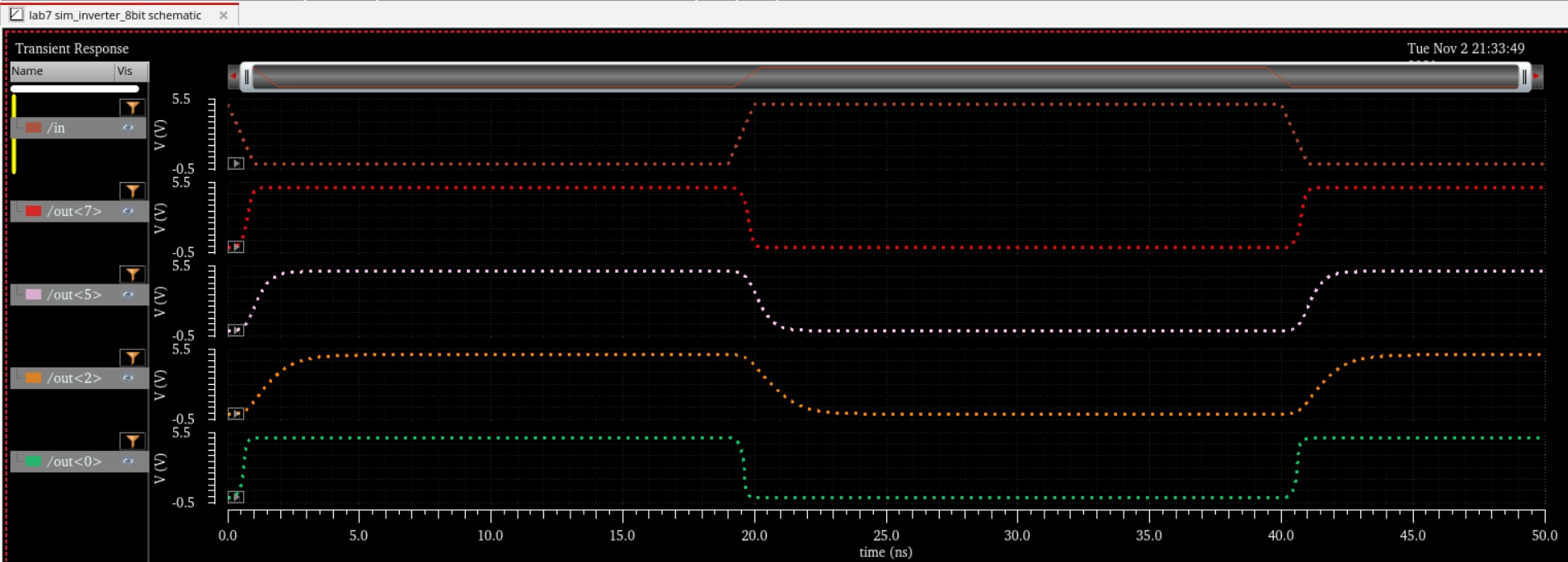
    8 Bit Inverter: 
Schematic

     
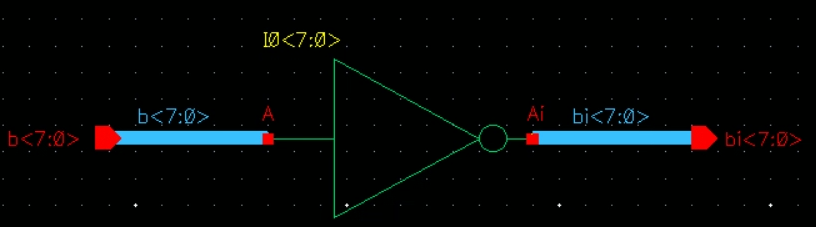
Symbol

       
Simulation Schematic and Sims
     
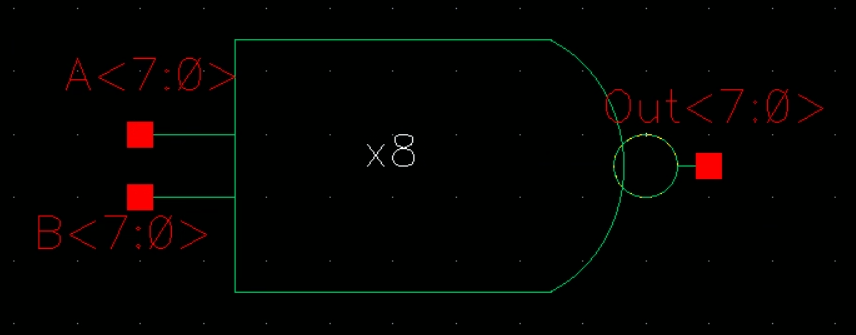
    8 Bit NAND: 
Schematic

     
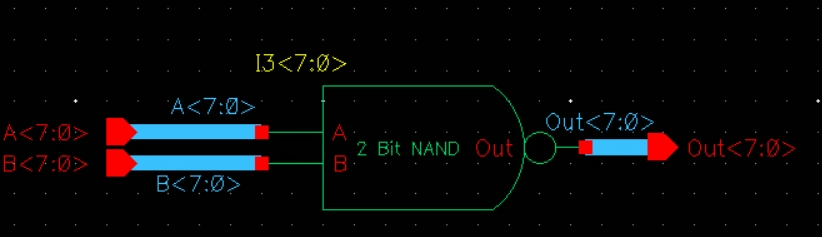
Symbol

       
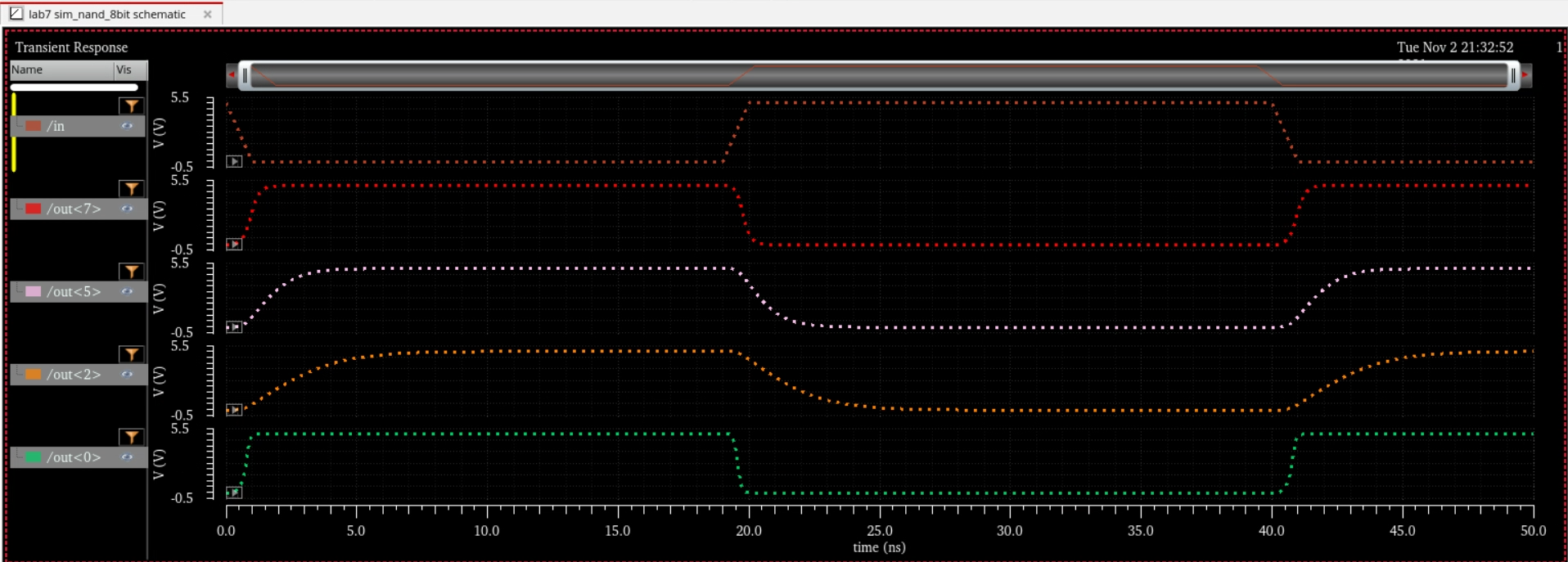
Simulation Schematic and Sims
     

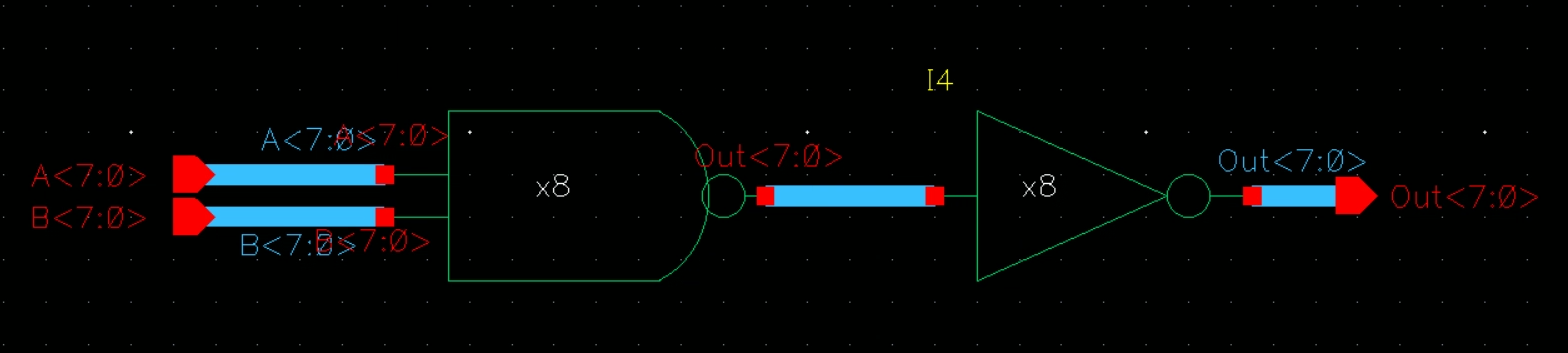
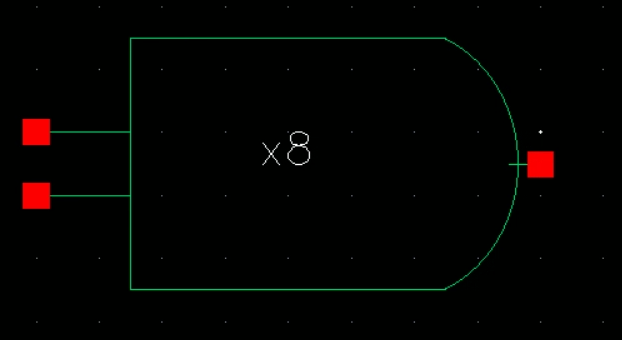
    8 Bit AND: 
Schematic

     
Symbol

       
Simulation Schematic and Sims
     
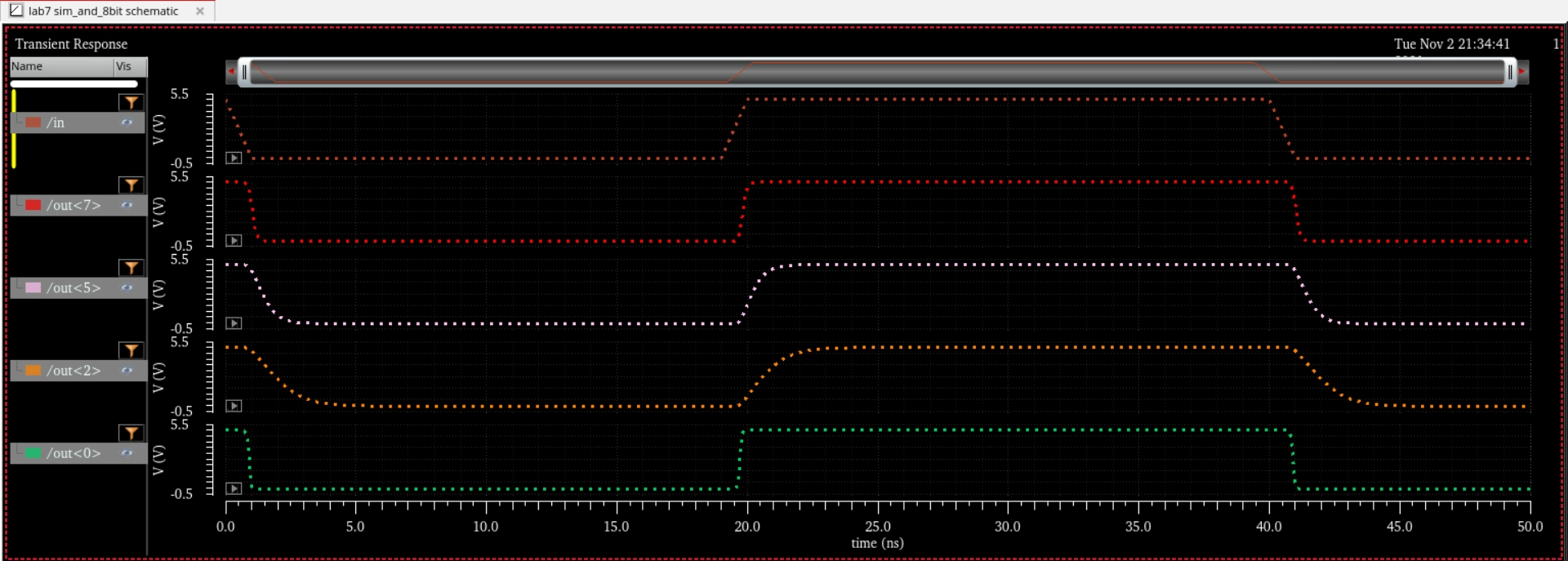
    8 Bit NOR: 
Schematic

     
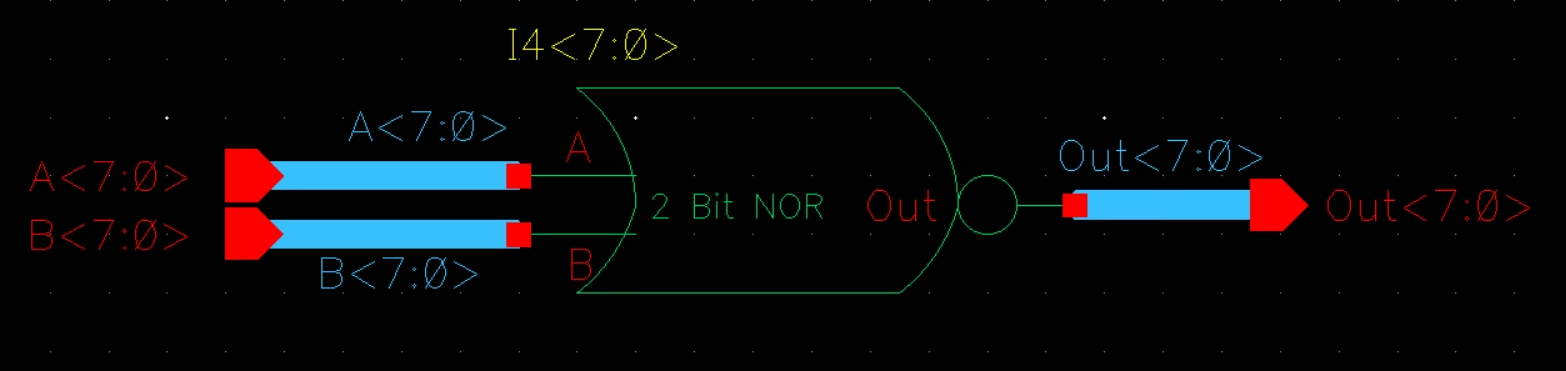
Symbol

       
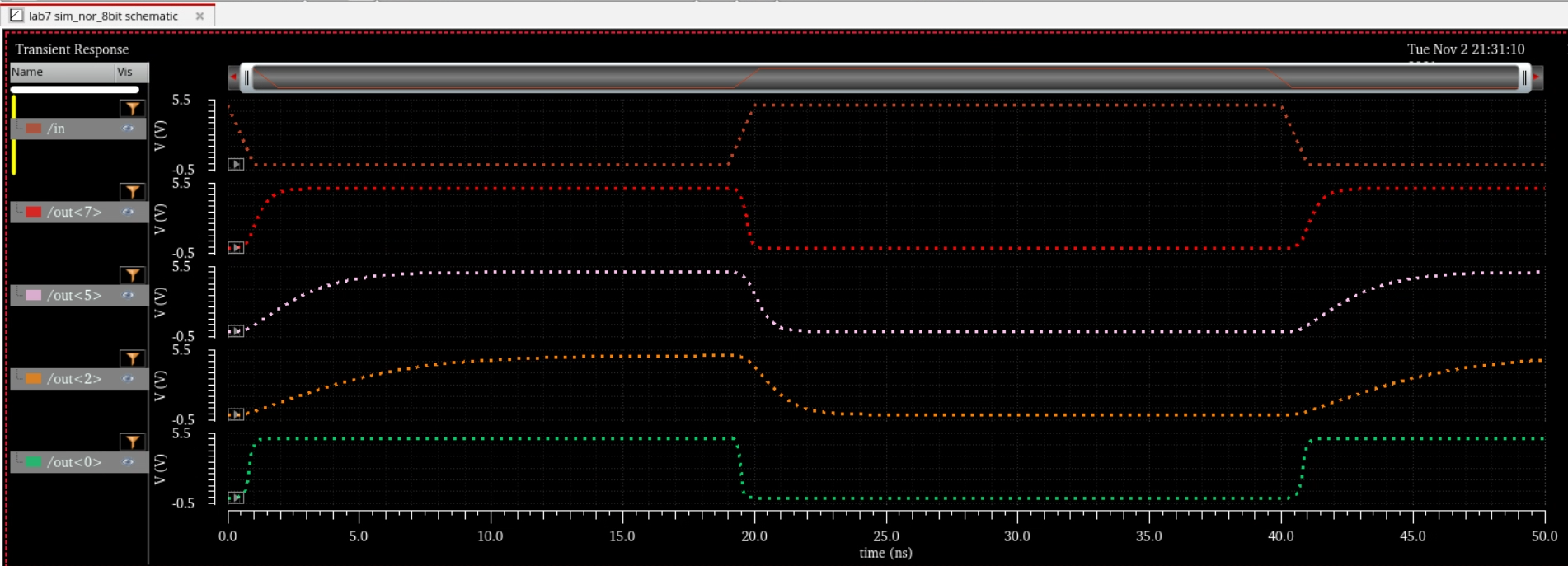
Simulation Schematic and Sims
     
    8 Bit OR: 
Schematic

     
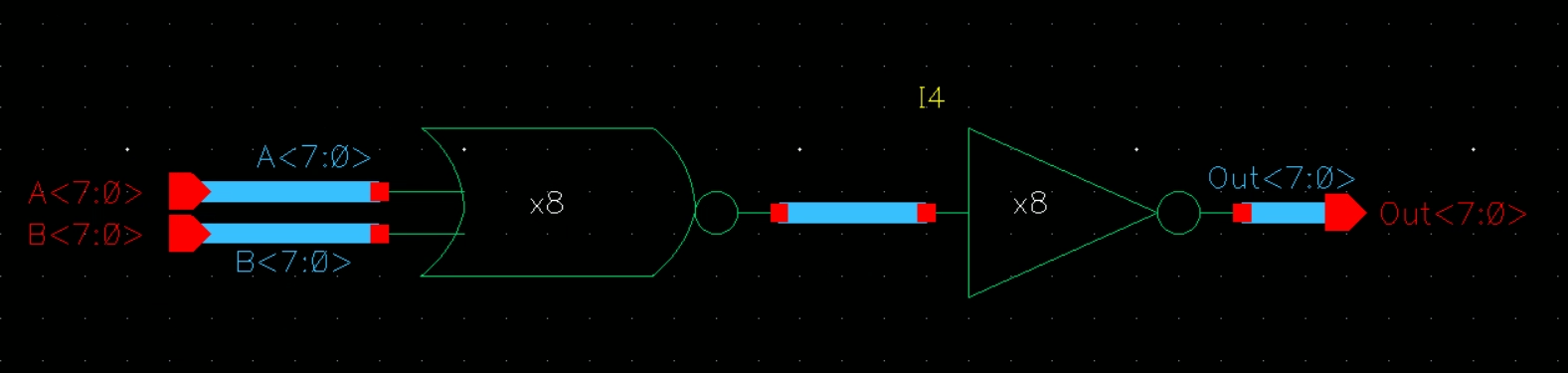
Symbol

       
Simulation Schematic and Sims
     

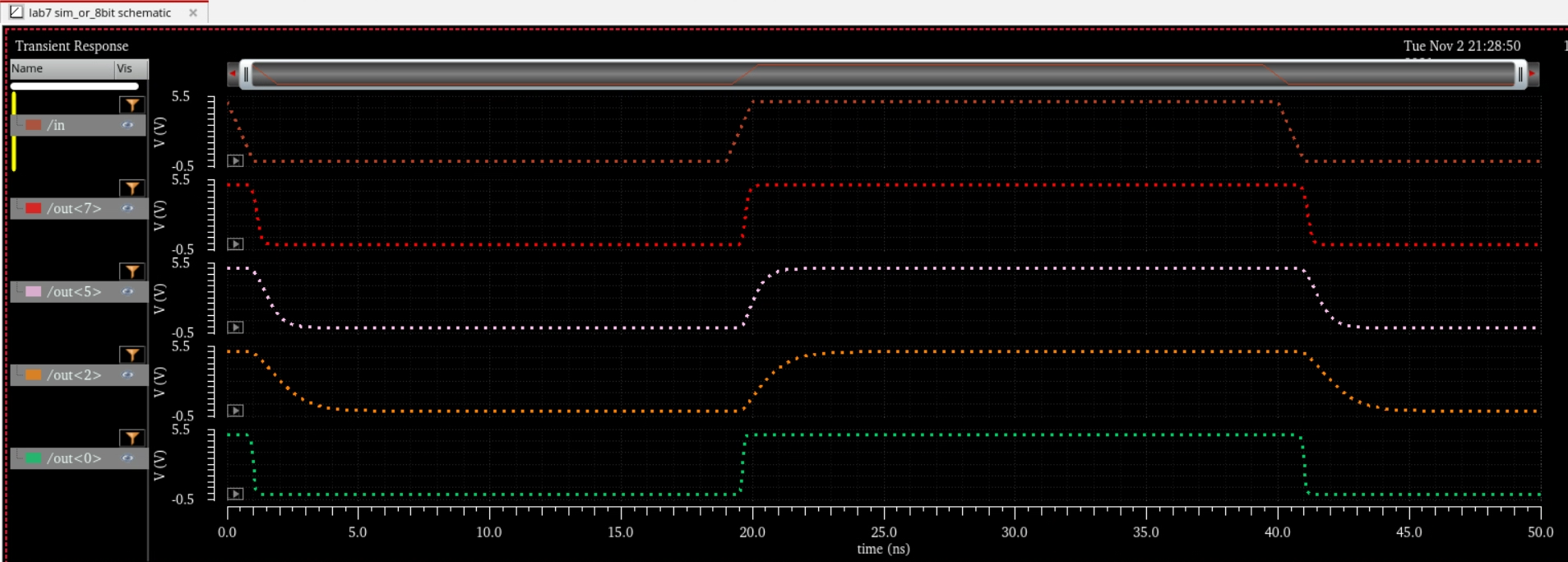
Next, we had to work on a MUX. A MUX allows us to choose an input based off of our selection input. It maintains the equation Z = A*S + B*Si

A DEMUX works in the opposite way. Based on our input, (z in this case) we can choose either A or B based off of our S and Si

Operation of a MUX.

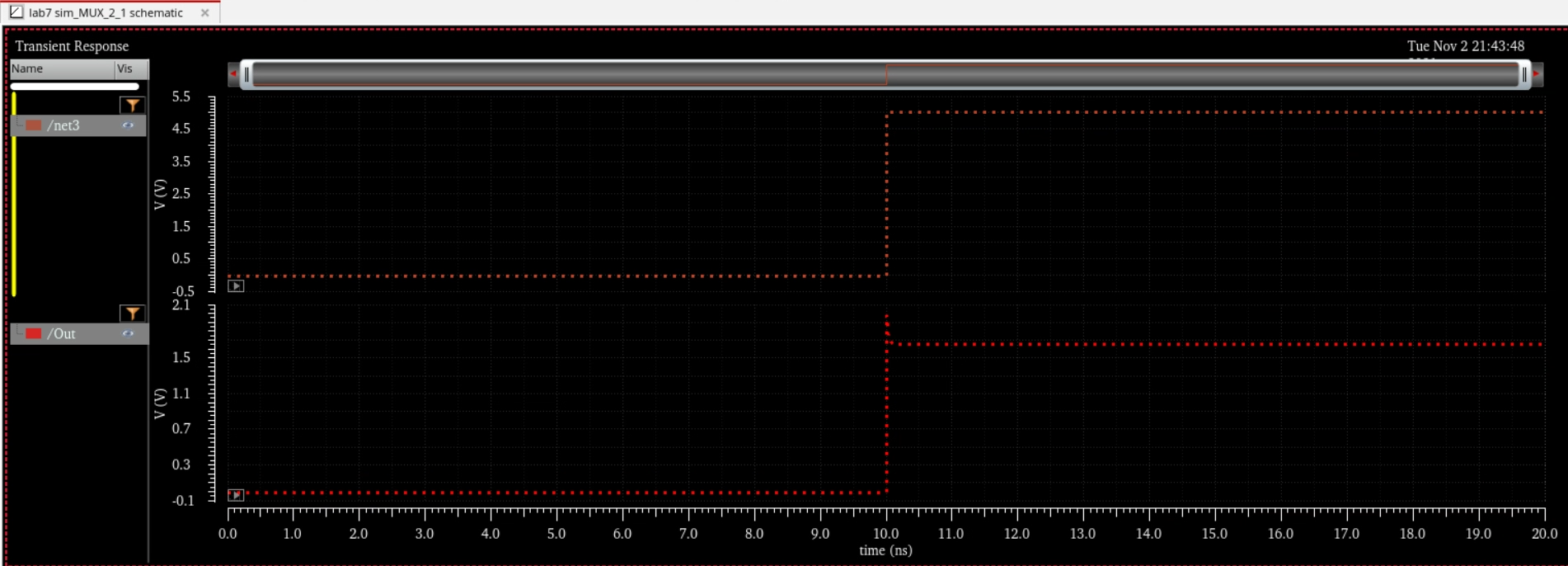
                  Schematic to simulate the MUX                                                                                     Simulation of the MUX

   

Now we create an 8bit MUX like the following

    

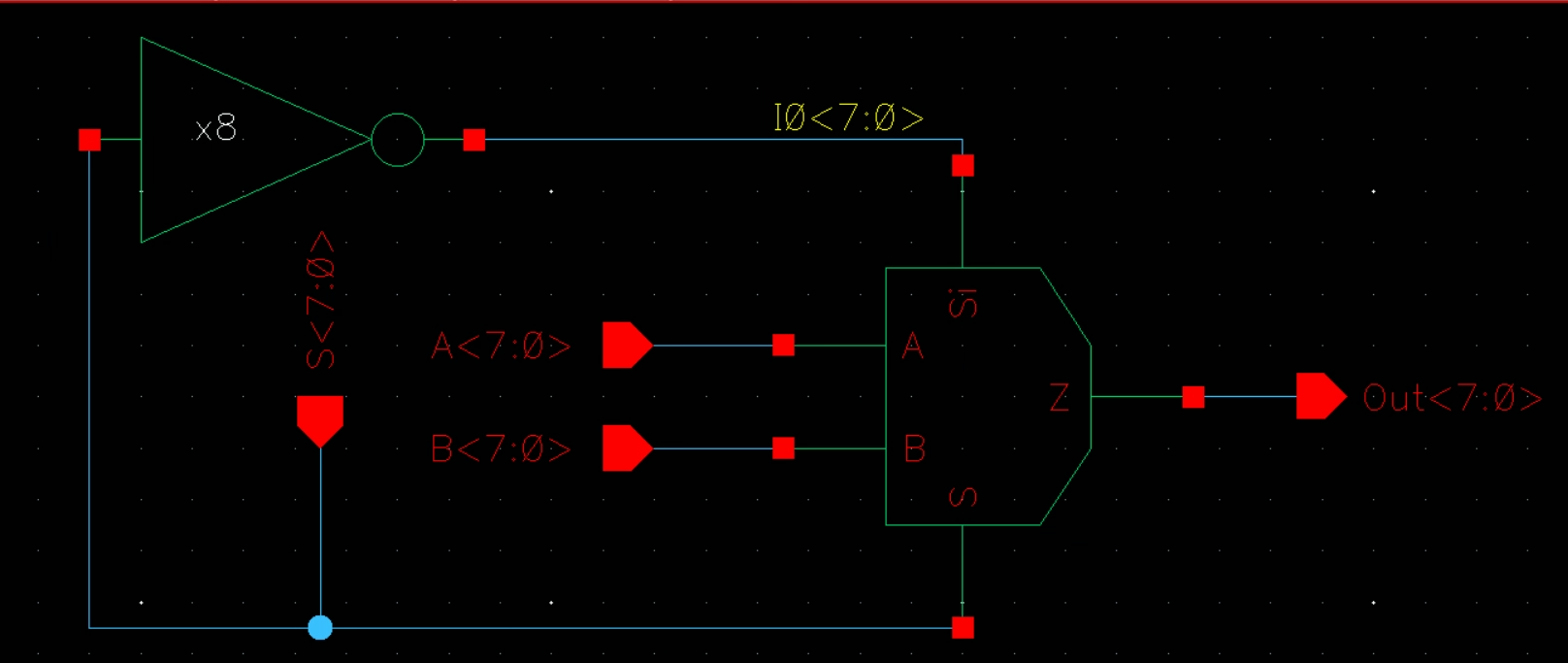
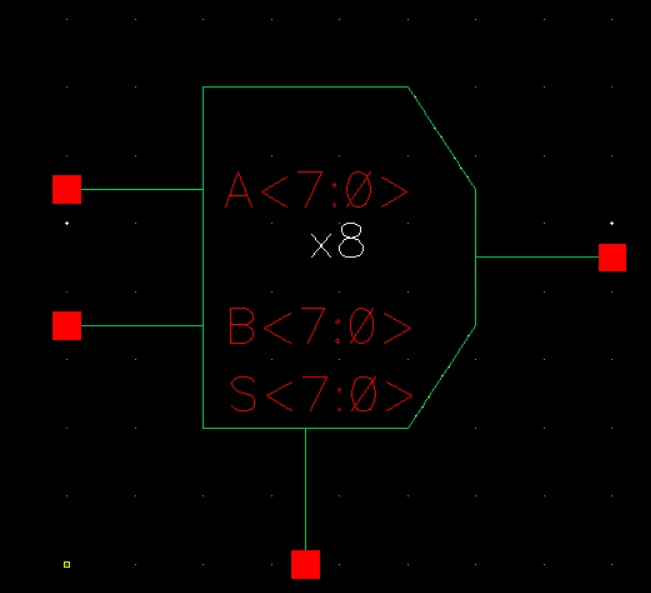
with this symbol   (our Si is built-in)

     

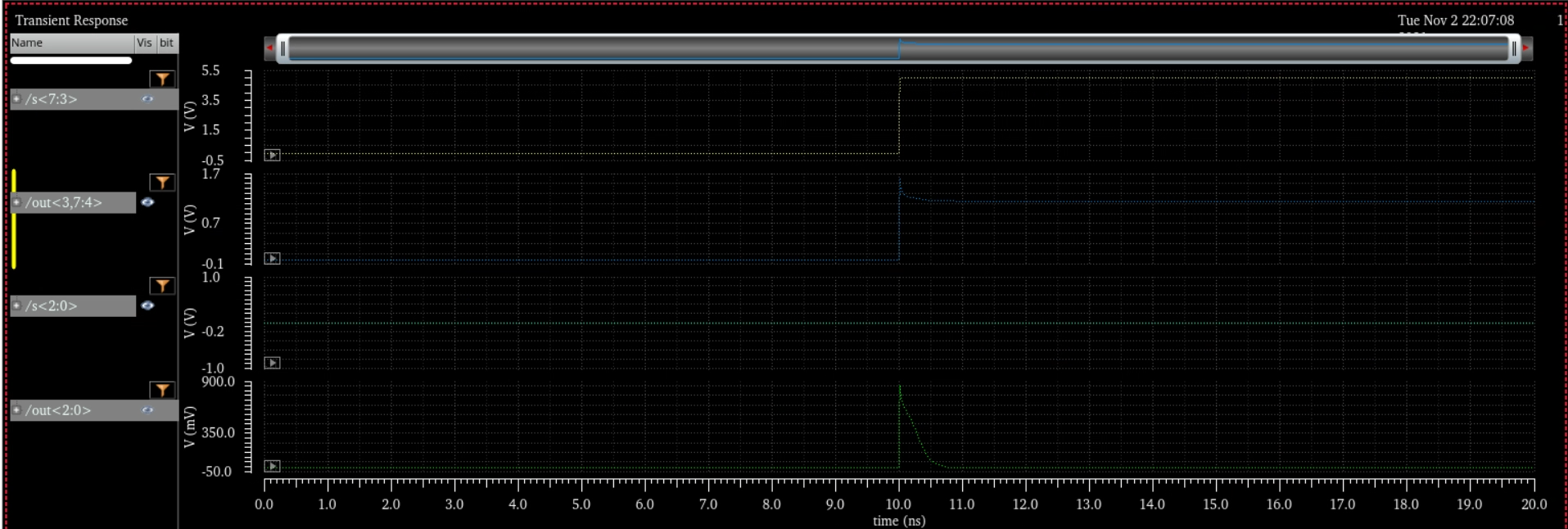
We can simulate our 8 bit mux like this

   

   

        

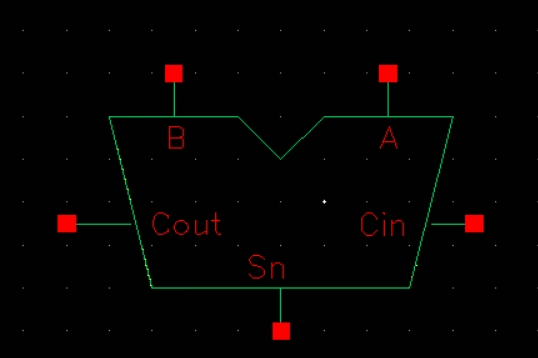
The next part of the lab is to create an 8bit adder. We do this by starting from the beginning

       

                    Schematic for a 1bit adder                                                        Symbol for the full adder

         

     
                                An 8 bit adder using buses and arrays                                                                                Symbol for the 8bit full adder

     

       
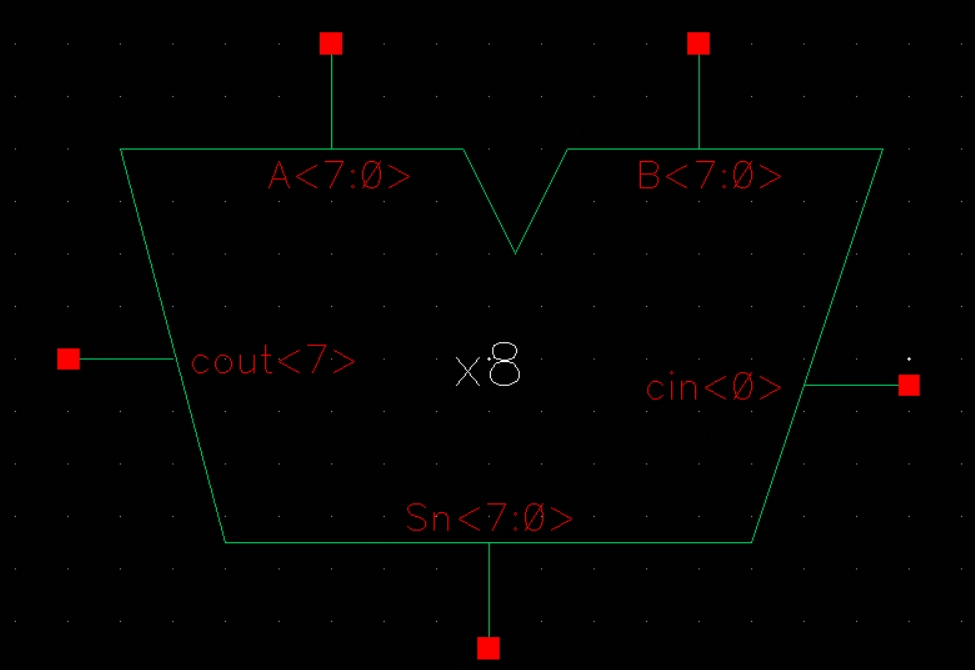
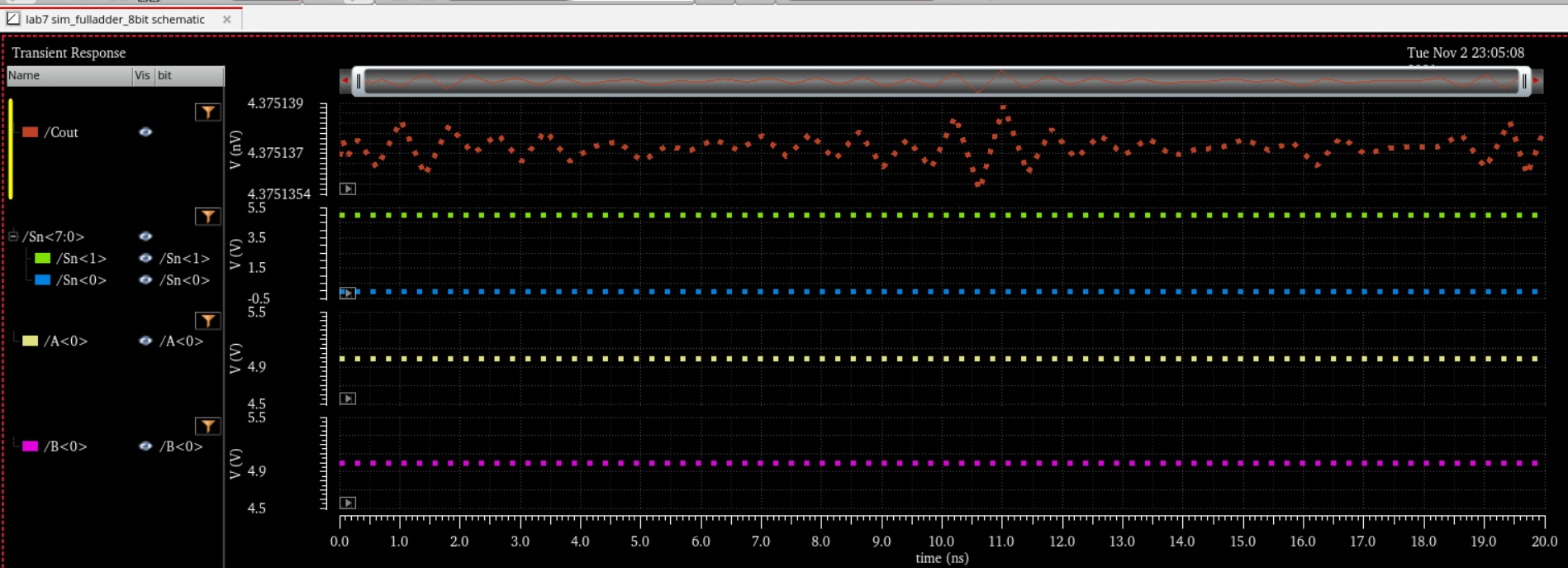
                      Simulating the adder by adding
                        A:00000001 and B:00000001                                                            Our output is Cout:0    Sn:00000010

     


          

Return to my labs

     

Return to student labs