Lab

Lab 6 - EE420L

Authored by Rodolfo Gutierrez

gutie284@unlv.nevada.edu

3/28/2016

Single-stage transistor amplifiers

Below are schematics for NMOS and PMOS source followers amplifiers (also known as common-drain amplifiers).

In your lab report discuss the operation of these circuits.

The source follower circuit works by utalizing the voltage divider equation Vout = Vin Rout / Rout + 1/gm. So the gain in these circuits are dependant on gm and Rout. We can manually pick any value for Rout, however the gm is dependant on the DC biasing, primarily the value for Rin.

Simulate the operation of these amplifiers.

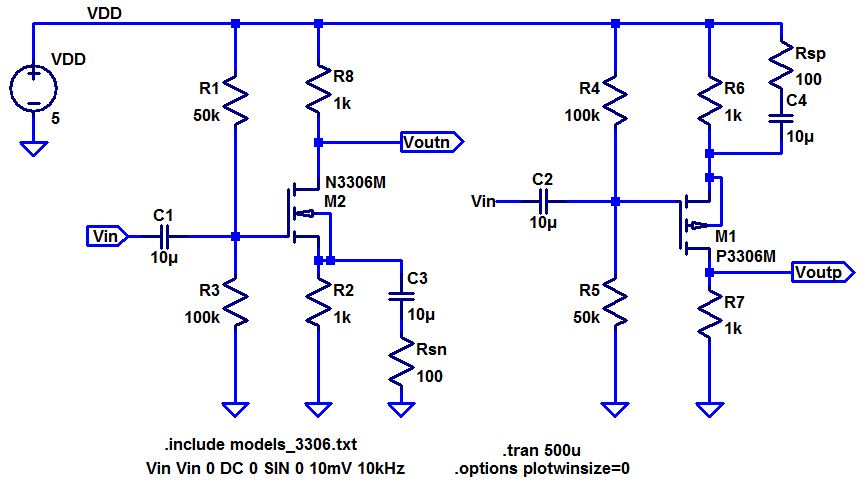
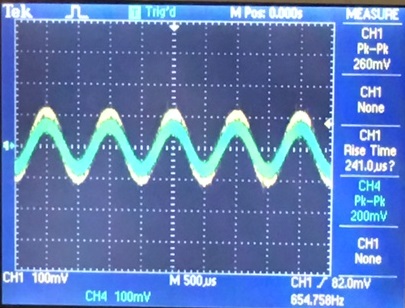
Here we see that the gain for the nmos and pmos circuits is a little less than 1V/V with no phase shift.

Hand calculate, and then verify your hand calculations with experimentation and simulations, the gains and the input and output resistances ensuring that your test signals are at a high enough frequency that the caps have negligible impedance but not so high that the gain is dropping off.

If you build this circuit using electrolitic capacitors, assuming the input AC signal swings around ground, put the "+" terminal of the cap on the gate of the MOSFET. Please indicate, in your lab report, that you understand why the capacitor is connected this way.

The capacitor is connected to the gate of the mosfet due to the DC voltage becoming much larger than the AC input, the positive terminal of the electrolitic capacitor must be connected to the higher potential voltage.

For the hand calculations we need to know gmn and gmp which can be found with simulations.

NMOS
        Rin = 50k//100k = 33k Ohms
        Rout = 1k//1/gmn where gmn = 18.3 m from the simulation
            Rout = 51.813 Ohms
       Vout/Vin = 1k/(1k+1/gmn) = 0.95 V/V which is about 1

PMOS
        Rin = 100k//50k = 33k Ohms
        Rout = 1k//1/gmp where gmp = 10.7m
            Rout = 85.47 Ohms

        Vout/Vin = 1k / (1k + 1/gmp) = 0.9145 V/V


    For the measured values we have

NMOS
        Vout/Vin = Rx / (1/gm + Rx)
                Where Rx is a load resistance. If we find that the gain becomes 1/2 then we will know that Rx = 1/gm

            From our measured values Vout/Vin = 0.75 when Rx = 30.2

            (Rgm + Rx)0.75 = Rx
                Rgm = (Rx-0.75Rx)/0.75 = 10.0667 Ohms

                gmn = 1/10.0667 = 0.0993 A/V
                        our thoretical value for gmn and measured value is incredibly off. This is likely due to the differences between a real world mosfet and a simulated mosfet, such that the circuit needed a different value for the gate voltage to get a matching value for gmn

            Rout = 9.96 Ohms

PMOS
        Rgmp = (Rx - Vout/Vin (Rx))/Vout/Vin

            Vout/Vin = 0.59 at Rx = 0.91.2 Ohms
                Rgmp = 63.37
                1/gmp = 0.01578 A/V = 15.78 mA/V, which is near our theoretical value for gmp
                Rout = 59.6 Ohms

NMOS

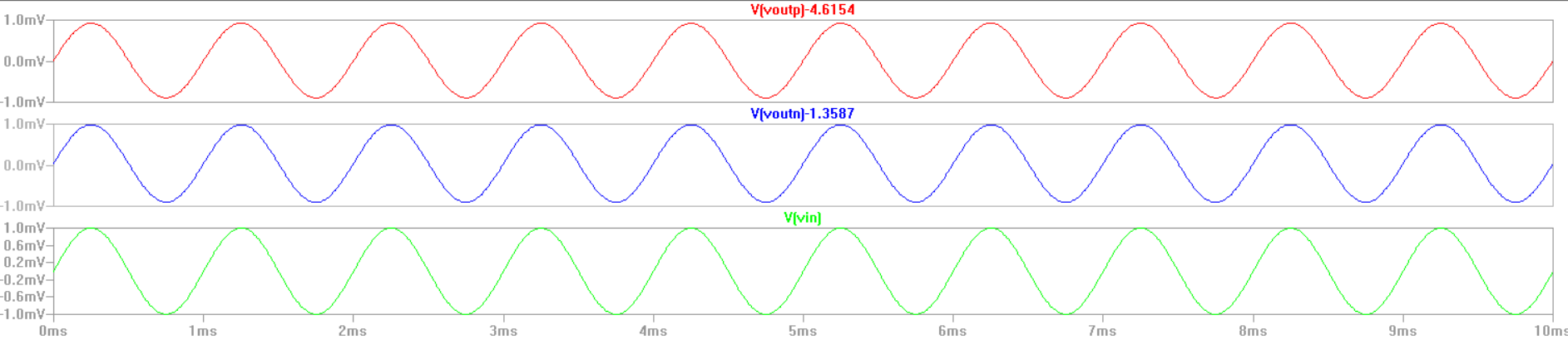
Gain with no load	Gain with load	Input Resistance

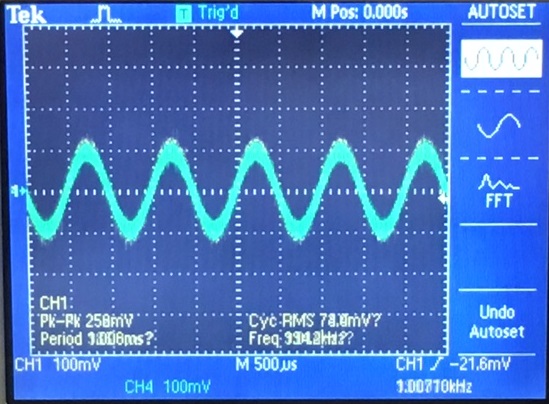PMOS

Gain with no load	Gain with load	Input Resistance

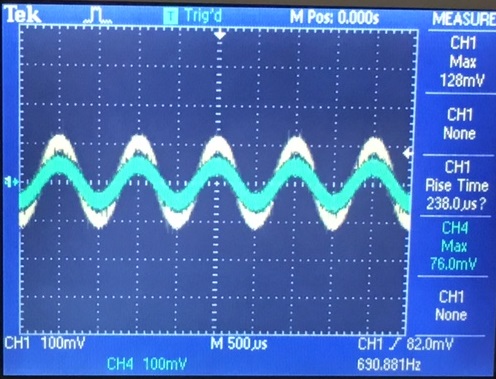In your lab report discuss, in your own words, how to measure the input resistance.

For measuring the input resistance add a resistor equal to the value you calculated between the input voltage source and the amplifier.

Measure the peak AC current through this added resistor by taking the difference in the peak AC voltages across the resistor (on one side is the input voltage signal and the other side is the connection to the amplifier's input capacitor) and then dividing by the resistor's value.

Measure the peak AC voltage on the input of the amplifier (the left side of the capacitor).

Dividing this peak AC voltage by the peak AC current through the added resistor is the amplifier's input resistance.

A multimeter was used to measure the resistance between the gate of the mosfet and ground. With the above measurements we see that Rin in both circuits is about 34k Ohms, which nearly matches the calculated value of Rin of 33k Ohms.

Again, in your lab report discuss how to measure the output resistance.

For measuring the output resistance, add a resistor equal to the value you calculated in series with a big capacitor (to avoid messing up the biasing) from the amplifiers output to ground.

Measure the peak AC current through this added resistor.

Measure the peak AC voltage (remove the DC component) on the gate of MOSFET and the peak AC voltage on the source of the MOSFET. The difference in these two AC voltages is the peak AC gate-source voltage of the MOSFET.

Dividing this peak AC gate-source voltage by the peak AC current through the added resistor is the amplifier's output resistance.

With the above calculations Rx was the test resistance used to measure the Rout, by using the difference with gain we are able to calculate the unknown value for Rout by using the known values of the gain and test resistance.

Below are two common-source amplifiers.

Discuss the operation of these amplifiers in your lab report including both DC and AC operation.

The common source amplifiers function a lot like an op-amp with the inverting topology. The gain for these ampliferes is dependant on the resistor on the drain terminal of the mosfet RD, and the parallel combination of the two resistors connected to the source terminal Rss//Rs. The gain equation for these circuits is Vout/Vin = -Rd/(1/gm + Rss//Rs). Notice that the gain will be negative for a common source amplifer, which is why its function is comparable to an op-amp with an inverting topology.

Hand calculate the gains and the input/output resistances.

How does the source resistance, Rsn or Rsp, influence the gain.

    Rsn and Rsp are in a relate to the gain in

           Vout/Vin = -Rd/(1/gm + Rss//Rs)

    So large values for Rs will become negligible as the parallel combinations will replace large Rs values with Rss, however if Rs is smaller than Rss then Rss will become negligible and Rs will have a larger effect on the gain. So for high gain it is better to set Rs to be as small as possible.

For the hand calculations we have

NMOS

    Vout/Vin = -Rd/(1/gm + Rss//Rs) = -1k / (1/18.3m + (1k//100) = -6.87 V/V
    Rout = Rd = 1k Ohms
    Rin = 50k//100k = 33k Ohms

PMOS

    Vout/Vin = -Rd/(1/gm + Rss//Rs) = -1k / 90.01 + 1/10.7m = -5.423 V/V
    Rout = 1k Ohms
    Rin = 100k//50k = 33k Ohms

Again compare your hand calculations to simulation and experimental results.

For the simulations

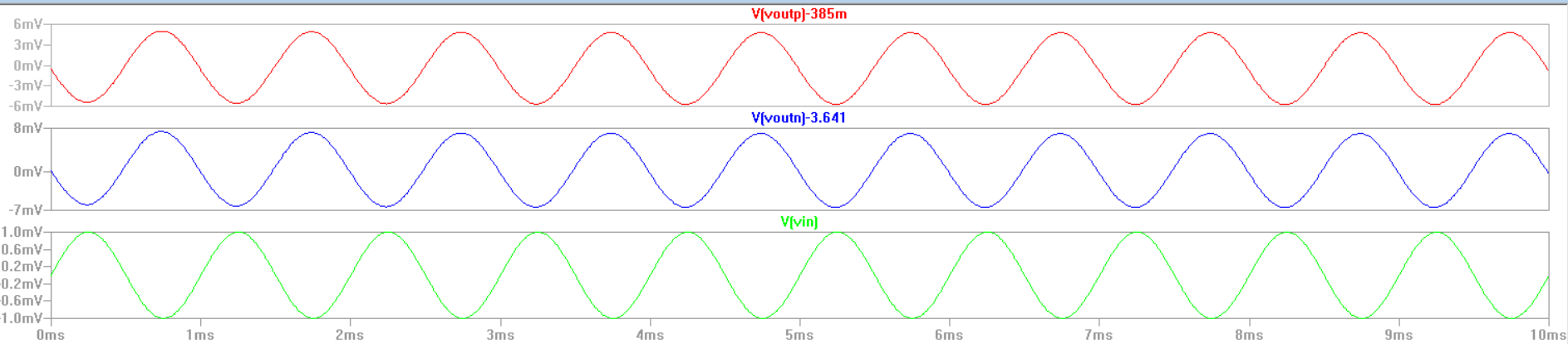
With these simulations we see that a common source amplifer will have an negative gain, for the amplitudes we see that the gain in the nmos is around 7 V/V and for the pmos the gain is about 5 V/V. These simulations closely match the hand calculations

In the measured values we have

NMOS

Gain	Input Resistance	Output Resistance

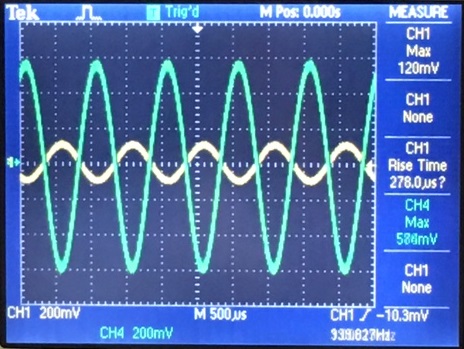Here we see that the gain is 6 V/V with a 180 degree phase shift. Which is off from our theoretical calculation by about 1V.

PMOS

Gain	Input Resistance	Output Resistance

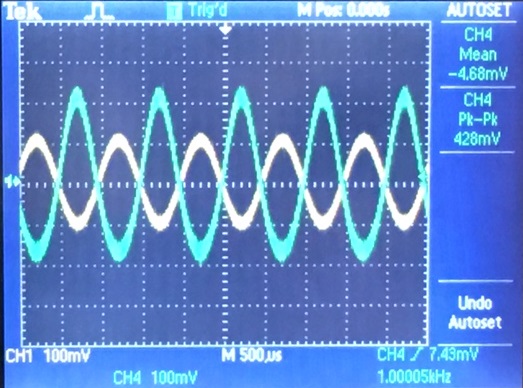Here the gain for the pmos equivalent circuit is about 2 V/V, which is incredibly off of the theoretical value for the gain, this is likely due to incorrect biasing.

Below are two common-gate amplifiers.

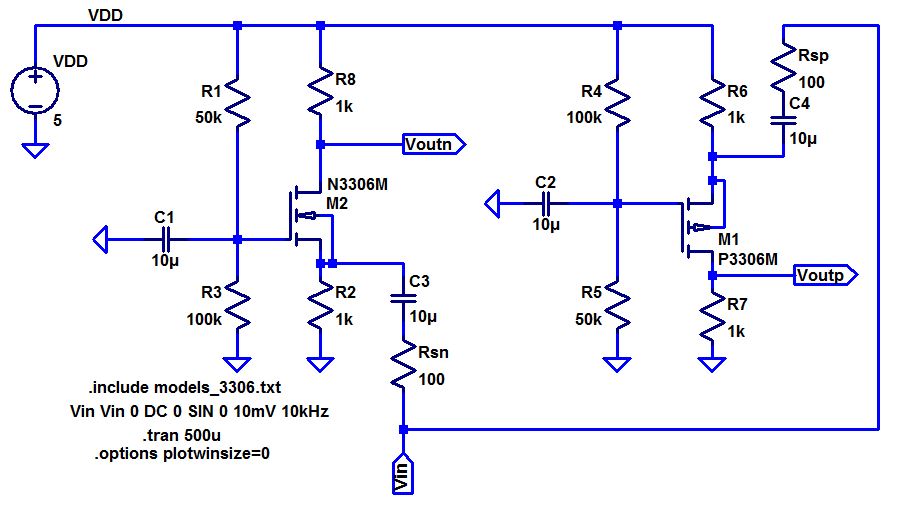
Discuss the operation of these amplifiers in your lab report including both DC and AC operation.

For the common gate amplifier we find that the gain functions simularly with an op-amp that has an non-inverting topology. The gain for these circuit is Vout/Vin = Rd/(1/gm + Rs), which nearly mirrors the gain in the common-source topology, however we can expect the gain to be positive and Rs is no longered influenced by the resistor connected to the source terminal.

Hand calculate the gains and the input/output resistances.

How does the source resistance, Rsn or Rsp, influence the gain.

    For the gain we have Vout/Vin = Rd/(1/gm + Rs), Since Rs is no longer in a parallel combination its size can greatly influence the gain. If Rs is too large we will reduce the size of the gain, to insure that the gain will be high we need to take not that Rd must be larger than Rs.

NMOS

    Vout/Vin = Rd/(1/gm + Rs) = 1k/(100 + 1/18.3m) = 6.466 V/V
    Rout = Rd = 1k Ohms
    Rin = Rs + 1/gm = 154.64 Ohms

PMOS

    Vout/Vin = 1k/(100 + 1/10.7m) = 5.17 V/V
    Rout = 1k Ohms
    Rin = 154.64 Ohms

Again compare your hand calculations to simulation and experimental result

For the simulations we have

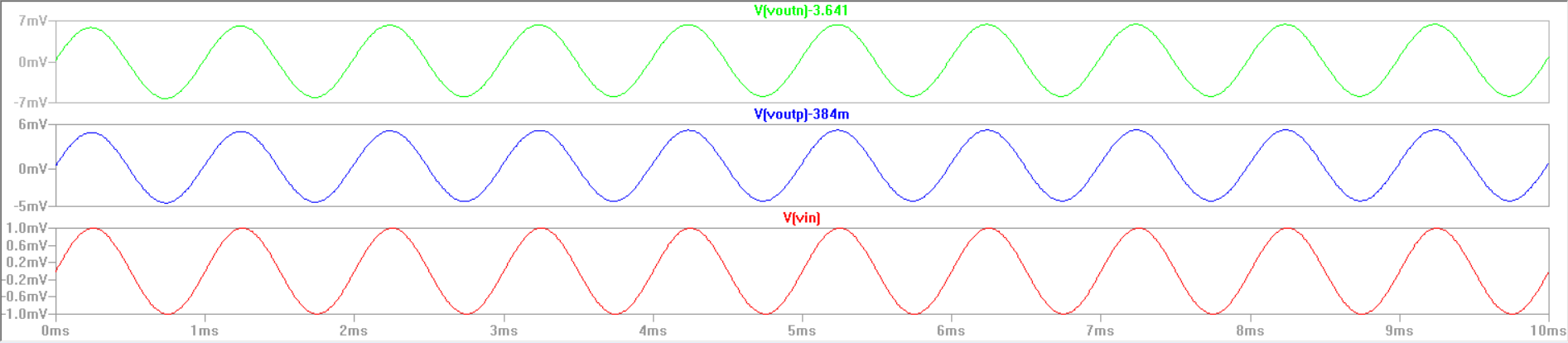
In the Common-Gate case we see that there will be no phase shift. For the nmos the gain is about 6 V/V, and for the pmos we see that the gain is about 5 V/V. These simulated gains do match with our hand calculated gains.

With the measurements we have

NMOS

Gain	Output Resistance

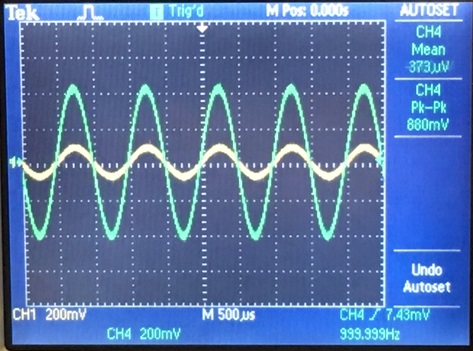PMOS

Gain	Output Resistance

Below is a push-pull amplifier.

Discuss the operation of this amplifier in your lab report including both DC and AC operation.

Hand calculate the gain of this amplifier.

Vout = Rf * (gmp + gmn)*Vin
Vout/Vin = Rf * (gmp + gmn) = 100k (10.7m + 18.3m) = 2900 V/V

Do you expect this amplifier to be good at sourcing/sinking current? Why or why not?

This circuit is good at both sourcing and sinking current. With the PMOS the circuit can source the current, and with the NMOS the current will sink.

What happens to the gain if the 100k resistor is replaced with a 510k resistor? Why?

        We should expect the gain to increase by an factor of 5.1

             Vout/Vin = 510k (10.7m + 18.3m) = 14800 V/V

Again compare your hand calculations to simulation and experimental results.

Note that the gain of this amplifier is large so the output may saturate at VDD and Ground. To avoid this saturation you can reduce the AC input voltage using a voltage divider.

For the simulations we have

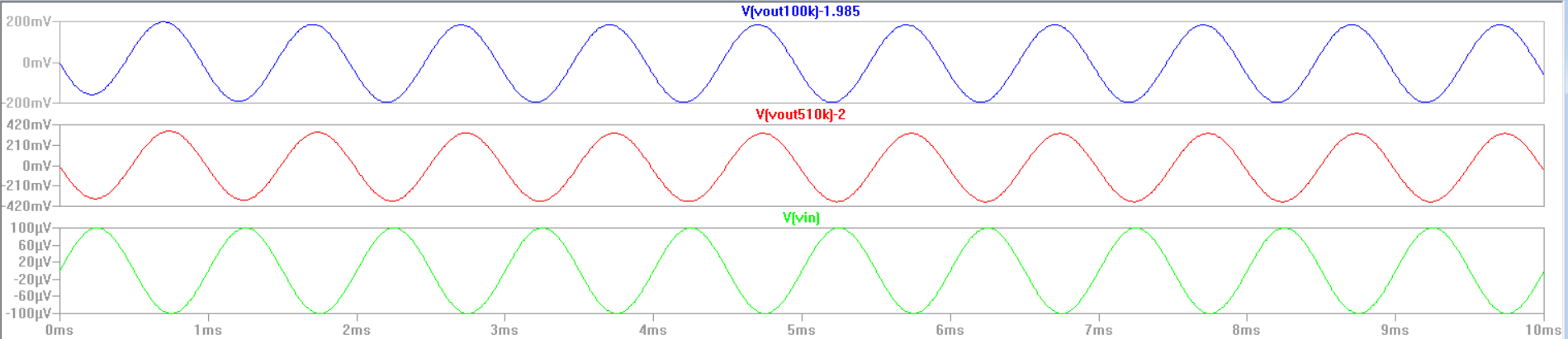
In order to avoid saturation a input voltage of 0.1 mV was used. When Rf=100k we find that the gain is about 2000 V/V , which is lower than our calculated gain. When Rf=510k we see that the gain becomes about 4000 V/V. For the 510k resistor we see that the gain only increased by a factor of 2 and not 5.1, meaning that there is some sort of limit with increasing the gain.

Rf = 100k	Rf = 510k

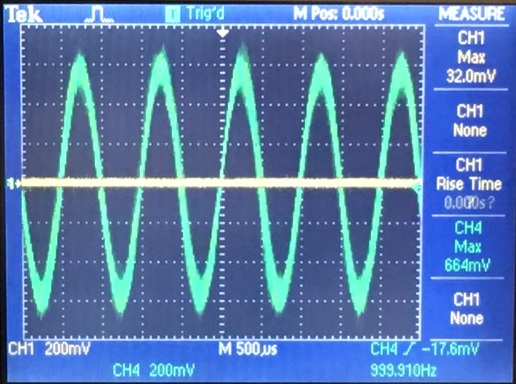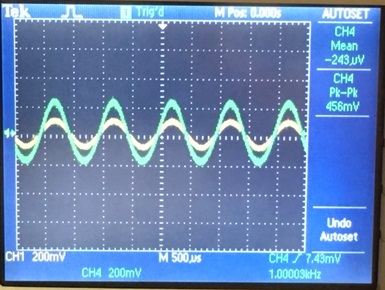
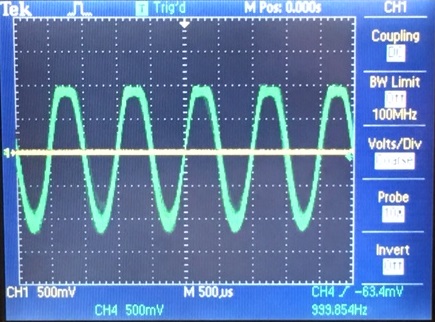
Now we see that the push-pull amplifier is capable of large gains, with Rf = 100k we have a gain of 120 V/V for a 10mV input, this is a lot lower than the hand calculated gains, this is probably due to the limitations of physical mosfets in preforming huge gains. For the 510k case we had saturations when using a 10mV input. At a 1mV input we still see a small amount of amplitude, but the gain here is around 1000 V/V. Though the calculated gain was alot larger we still find that increasing Rf will have a huge effect on gain. Another possibility for why the gain is small with the measured case is that our gm values for the mosfets are smaller than the simulated and calculated cases.

Return