Lab

Lab 5 - EE420L

Authored by Rodolfo Gutierrez

gutie284@unlv.nevada.edu

3/4/2016

Op-amps III, the op-amp integrator

Calculate the frequency response of the following circuit. Ensure you show your clear hand calculations.

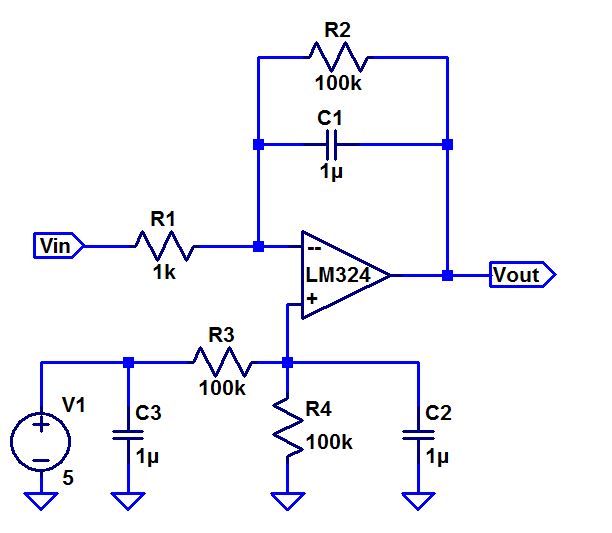
    (Vin - 0)/R1 = (0 - Vout)/C1
    C1/R1 = -Vout/Vin
    C1 = 1/jwC
    Vout/Vin = -1 *(-j)/wRC

    Vout/Vin = j/wRC = 1/ 2*pi*1k*1u = 159.15 Hz

    With the +j we can state that the gain leads by 90 degrees

What can you neglect to simplify the calculation?

Since frequency response requires AC signals we can ignore the 2.5 V entering Vp. The 100k resistor can also be ignored due to it being large enough to block AC current flow.

Does the circuit work if you remove the 100k? Why or why not?

In an ideal scenario the circuit would work, however in the real world you would have a DC offset, so the 100k resistor is there to compensate the offset.

Does the 100k have much of an effect on the frequency response?

No because the resistance is too large for AC current to flow through. In comparison the 1u capacitor is closer to a short circuit.

Verify your calculations with experimental results.

Show, at the unity-gain frequency of the integrator, that the input and the output have the same peak values.

Is the phase shift between the input and the output what you expect? Why or why not?

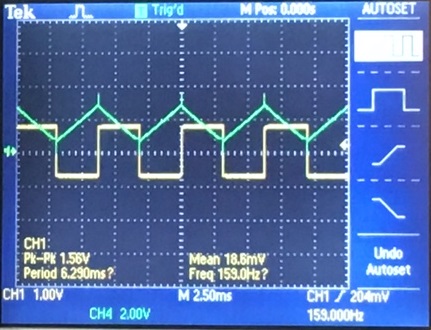
We see that we get a triangular output for our square input at 159 Hz, confirming our calculations for unity gain frequency.We see that the output is leading the input by 90 degrees, which we should expect from the +j term in the frequency response.

Next, design, simulate, and build a square-wave to triangle wave generation circuit.
Assume the input/output frequency is 10 kHz and the output ramp must swing from 1 to 4 V centered around 2.5 V.
Show all calculations and discuss the trade-offs (capacitor and resistor values, input peak, min, and average, etc.)

Vout = T*Vin / 2RC

4 -1 = 2.5*(1/10k) /2RC

RC = 2.5/10k /6 = 41.667 u

Next we can decide either the resistor value or capacitor values. Since it would be easier to acquire unique sized resistors, it would be simpiler to choose the capacitor size

R = 41.667 u / C

We see that if C = 1u, then we will have to use a 41.667 sized resistor. We would rather use a smaller capacitor to get a larger resistor. At C = 0.01u R = 4166.7 Ohms

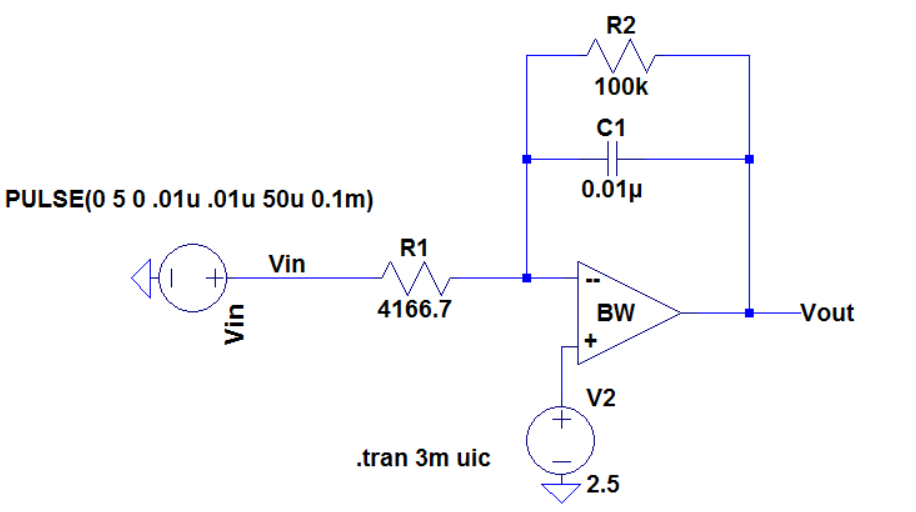
Next we simulate the circuit with our calculated values for R and C, this is to insure that we will get a triangular output that falls within the given constraints.

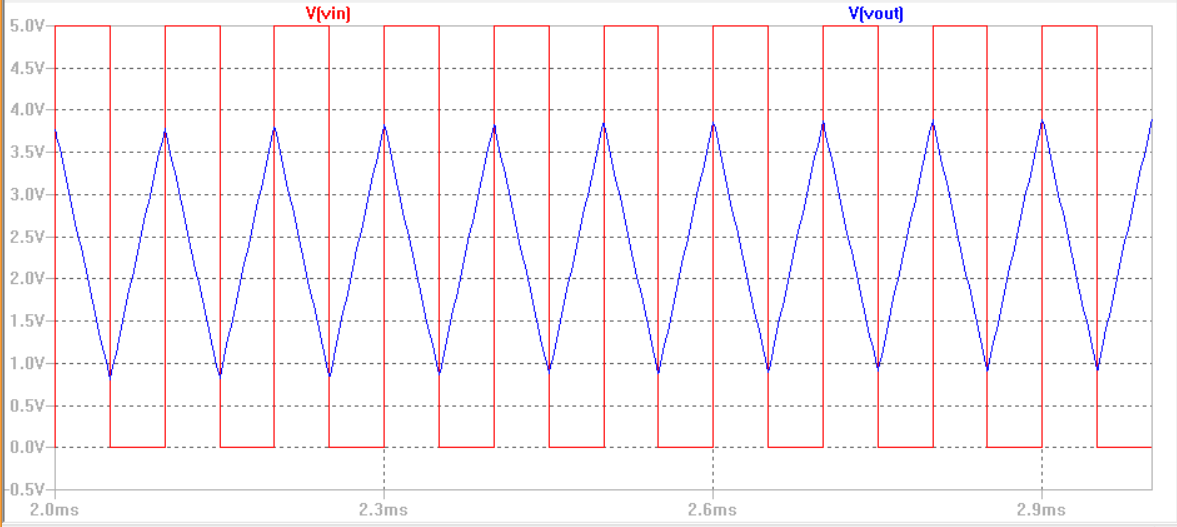
Here we see that our Vout meets the given requirements.

In the lab experiment we see a output waveform that nearly matches our experimental results

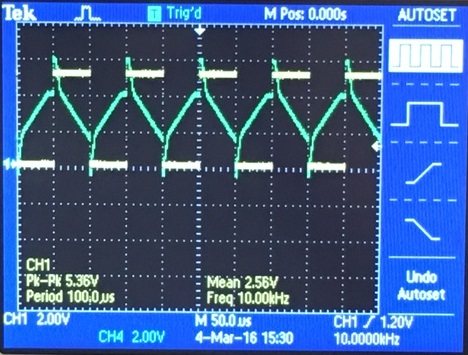
Here at 10kHz we get a triangle output, centered at 2.5 volts. Now the reason why the tips of the triangle wave spike up is because we are using a small capacitor, if the capacitor was larger we would have smoother triangle edges, as seen with the intergrator output seen in the first experiment. Sofor the trade-off between the resistor and capacitor is that if the capacitor is too small we will have larger edge spikes in our intergrator. However if the capacitor is too big we would need to use small resistors to compensate the RC size. We would try improving the design by using a 1k resistor with a 41.667 nF capacitor, although obtaining that capacitor in the lab would require combining smaller capacitors together, we should see an improvment in our output signal.