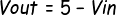Lab 3 - ECE 420L
Authored
by Silvestre Solano,
Email: Solanos3@unlv.nevada.edu
2-20-2015
For the following questions and
experiments assume VCC+ = +5V and VCC- = 0V. The LM324 Op-amp was used for the majority of this lab.
Knowing
the non-inverting input, Vp, is at the same potential as the inverting
input, Vm, (called the common-mode voltage, VCM) what are the maximum
and
minimum allowable common-mode voltages?
In
an ideal op-amp, the output of the op amp is Vout = Aol(Vp-Vm), were
Aol = infinity. In this case, the inputs can be any value as long as
they are zero. However, a real op-amp has a finite power supply that
limits its output, which means that the inputs can only be as high as
the supply voltages. For this op amp, the supply voltages range from
+16 to -16 volts, which means that the maximum input voltage is
16-(-16) = 32 Volts and the minimum is about 16-16 = 0 volts.
Support your
answer with an entry from the electrical characteristics table in the
datasheet.

As,
shown in the above picture, the maximum input voltage is +32 volts and
the minimum is -0.3 volts. This is very close to what I estimated
previously.
What
is a good estimate for the op-amp's open-loop gain?
Support your answer with a
plot from the datasheet and an entry from the electrical
characteristics table.
I
estimate that the open loop gain is about 100000. In the first page of
the datasheet, it state that the gain is about 100dB


What is a good estimate for the offset
voltage?
For worst case design what value would
you use?
I
would estimate a 100 mV offset, even though the datasheet says it has a
max offset of 5mV. For the worst case scenario, I would use my value of
100 mV.
Build,
and test, the following circuit. Note that a precise value for the 5k
resistors isn't important. You can use 4.7k or a 5.1k
resistors.

What is the common-mode voltage, VCM? Does VCM change? Why
or why not?
The VCM is determined as follows:

The measured Vm, Vp and Vout are shown below.
Vm

Vp

Vout

The
VCM in this circuit does not change because there is no current that
flows through the Vp terminal, at least in the ideal model. However,
there is apparantely some kind of bias input current of approximately
20 nA, but the current is very small and negligable. If the input
changes, Vm is affected as a result, but the Vp (VCM) should not
change at all.
What is the ideal closed-loop gain?
From the experiment, the Vout appears to be about 2.5 volts, therefore the ideal closed-loop gain is just Vin/Vout = 2.5/2.5 = 1
What is the output swing and what is it centered around?
The output swing is limited by the power supply given to the op-amp chip. For this circuit, VCC+
= +5V and VCC- = 0V. This means that the op-amp cannot have a Vout
exceeding 5 volts or going below 0 volts. The output swing is centered
around the midpoint between 0 and 5 volts, which is just 2.5
What
happens if the input isn't centered around around VCM, that is, 2.5
V?
Provide a detailed
discussion illustrating that you understand what is going on.
Using KCL, the Vout is derived as follows with Vm = VCM = 2.5 Volts


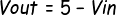
If
the input is changed from 2.5 volts, then the Vout will be changed. For
example, if Vin is changed to 3 volts, then the Vout should change to
about 2 Volts. This was done in lab and the Vout is shown below. The
Vout is not exactly at 2 Volts, but the op-amp is not perfect, so the
slight inaccuracy is expected.
Vin=3 Volts, Vout = 2 Volts.

When
the input is changed to 4 Volts, the output should decrease to 1 Volt.
In the below picture, this appears to be the case. Like the previous
picture, the output voltage vout is not exactly at 1 Volt, but intstead
it appears as 808 mV.
Vin = 4 Volts, Vout = 1 Volt.

The
above results seem to indicate that the ideal op-amp model seems fairly
reliable in determining the characteristics of a real op-amp. The ideal
op-amp model was primarily used to determine the Vp and Vm. Since Vm is
held at a approximate 2.5 Volts, Vp must also be at about 2.5 volts.
However, when the Vin is changed, the Vm remains constant at about 2.5
Volts. This means that the current through Rf must increase or decrease
depending on the Vin. but Vm stays unchanged.
What is the maximum allowable input signal amplitude? Why?
The
maximum allowable input is about 5 Volts. This is because Vout = 5-Vin
and if Vin goes above 5 volts, say 5.5 volts, then the output Vout goes
down to -0.5 volts. This is imposible since the power supply only allow
a maximum output of 5 volts and a minimum output of 0 volts.
What is the maximum allowable input signal if the magnitude
of the gain is increased to 10? Why?
The
maximum allowable input remains the same as in the previous question,
which is 5 volts. This is because the gain is increased, but the supply
voltages remain the same and they limit the maximum output to 5 volts
and minimum output to 0 volts. If the supply voltages are increased,
then the input could go past 5 volts.
What is the point of the 0.01 uF capacitors from VCC and
VCM to ground?
Are these values critical or could 0.1 uF, 1,000 pF, 1
uF, etc. capacitors be used?
The
capacitors used in the circuit are not vital, but instead are used as
so-called decoupling capacitors. They are there to hold the voltage
steady by charging and staying at a given voltage. C1 charges to 2.5
volts and remains at that voltage. C2 charges and remains at 5 volts.
Their
values choosen are not critical at could be any value listed in the
question. I myself used 0.1 uF capacitors instead of the apparently
very popular 0.01 uF.
The data sheet shows that this op-amp has an input bias
current that flows out of the op-amp's inputs of typically 20 nA.
This current flows out of both the non-inverting and
inverting inputs through the resistors connected to these inputs.
Show how the operation of the circuit can be effected if,
for example, R1 and R2, are much larger. Explain what is going on.
If
R1 and R2 are much larger, then they will reduce the current created by
VCC and the small bias current will dominate, creating a small
voltage with the large R2 resistor. For my experiment, the R2 and R1
resistors were at 2 Mega Ohms. The picture below shows this small
voltage captured.

What is the input offset current? What does this term
describe?
The
input offset current is analogous to the offset voltage. It essentially
describes imperfections in the current produced by the op-amp.
This imperfection is modeled as an extra unwanted current.
Explain how the
following circuit can be used to measure the op-amp's offset voltage.
Note that if the output voltage is precisely the same as
VCM then the op-amp has no offset voltage (this is very possible).
To measure small offset voltages increase the gain by
increasing RF to 100k or larger. Explain what is going on.

The
circuit shown above can be used to measure offset voltage by realizing
that ideally no current flows through Rf because (VCM-Vm)/1K =
(VCM-VCM)/1K = 0 amps. With
this information, the following relationship is derived assuming Vm =
VCM+Voff, where Voff is the offset voltage, which could be either
positive or negative.

Using Vm = VCM+Voff arranging terms leads to the following equation.

The
above equation shows that determining the offset voltage is fairly
simple knowing VCM is about 2.5 volts. In order to get more accurate
results, Rf must be increased so that it reduces any leakage current or
the input bias current to prevent it from significantly affecting the
results of the Vout measurement.
Measure the offset voltage of 4 different op-amps and
compare them.
For the following measurements, Rf was changed to 200K Ohms and Voff was calculated using Voff=Vout-VCM.
| LM324 |
| VCM | Vout |
 |  |
| Voff calculated = 1.28 volts |
| LM741 |
| VCM | Vout |
 |  |
| Voff calculated = 0.44 Volts |
| TL082 |
| VCM | Vout |
 |  |
| Voff calculated = -1.08 Volts |
| LF351 |
| VCM | Vout |
 |  |
| Voff calculated = 1 Volt |
As always, I will back up my stuff as shown below.

Return to the main Lab directory.