Lab 4 - EE 420L

Authored by Shada Sharif,

sharifs@unlv.nevada.edu

27 February 2015 

Pre-lab work:

• Watch the video by Dr. Baker.
• Read Lab 4 procedure before going to lab.

• The lab is about understanding the operations of op-amps. Knowing the gain-bandwidth product, and slewing rate. Understanding how high frequencies can affect the circuit. As well as being able to read specifications from the datasheet and verify them experimentally. 

• Estimates about non-inverting bandwidths that are proved using the datasheet.
• Verifying the estimates experimentally.
• Repeat previous steps for inverting op-amp.
• Designing two circuits that measure slew-rate of LM324.pdf.

• The first experiment was a simple one about finding the bandwidths of the non-inverting op-amp configuration for different gains. This was done using the datasheet of the LM324 op-amp.The gains were 1, 5, and 10. 

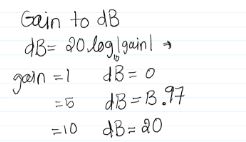
• From the attached picture above we see that the graph is frequency in hertz vs. gain in decibels. So for the gain of 1V/V which is shown as 0dB voltage gain in the open loop frequency response, the bandwidth is around 1.0 MHz. For 5 V/V, which is ~13.9 dB the bandwidth is ~500 kHz. Moreover, for the non-inverting gain of 10V/V which is 20dB, the bandwidth is ~100 kHz. 
• Another way to find the bandwidth is we know that at 0dB the bandwidth is ~1MHz which is also equal to the gain-bandwidth product (since gain-bandwidth product is gain*bandwidth so at 0dB gain =1 and bandwidth is =1MHz; thus gain-bandwidth product is 1*1MHz=1MHz). Using this gain-bandwidth product and dividing it by the gain we desire, the result is the bandwidth. For example, 1MHz/5=200kHz or 1MHz/10=100kHz. Notice how these values are smaller than the ones obtained from the graph. This is because as seen on the open-loop frequency response graph the response of frequencies and their associated gain is for a Vcc = 30V. So different Vcc the bandwidth varies a bit, which we shall see in the next experiment.

• The second experiment is verifying the bandwidths found with the associated gain from experiment #1. A non-inverting op-amp was constructed as shown below with a VCM of 2.5V. V+ of 5V and V- of 0V, and a function generator was used to vary the frequency until the desired gain is reached on the scope. 

   

 
 

• Notice how the 3dB frequencies measured about in the spice waveform simulation match the bandwidths found in experiment #1.
• Hand calculation above show the chosen resistors for this experiment in order to get the desired gain. Since this is the non-inverting topology the gain is calculated as 1+(Rf/Ri), as shown above.
• (In the hand calculation, the input AC signal should be 100mV and not 1mV, so that it matches the experiment.)
• In order to find the bandwidth for each gain of the non-inverting op-amp, we measured the output voltage, at the roll-off frequency (3dB), which is 1/sqrt(2)=0.707 of the output. So we varied the frequency until 0.707*Vout is shown on the scope and the frequency at that instance is the bandwidth for the certain gain being tested. For example, in the gain of 1, the output should be 1mV but at 3dB the output would be 0.707*100mV=70mV. So on the scope wave we see that the input is 96mV and 96mV*0.707=67mV which is very close to the value we have (64mV). Notice the frequency at that value is 1MHz, which is like the estimated value of gain 1 in experiment #1. For the gain of 5, the input voltage used was 200mV so the output at 3dB would be 200mV*0.707*5=707mV, and the is close to the value in the scope wave (712mV). The frequency at that output is seen around 100kHz, which is a lot lower than the values estimated in experiment #1, that is again due to the low power supply voltage used in the experiment (5V). If 30V were used, just like how the bandwidth in the datasheet are based on, then the bandwidth experimentally tested would match datasheet better. Lastly, for a gain of 10, the input voltage used is 200mV, so the 3dB output should be around 200mV*10*0.707=1.414V and that is exactly what we have in the waveform shown above. The bandwidth is much lower than the estimated one, also due to the low Vcc used. 
• Though the circuit being tested is a non-inverting circuit, and the output should match the input phase exactly (ideally), here we see a phase present in all experiment, and that could be because of the high frequencies the circuit is operating on, which bring in a phase in the output signal.

• This experiment is just like the second experiment but this time the inverting topology is being used. So a different circuit is constructed for the inverting op-amp, and again the frequency was varied until the desired gain was shown on the scope. 

                                       Inverting with a gain of 1V/V                                       Inverting with a gain of 5V/V                                           Inverting with a gain of 10V/V

 

• This time due to the inverting topology, the bandwidth will be different. This is due to the bandwidth being calculated using the non-inverting topology. So if the gain is -1 then |-1|*BW=1MHz => BW=1MHz, if we are doing gain of one the Rf and Ri resistor should be the same value so that Rf/Ri=1. Using the noninverting gain equation to find bandwidth => |1+(Rf/Ri)|*BW=10MHz so if gain is 1 => |1+1|*BW=1MHz ==> BW=500kHz. This bandwidth is half that of the bandwidth for the non-inverting topology. Showing how the bandwidth for inverting op-amps is different. As we increase the gain the bandwidth reaches 1MHz more. 
• Notice in the spice simulations, just as explained earlier the 3db frequencies are smaller than the ones for the non-inverting op-amp.
• From the waveforms above, for a gain of 1, the input is 200mV and the output at 3dB is 0.707*(-1)*200mV=-141mV. The frequency is 650kHz and just as discussed earlier a lot smaller than 1MHz due to the way gain-bandwidth product is calculated. For a gain of 5, the input is again 200mV so the output at roll-off frequency is 200mV*(-5)*0.707=-707mV. The frequency is 87kHz, which is smaller than the non-inverting bandwidth at a gain of 5. For a gain of 10, the input used is 200mV, so the 3dB output is 200mV*(-10)*0.707=1.414V. The frequency at that output is 39kHz, not much smaller than that of the non-inverting. 
• Since the Vcc used is 5V, the frequencies are also smaller than what the data-sheet lists them to be. If a high Vcc is used, then the values become more similar and match the datasheet better.

• The last experiment was about finding the slew rate of two circuits we designed, once using a sine wave as an input, and once using a square wave. Slew rate is V/s, and it is a measurement of the maximum rate at which the op-amp can react to a sudden change of input. 

•  From the calculation above, one can see that in order to increase slew rate we can either increase the frequency or increase the amplitude. 
• The circuit used to test slew rate is the same one used in experiment #3. This circuit was used for both a sine wave input and a pulse input by just changing the function feature on the function generator. We used the inverting circuit with a gain of 10 so that the output and change can be seen better on the scope. In order to measure the maximum slew rate, we increased the amplitude but due to the limitation of the op-amp between 0~5V and to avoid quick saturation, we increased the Vcc to 0~15V. 
• In the datasheet picture shown above, the slew rate of the LM324 is 0.4 V/µs. In order to measure slew rate on the scope, we used the measuring feature and measured the peak to peak voltage value and the rise time and to get SR we divided (pk-pk)/(rise time).
• The process we did was varying the amplitude and frequency by increasing the values until the output wave is seen to become saturated and limited by the slew rate of the op-amp.
• As shown in the scope waveforms of the sine wave, when the input is 184mV due to the gain the output is 1.29V. The measure rise time is 265.2 ns. So the slew rate is 184mV/265.2ns=0.694M V/s but we can rewrite it as 0.69V/µs, and that result is not too close to the one provided from the data sheet which could be because each op-amp can have a slightly different slew rate because it is hard to match op-amps exactly. 
• For the square wave input, the same process was done and the same circuit was used. This time the input was 452mV and output was 724mV. This rise time is 876.1ns. Thus the slew rate is 452 mV/876.1 ns=0.515M V/s => 0.5V/µs. Also here the slew rate does not match the one provided by the data-sheet exactly. 

Return